Mann-Kendall検定 ( MATLABコード付き )

最終更新：2021/12/10

Mann-Kendall検定 ( MATLABコード付き ) . 研究室でやけにMann-Kendall検定についてきかれるので, コードをまとめておく. 導出もいつか書きたい.

非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

理論

帰無仮説

データを $(x_1, x_2, \ldots, x_n)$ とするとき,

$H_0$：データ $(x_1, x_2, \ldots, x_n)$ が独立に同じ分布 $F$ に従う.

記号を用いて書くと, $x_1, \ldots, x_n \overset{iid}{\sim} F$ となる. 「トレンドがない」のような, トレンドに明示的に言及した帰無仮説でないことに注意！

検定方法

　 step 1 　
この検定を行うために, まず以下のように $S$ を計算する.

\begin{align} \large S = \sum_{k=1}^{n-1} \sum_{j=k+1}^{n} \text{sgn}(x_j - x_k). \end{align}

なお, ここで $\text{sgn}(x)$ は $x$ の符号 ( $+1, 0, -1$ ) である.

　 step 2 　
つぎに, $V$ を計算する.

\begin{align} \large V &\large= N_s - T_s, \\[10pt] \large N_s &\large= \frac{n(n-1)(2n+5)}{18}, \notag \\[5pt] \large T_s &\large= \sum_{j=1}^{k} \frac{t_j (t_j - 1) (2t_j + 5)}{18}. \notag \\ \end{align}

ここで, $k$ はデータをソートしたときに同じ値が連続して並んだ回数, $t_j$ はそれぞれ連続した個数である. たとえば, $\{5, 3, 1, 3, 5, 3, 5, 4, 3\}$ というデータの場合, ソートすると, $\{1, \color{#cf201f}{3, 3, 3, 3}, 4, \color{#cf201f}{5, 5, 5}\}$ なので, $k = 2$, $t_1 = 4$, $t_2 = 3$ である.

$T_s$ はタイがある場合の取り扱いである. データが実数のときなどは, まずタイが発生することは無いであろう. よって, 以下のコードでは tie = false ( $T_s = 0$ ) をデフォルトしている.

　 step 3 　
最後に, 統計量 $Z$ を計算する.

\begin{align} \large Z = \begin{cases} \frac{S-1}{\sqrt{V}} & S \gt 0, \\[5pt] 0 & S = 0, \\[5pt] \frac{S+1}{\sqrt{V}} & S \lt 0. \\[5pt] \end{cases} \end{align}

これが, 標準正規分布に従うので, その特性を用いて検定を行う.

導出

いつか証明を書く. もし, データが独立同分布からのサンプルなら, $S$ が $0$ に近い値になるのは想像がつくであろう. その特性を用いている.

MATLABコード

コード

MATLAB

function mannkendall(x, alpha, tie)
%MANKENDALL performs a Mann-Kendall test.
% 
%   mannkendall(x, alpha, tie) returns 1 (rejected) or 0 (NOT rejected).
% 
%   x     : Data (1 dim.)
%   alpha : significance level. default : 5%
%   tie   : consider tie (true) or not (false). default : false
% 

% references
% [1] 西岡昌秋, and 宝馨. "Mann-Kendall 検定による水文時系列の傾向変動." 水文・水資源学会誌 17.4 (2004): 343-353.
% [2] https://jp.mathworks.com/matlabcentral/answers/103429-unique

% coded by T.Koshiba, DPRI
% history   09 DEC 2021, v1

if ~exist('alpha', 'var'), alpha = 0.05;  end
if ~exist('tie'  , 'var'), tie   = false; end

N = length(x);
s = 0;
for k = 1:N-1
    for j = k+1:N
        s = s + sign(x(j) - x(k));
    end
end

if tie
    t = sort(s);
    t = arrayfun(@(x)length(find(t == x)), unique(t), 'Uniform', false);
    t = cell2mat(t);
    t = t(t > 1);
else
    t = 0;
end

ns = N * (N-1) * (2*N+5)/18;
ts = sum(t .* (t-1) .* (2*t+5))/18;
v = ns - ts;

if s>0
    z = (s-1)/sqrt(v);
elseif s < 0
    z = (s+1)/sqrt(v);
elseif z == 0
    z = 0;
else
    warning('something is wrong.')
end

p = (1 - normcdf(abs(z), 0, 1));

if p < alpha/2 
    disp("1 (rejected)")
else
    disp("0 (NOT rejected)")
end

end

テスト

適当なデータに使ってみた.

ケース１

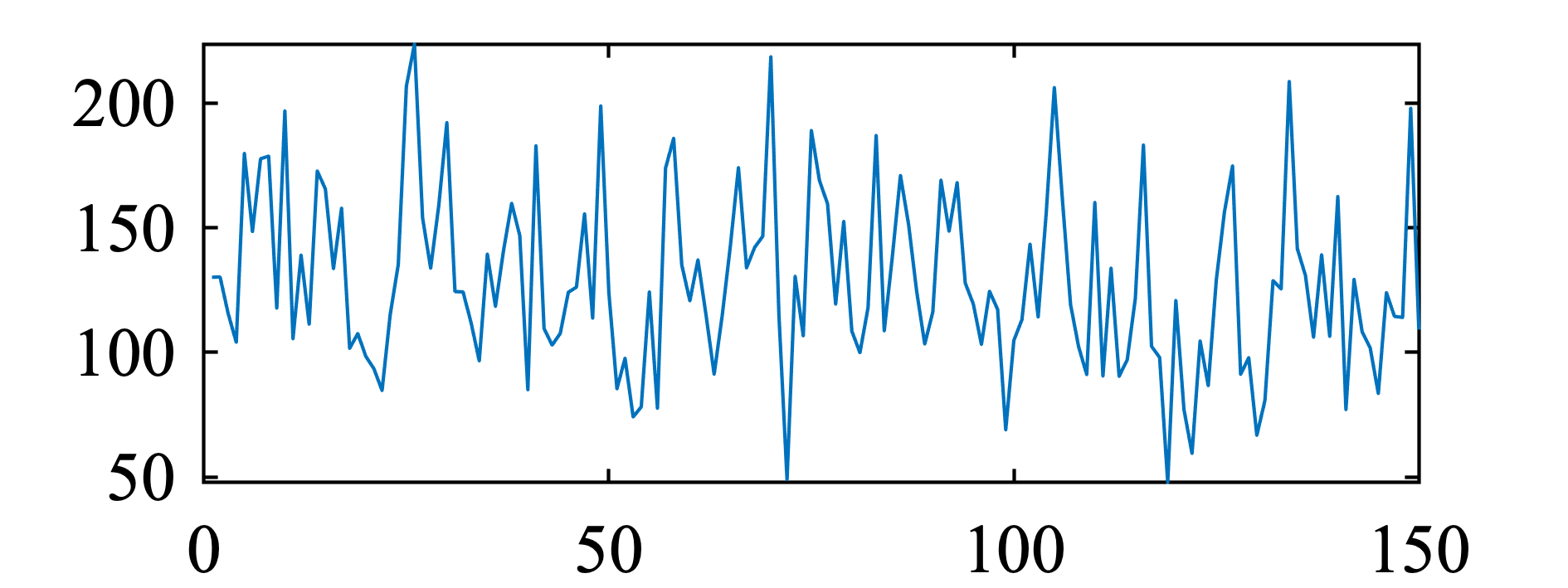
棄却 ( $\text{iid}$ でない ) .

ケース２

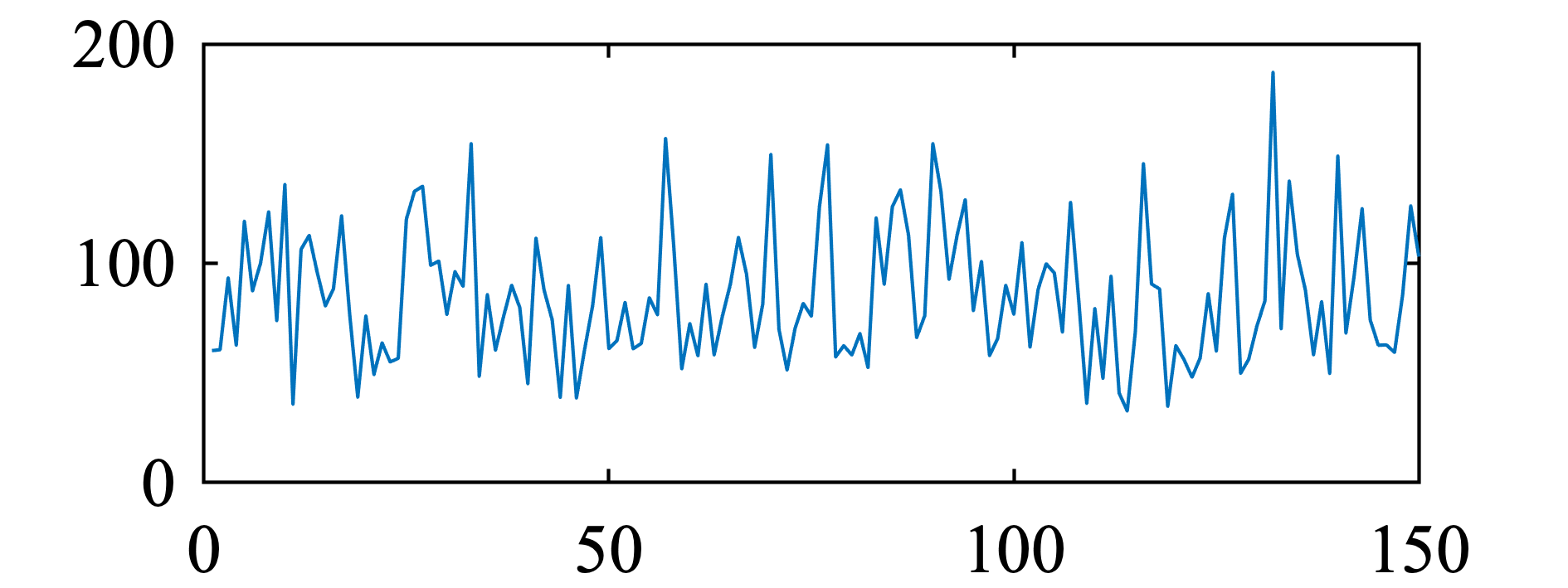
棄却されず ( 何もいえない ) .

ケース３

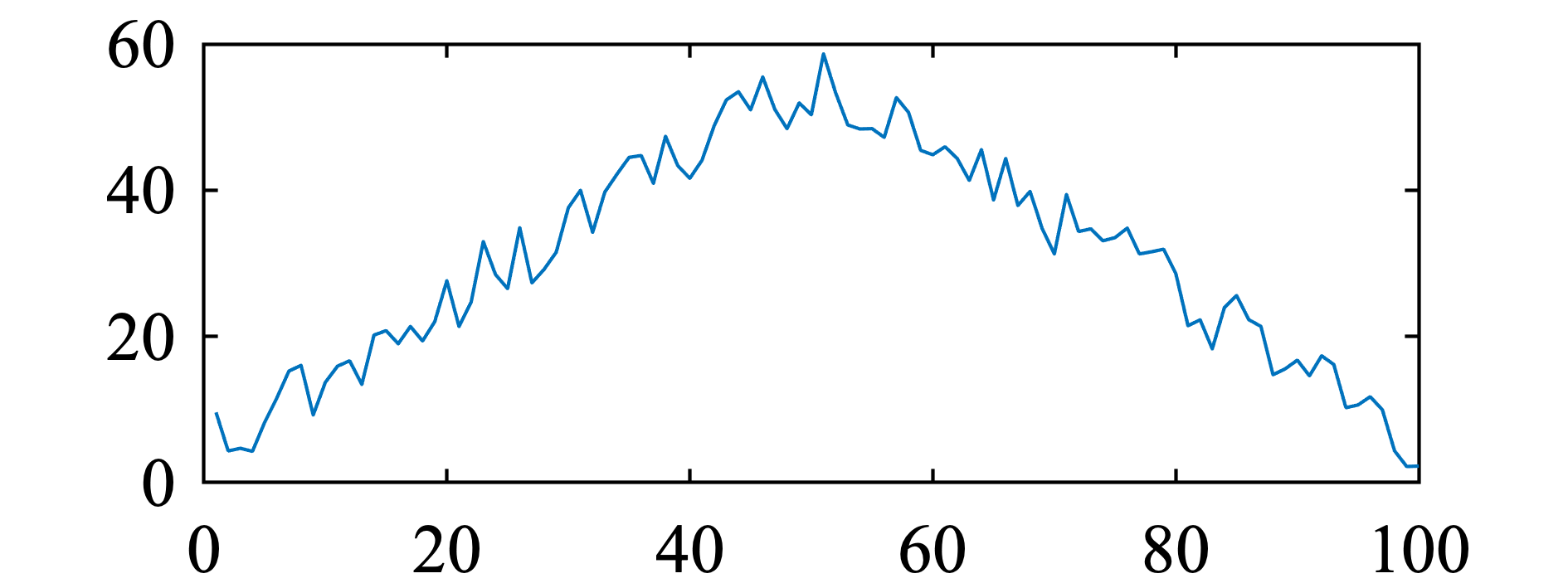
棄却されず ( 何もいえない ) . Mann-Kendall検定は, このようにどうみても $\text{iid}$ でなくても, トレンドが複数あるときなどには, 何も教えてくれないことがあることに注意.

感想・参考文献

参考文献

西岡昌秋, and 宝馨. "Mann-Kendall 検定による水文時系列の傾向変動." 水文・水資源学会誌 17.4 (2004): 343-353.
https://jp.mathworks.com/matlabcentral/answers/103429-unique

この記事のTOP BACK TOP