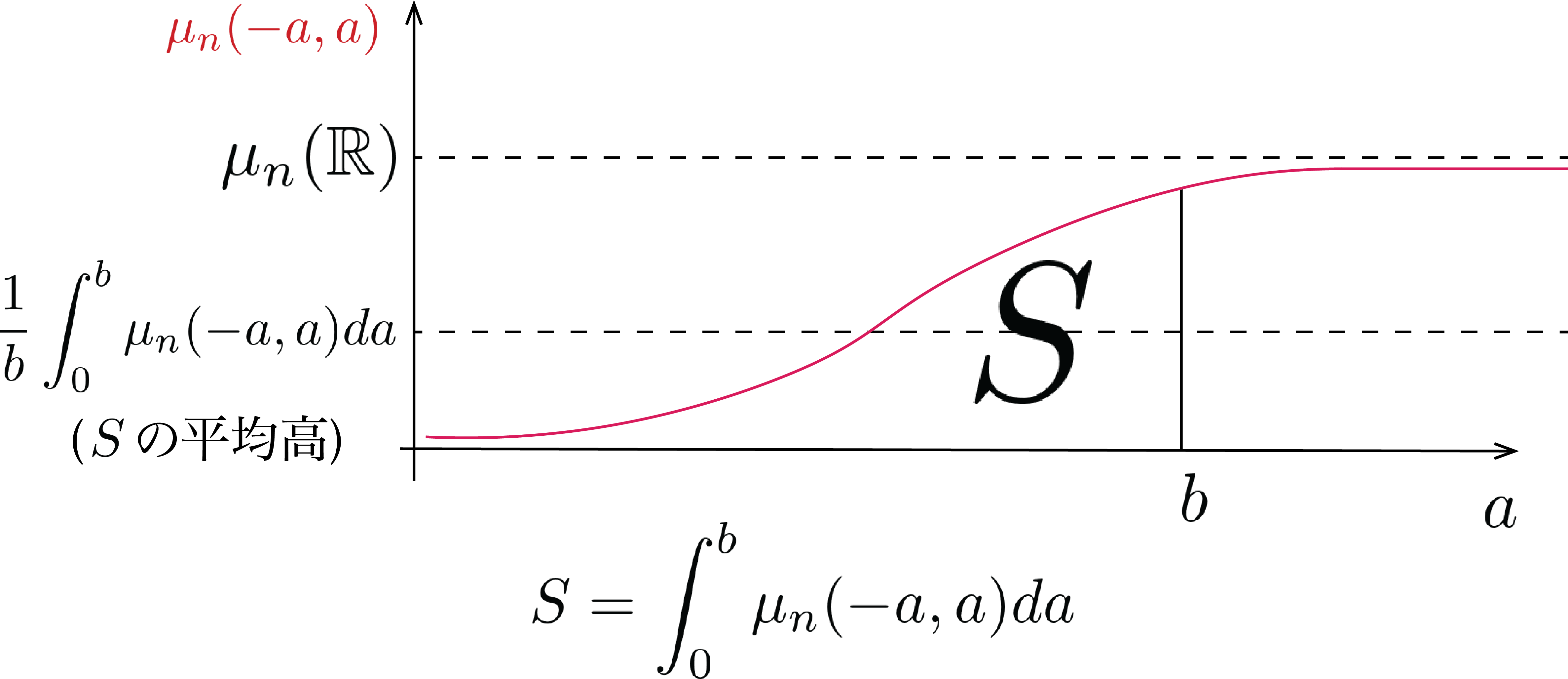Bochnerの定理 ( ボホナーの定理, 伊藤『確率論』定理2.19 ) の証明.
ある函数が特性函数となるための必要十分条件を与える.
Wikipediaによると, 結構厳しい ( 確認し辛い ) 条件であるらしく, これを直接使うことは少ないらしい.
証明
$\Longrightarrow$
必要性は難しくない. 正定性だけ示す.
\begin{align}
&\; \sum_{j, k = 1}^{n} \xi_j \cc{\xi_k} \varphi(z_j - z_k) \\[5pt]
=&\; \sum_{j, k} \xi_j \cc{\xi_k} \int_{-\infty}^{\infty} e^{i(z_j - z_k)x} \mu(dx) \qquad (\because \text{特性函数の定義}) \notag \\[5pt]
=&\; \int_{-\infty}^{\infty} \sum_{j, k} \xi_j \cc{\xi_k} e^{i z_j x} \cc{e^{i z_k x}} \mu(dx) \qquad \notag \\[5pt]
=&\; \int_{-\infty}^{\infty} \sum_{j, k} (\xi_j e^{i z_j x}) (\cc{\xi_k e^{i z_k x}}) \mu(dx) \qquad \notag \\[5pt]
=&\; \int_{-\infty}^{\infty} \left| \sum_{j} \xi_j e^{i z_j x} \right| ^2 \mu(dx) \geq 0. \qquad \notag \\[5pt]
\end{align}
よって, $\varphi$ は正定である.
$\Longleftarrow$
十分性を示そう. B.1, B.2, B.3 が成立するとする.
$\varphi$ は正定なので,
\begin{align}
& \sum_{j, k = 1}^{n} \xi_j \cc{\xi_k} \varphi(z_j - z_k) \geq 0, \notag \\[8pt]
& n = 1, 2, \ldots, \quad \xi_1, \ldots, \xi_n \in \mathbb{C}, \quad z_1, \ldots, z_n \in \mathbb{R}. \notag
\end{align}
である. 変数 $\xi$, $z$ は任意なので, これらに色々な値を代入することで, $\varphi$ の性質を明らかにしていく.
- $n=2$, $\xi_1 = \xi_2 = 1$, $z_1 = z$, $z_2 = 0$ のとき.
これらを, $\sum_{j, k = 1}^{2} \xi_j \cc{\xi_k} \varphi(z_j - z_k) \geq 0$ に代入して,
\begin{align}
2 \varphi(0) + \varphi(z) + \varphi(-z) \geq 0.
\end{align}
いま, 仮定B.3より, $2 \varphi(0) \in \mathbb{R}$ なので, $\varphi(z) + \varphi(-z) \in \mathbb{R}$.
- $n=2$, $\xi_1 = i$, $\xi_2 = 1$, $z_1 = z$, $z_2 = 0$ のとき.
\begin{align}
2 \varphi(0) + i \varphi(z) - i \varphi(-z) \geq 0.
\end{align}
いま, 仮定B.3より, $2 \varphi(0) \in \mathbb{R}$ なので, $i (\varphi(z) - \varphi(-z)) \in \mathbb{R}$.
よって, $\varphi(z) - \varphi(-z)$ は純虚数.
ここまででわかったことを用いると,
$\varphi(z) + \varphi(-z)$ は純実数 $\Rightarrow \varphi(z) + \varphi(-z) = \cc{\varphi(z)} + \cc{\varphi(-z)}$
$\varphi(z) - \varphi(-z)$ は純虚数 $\Rightarrow \varphi(z) - \varphi(-z) = - \cc{\varphi(z)} + \cc{\varphi(-z)}$
であり, 右辺を辺々たし合わせて2で割ると,
\begin{align}
\varphi(-z) = \cc{\varphi(z)}
\end{align}
が得られる.
- $n=2$, $\xi_1 = \xi$, $\xi_2 = \eta$, $z_1 = z$, $z_2 = 0$ のとき.
\begin{align}
\xi \cc{\xi} + \xi \cc{\eta} \varphi(z) + \cc{\xi} \eta \cc{\varphi(z)} + \eta \cc{\eta} \geq 0.
\end{align}
つまり,
\begin{align}
\begin{bmatrix} \eta & \xi \end{bmatrix}
\begin{bmatrix} 1 & \cc{\varphi} \\ \varphi & 1 \end{bmatrix}
\begin{bmatrix} \cc{\eta} \\ \cc{\xi} \end{bmatrix}
\geq 0.
\end{align}
すなわち, 行列 $\begin{bmatrix} 1 & \cc{\varphi} \\ \varphi & 1 \end{bmatrix}$ は正定で, 行列式 $\geq 0$ なので, $|\varphi(z)|^2 \leq 1$.
よって, $|\varphi(z)| \leq 1$.
これで, $\varphi(z)$ が有界であることがわかった.
- $n=3$, $\xi_1 = \xi$, $\xi_2 = -\xi$, $\xi_3 = \eta$, $z_1 = z$, $z_2 = h$, $z_3 = z + h$ のとき.
$\xi_j \cc{\xi_k} \varphi(z_j - z_k)$ を全て書き出すと,
\begin{align}
\begin{bmatrix}
\xi_1 \cc{\xi_1} \varphi(0) & \xi_1 \cc{\xi_2} \varphi(z_2 - z_1) & \xi_1 \cc{\xi_3} \varphi(z_1 - z_3) \\
\xi_2 \cc{\xi_1} \varphi(z_2 - z_1) & \xi_2 \cc{\xi_2} \varphi(0) & \xi_2 \cc{\xi_3} \varphi(z_2 - z_3) \\
\xi_3 \cc{\xi_1} \varphi(z_3 - z_1) & \xi_3 \cc{\xi_2} \varphi(z_3 - z_2) & \xi_3 \cc{\xi_3} \varphi(0) \\
\end{bmatrix}
\end{align}
となり, $\varphi(0) = 1$, $\varphi(-z) = \cc{\varphi(z)}$ を利用しつつ, 変数を代入し全て足し合わせると
\begin{align}
\xi \cc{\xi} (2 - \varphi(h) - \varphi(-h)) + \xi \cc{\eta} (\cc{\varphi(z+h)} - \cc{\varphi(z)}) + \cc{\xi} \eta (\varphi(z+h) - \varphi(z)) + \eta \cc{\eta} \geq 0.
\end{align}
書きかえると,
\begin{align}
\begin{bmatrix} \eta & \xi \end{bmatrix}
\begin{bmatrix} 1 & \varphi(z+h) - \varphi(z) \\ \cc{\varphi(z+h) - \varphi(z)} & 2 - \varphi(h) - \varphi(-h) \end{bmatrix}
\begin{bmatrix} \cc{\eta} \\ \cc{\xi} \end{bmatrix}
\geq 0.
\end{align}
よって,
$\begin{bmatrix} 1 & \varphi(z+h) - \varphi(z) \\ \cc{\varphi(z+h) - \varphi(z)} & 2 - \varphi(h) - \varphi(-h) \end{bmatrix}$ が正定だとわかり,
\begin{align}
2 - \varphi(h) - \varphi(-h) - |\varphi(z+h) - \varphi(z)|^2 \geq 0
\end{align}
が成り立つので,
\begin{align}
|\varphi(z+h) - \varphi(z)|^2 & \leq 2 - \varphi(h) - \varphi(-h) \\[5pt]
& = 2 - \varphi(h) - \cc{\varphi(h)} \notag \\[5pt]
& = 2 (1 - \Re{\varphi(h)}) \notag \qquad (\Re \text{は実部})\\[5pt]
& = 2 \Re{(1 - \varphi(h))} \notag \\[5pt]
& \leq 2 |1 - \varphi(h)|. \notag
\end{align}
これと, $\varphi$ は $z = 0$ で連続であることとから, $\varphi$ は一様連続だとわかる.
証明 ( click )
$\varphi(0) = 1$, $\varphi$ は $z = 0$ で連続なので,
\begin{align}
\lim_{h \to 0} \varphi(h) = 1.
\end{align}
よって,
\begin{align}
\lim_{h \to 0} |\varphi(z + h) - \varphi(z)| \leq 2 |1 - \varphi(0)| = 0 \Longrightarrow \lim_{h \to 0} \varphi(z+h) = \varphi(z).
\end{align}
これが任意の $z$ に対して成り立つ, つまり,
\begin{align}
& {}^\forall \ve \gt 0, \; {}^\exists \delta = \delta(\ve),\; {}^\forall z \in \mathbb{R}, \\[5pt]
& |h| \leq \delta \Longrightarrow |\varphi(z+h) -\varphi(z)| \lt \ve. \notag
\end{align}
$\square$
ここまでで, $\varphi$ が有界一様連続函数だとわかった.
いま, 連続有界可積分函数 $g$ を含む以下のような式を考える.
\begin{align}
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \varphi(t - s) g(t) \cc{g(s)} dt ds \label{eq1}
\end{align}
この式を, 総和記号を用いて ( 区分求積のように ) 書き直すと,
\begin{align}
\lim_{n \to \infty} \sum_{j, k = n^2}^{n^2} \color{#0033cc}{\varphi \left( \frac{j}{n} - \frac{k}{n} \right) g \left( \frac{j}{n} \right) \cc{g \left( \frac{k}{n} \right)}} \left( \frac{1}{n}\right)^2 \label{eq2}
\end{align}
となる ( 最後の $(1/n)^2$ は各区分の面積である ) .
ここで, $\varphi$ が正定であるという仮定を思い出すと, 青字部分 $\geq 0$ なので, 式\eqref{eq2}全体も $\geq 0$ となり, 当然式\eqref{eq1}も $\geq 0$ となる.
変数を $t - s \to t$, $s \to s$ と変換した式\eqref{eq1}を用いてこの事実を書くと,
\begin{align}
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \varphi(t) g(t + s) \cc{g(s)} dt ds \geq 0
\end{align}
となる. 正値可測函数に対するFubiniの定理 ( 例えば参考文献[3] ) を用いて,
\begin{align}
\int_{-\infty}^{\infty} \varphi(t) \int_{-\infty}^{\infty} g(t + s) \cc{g(s)} ds dt \geq 0 \label{eq3}
\end{align}
とできる. とくに, ガウシアン $\mathcal{N}$ を用いて
\begin{align}
g(t) = \mathcal{N}_{0, n/4}(t) e^{-ixt}
\end{align}
とすると, ガウシアンの性質より以下がなりたつことをふまえて
- $\mathcal{N}_{0, v}(t) = \mathcal{N}_{0, v}(-t)$,
- $\mathcal{N}_{0, \alpha}(t) * \mathcal{N}_{0, \beta}(t) = \mathcal{N}_{0, \alpha+\beta}(t)$,
\begin{align}
\int_{-\infty}^{\infty} g(t+s) \cc{g(s)}ds &= \mathcal{N}_{0, n/4} * \mathcal{N}_{0, n/4} e^{-ixt} \\[5pt]
&= \mathcal{N}_{0, n/4} e^{-ixt} \notag \\[5pt]
&= \sqrt{\frac{1}{\pi n}} e^{-t^2/n} e^{-ixt}. \notag
\end{align}
よって, これを式\eqref{eq3}に戻し, $\sqrt{\frac{1}{\pi n}}$ が正であることをふまえて
\begin{align}
\int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} e^{-ixt} dt \geq 0,
\end{align}
が得られる. いま, 左辺に $(2 \pi) ^{-1}$ をかけることで以下のように函数 $f_n$ を定義する.
\begin{align}
f_n(x) := \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} e^{-ixt} dt.
\end{align}
さらに, $f_n$ を用いて
\begin{align}
\mu_n(dx) := f_n(x) dx
\end{align}
を定義すると, $\mu_n$ が分布を定めることを示そう.
まず, $\mu_n$ は $\cB$ 上の測度となる.
証明 ( click )
$\mu_n \geq 0$ 自明.
$A_n \in \cB$ のとき,
\begin{align}
\mu_n \left( \bigsqcup_{n=1}^\infty A_n \right) &= \int_{\sqcup A_n} f_n(x) dx \\[5pt]
&\color{#cf201f}{=} \sum_{n=1}^{\infty} \int_{A_n} f_n(x) dx \notag \\[5pt]
&= \sum_{n=1}^{\infty} \mu_n (A_n) \notag \\[5pt]
\end{align}
なお, $\bigsqcup$ は直和.
また, 等号 $\color{#cf201f}{=}$ は, 例えば, 吉田ルベグp.171など参照.
$\square$
よって, 残るは $\mu_n(\mathbb{R}) = 1$ を示せば良い.
\begin{align}
\mu_n(-a, a) &= \frac{1}{2 \pi} \int_{-a}^a f_n(x) dx \\[5pt]
&= \frac{1}{2 \pi} \int_{-a}^a \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} e^{-itx} dt dx \notag \\[5pt]
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \int_{-a}^a e^{-itx} dx dt \notag \qquad \because \text{Fubini}\\[5pt]
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \frac{2 \sin{at}}{t} dt \notag \\[5pt].
\end{align}
ここで, $a \to \infty$ で $\mu_n(-a, a) \uparrow \mu_n(\mathbb{R})$ なので,
\begin{align}
\mu_n(\mathbb{R}) = \lim_{b \to \infty} \frac{1}{b}\int_0^b \mu_n(-a, a) da \label{eq4}
\end{align}
とかくことができる.
これは, 以下の図のように考えるとわかりやすい.
$\mu_n(-a, a)$ は, すでにのべたように, $\mu_n(\mathbb{R})$ に下から漸近する函数で, $\int_0^b \mu_n(-a, a) da$ が面積 $S$ である.
すると, $\lim_{b \to \infty} \frac{1}{b}\int_0^b \mu_n(-a, a) da$ は, 領域 $S$ の平均高さであるが, これは, $b$ を大きくすることで, いくらでも $\mu_n(\mathbb{R})$ に近づけることができる.
いま, 式\eqref{eq4}に $\mu_n(dx) = f_n(x)dx$ を戻すと,
\begin{align}
\mu_n(\mathbb{R}) &= \lim_{b \to \infty} \frac{1}{b} \int_0^b \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \frac{2 \sin{at}}{t} dt da \\[5pt]
&= \lim_{b \to \infty} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \int_0^b \frac{2 \sin{at}}{bt} da dt \qquad \because \text{Fubini} \notag \\[5pt]
&= \lim_{b \to \infty} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \frac{2(1 - \cos{bt})}{bt^2} dt \notag \\[5pt]
&= \lim_{b \to \infty} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi\left( \frac{t}{b} \right) e^{-t^2/nb^2} \frac{2(1 - \cos{t})}{t^2} dt \notag \\[5pt]
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \lim_{b \to \infty} \varphi\left( \frac{t}{b} \right) e^{-t^2/nb^2} \frac{2(1 - \cos{t})}{t^2} dt \qquad \because \text{有界収束定理} \notag \\[5pt]
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(0) \frac{2(1 - \cos{t})}{t^2} dt \notag \\[5pt]
&= \frac{1}{\pi} \varphi(0) \color{#cf201f}{\int_{-\infty}^{\infty} \frac{1 - \cos{t}}{t^2} dt}. \notag \\[5pt]
\end{align}
となり, 赤字の積分が $\pi$ になることを使うと ( 岩波公式集など参照 ) ,
\begin{align}
\mu_n{(\mathbb{R})} = \varphi(0) = 1
\end{align}
となる.
これで, $\mu_n$ が分布であることがいえた.
ここまでで, $\varphi$ を用いて分布列 $\mu_n$ を作ることができた.
次に, $\mu_n$ の特性函数 $\varphi_n(z)$ を計算してみよう.
\begin{align}
\varphi_n(z) &= \int_{-\infty}^{\infty} e^{izx} f_n(x) dx \\[5pt]
&= \lim_{a \to \infty} \int_{-a}^a e^{izx} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} e^{itx} dt dx \notag \\[5pt]
&= \lim_{a \to \infty} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \int_{-a}^a e^{i(t+z)x} dx dt \qquad \because \text{Fubini} \notag \\[5pt]
&= \lim_{a \to \infty} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \frac{2 \sin{a(t-z)}}{t-z} dt \notag \\[5pt]
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \lim_{a \to \infty} \frac{2 \sin{a(t-z)}}{t-z} dt. \qquad \because \text{有界収束定理} \notag \\[5pt]
\end{align}
ここで,
\begin{align}
\lim_{a \to \infty} \frac{2 \sin{a(t-z)}}{t-z} dt \notag
\end{align}
について, 前図で説明した内容と同様に,
\begin{align}
\lim_{b \to \infty} \frac{1}{b} \int_0^b \frac{2 \sin{a(t-z)}}{t-z} da \notag
\end{align}
と書き換えて,
\begin{align}
\varphi_n(z) &= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \lim_{b \to \infty} \frac{1}{b} \int_0^b \frac{2 \sin{a(t-z)}}{t-z} da dt \\[5pt]
&= \lim_{b \to \infty} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(t) e^{-t^2/n} \frac{2(1 - \cos{b(t-z)})}{b(t-z)^2} dt \qquad \because \text{有界収束定理} \notag \\[5pt]
&= \lim_{b \to \infty} \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi\left( z + \frac{s}{b} \right) e^{-(z + s/b)^2/n} \frac{2(1 - \cos(s))}{s^2} ds \notag \\[5pt]
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \lim_{b \to \infty} \varphi\left( z + \frac{s}{b} \right) e^{-(z + s/b)^2/n} \frac{2(1 - \cos(s))}{s^2} ds \qquad \because \text{有界収束定理} \notag \\[5pt]
&= \frac{1}{2 \pi} \int_{-\infty}^{\infty} \varphi(z) e^{z^2/n} \frac{2(1 - \cos(s))}{s^2} ds \notag \\[5pt]
&= \varphi(z) e^{z^2/n} \frac{1}{\pi} \int_{-\infty}^{\infty} \color{#cf201f}{\frac{1 - \cos(s)}{s^2} ds}.
\end{align}
となり, 再び赤字の積分が $\pi$ になることを使うと,
\begin{align}
\varphi_n(z) = \varphi(z) e^{z^2/n}
\end{align}
となる. よって,
\begin{align}
\varphi_n(z) \to \varphi(z) \quad (n \to \infty).
\end{align}
ここまでで, $\mu_n$ の特性函数列が, $\varphi$ に収束するとわかった.
この収束は, 少なくとも $|z| \leq 1$ で一様なので, Lévyの収束定理が使えて, $\varphi$ は或る分布の特性函数である.
$\square$
$\blacksquare$