分布列の収束

最終更新：2021/11/28

分布列の収束の定義と, 同値な命題 ( 伊藤『確率論』定理2.10 ).

非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

定義

分布列 $\{\mu\}$ が $\mu$ に収束するとは, 任意の有界連続実函数 $f$ に対して,

\begin{align} \large \int_{\mathbb{R}^1} f(x) \mu_n(dx) \longrightarrow \int_{\mathbb{R}^1} f(x) \mu(dx) \quad (n \rightarrow \infty) \end{align}

が成立すること. これを,

\begin{align} \mu_n \longrightarrow \mu \end{align}

と記す.

分布の収束と同等な命題 ( 定理2.10 )

以下は同等. ただし, 分布 $\mu_n$, $\mu$ の分布函数を $F_n$, $F$ とする.

$\mu_n \longrightarrow \mu$,
コンパクトな台をもつ任意の連続函数 $g$ に対し,
\begin{align} \large \int_{\mathbb{R}^1} g(x) \mu_n(dx) \longrightarrow \int_{\mathbb{R}^1} g(x) \mu(dx) \quad (n \rightarrow \infty) \end{align}
$E^o$, $\overline{E}$ をそれぞれ $E$ の開核, 閉包とする. このとき, $\mu(E^o) = \mu(\overline{E})$ なる全ての $E$ に対し, $\mu_n(E) \longrightarrow \mu(E)$,
$F$ の全ての連続点にたいして, $F_n(x) \longrightarrow F(x)$,
$\mathbb{R}^1$ で稠密な可算集合 $C$ があって, ${}^\forall x \in C$ に対して, $F_n(x) \longrightarrow F(x)$.

証明

$\mathrm{(iii)} \Rightarrow \mathrm{(iv)} \Rightarrow \mathrm{(v)}$ はあきらかなので, $\mathrm{(v)} \Rightarrow \mathrm{(ii)} \Rightarrow \mathrm{(i)} \Rightarrow \mathrm{(iii)}$ を示す.

$\mathrm{(v)} \Rightarrow \mathrm{(ii)}$

$g$ をコンパクトな台をもつ連続函数とする. すると, $g$ は一様連続.

( $\because$ ) ( click )

例えば, 松坂『集合と位相』6章定理6. $(S, d)$ がコンパクトな距離空間なら, $(S, d)$ から任意の距離空間 $(S', d')$ への連続函数は一様連続.

したがって, ${}^\forall \ve \gt 0$ に対してコンパクトな台をもつ左連続階段函数 $g_\ve(x)$ があって,

\begin{align} \sup_{x} | g_\ve(x) -g(x) | \lt \ve. \end{align}

注意 ( click )

一様連続であるので, $\ve$ という定数で抑えられる. 連続だが, 一様連続でない函数として, 例えば $1/x$ を考えれば $0$ に近いところで $\ve$ の様な定数が取れないことは解るだろう.

また, 仮定 ( v ) の $C$ は稠密 ( 即ち $\overline{C} = \mathbb{R}^1$ ) なので, 階段函数 $g_\ve$ の飛躍点 $a_i = a_i(\ve)$, $(i = 0, 1, \ldots, m, m = m(\ve))$ は全て $C$ に属すると仮定してよい ( もし, $a_i$ が $C$ の点でなくても, $C$ の集積点ではあるので, 上の式を満たすような $C$ の点を限りなく $a_i$ に近づけることで選べなおせる ) .

いま, 簡単のため以下を定める.

\begin{align} (g, \nu) \equiv \int_{\mathbb{R}^1}g(x)\nu(dx). \end{align}

すると,

\begin{align} &\quad |(g, \mu_n) - (g, \mu)| \\[5pt] =&\quad |(g, \mu_n) - (g_\ve, \mu_n) + (g_\ve, \mu_n) - (g_\ve, \mu) + (g_\ve, \mu) - (g, \mu)| \notag \\[5pt] \leq&\quad |(g, \mu_n) - (g_\ve, \mu_n)| + |(g, \mu) - (g_\ve, \mu)| + |(g_\ve, \mu_n) - (g_\ve, \mu)| \notag \\[5pt] \end{align}

ここで, 第１項 ( また第２項も同様に )

\begin{align} \int_{\mathbb{R}^1} (g(x) - g_\ve(x)) \mu_n(dx) \leq \mu_n(\mathbb{R}^1) \sup_x|g(x) - g_\ve(x)| \leq \ve \end{align}

が成り立つ. また, 第３項については,

\begin{align} \left| \sum_{i=1}^m g_\ve(a_i)(F_n(a_i) - F_n(a_{i-1})) - \sum_{i=1}^m g_\ve(a_i)(F(a_i) - F(a_{i-1})) \right| \end{align}

で抑えられる. 一方, 仮定 ( v ) によって, 全ての $i = 0, 1, \ldots, m$ に対して, $\lim_{n \rightarrow \infty}F_n(a_i) = F(a_i)$ なので, 結局上の式は $n \rightarrow \infty$ で $0$ に収束する.

これらをまとめると,

\begin{align} \limsup_{n \rightarrow \infty} |(g, \mu_n) - (g, \mu)| \leq 2 \ve. \end{align}

$\ve$ は任意なので, $n \rightarrow \infty$ で $(g, \mu_n) - (g, \mu) \rightarrow 0$.

$\square$

$\mathrm{(ii)} \Rightarrow \mathrm{(i)}$

$f$ を任意の有界連続実函数とする. ${}^\forall m \gt 0$ に対し, $[-m, m]$ で $f$ と一致し, $[-m-1, m+1]$ の外では $0$ となる連続函数 $g$ を用意する. また, $f-g$ は有界なので, ある定数 $C$ が存在して, $|f(x) - g(x)| \leq C$ となる. この $C$ を用いて, 連続函数 $h(x)$ を

\begin{align} h(x) = \begin{cases} 0 & \mathrm{on\,}[-m+1, m-1], \\[5pt] C & \mathrm{on\,}[-m, m], \\[5pt] 0 \leq h(x) \leq C & \mathrm{otherwise}. \\[5pt] \end{cases} \end{align}

と定義する.

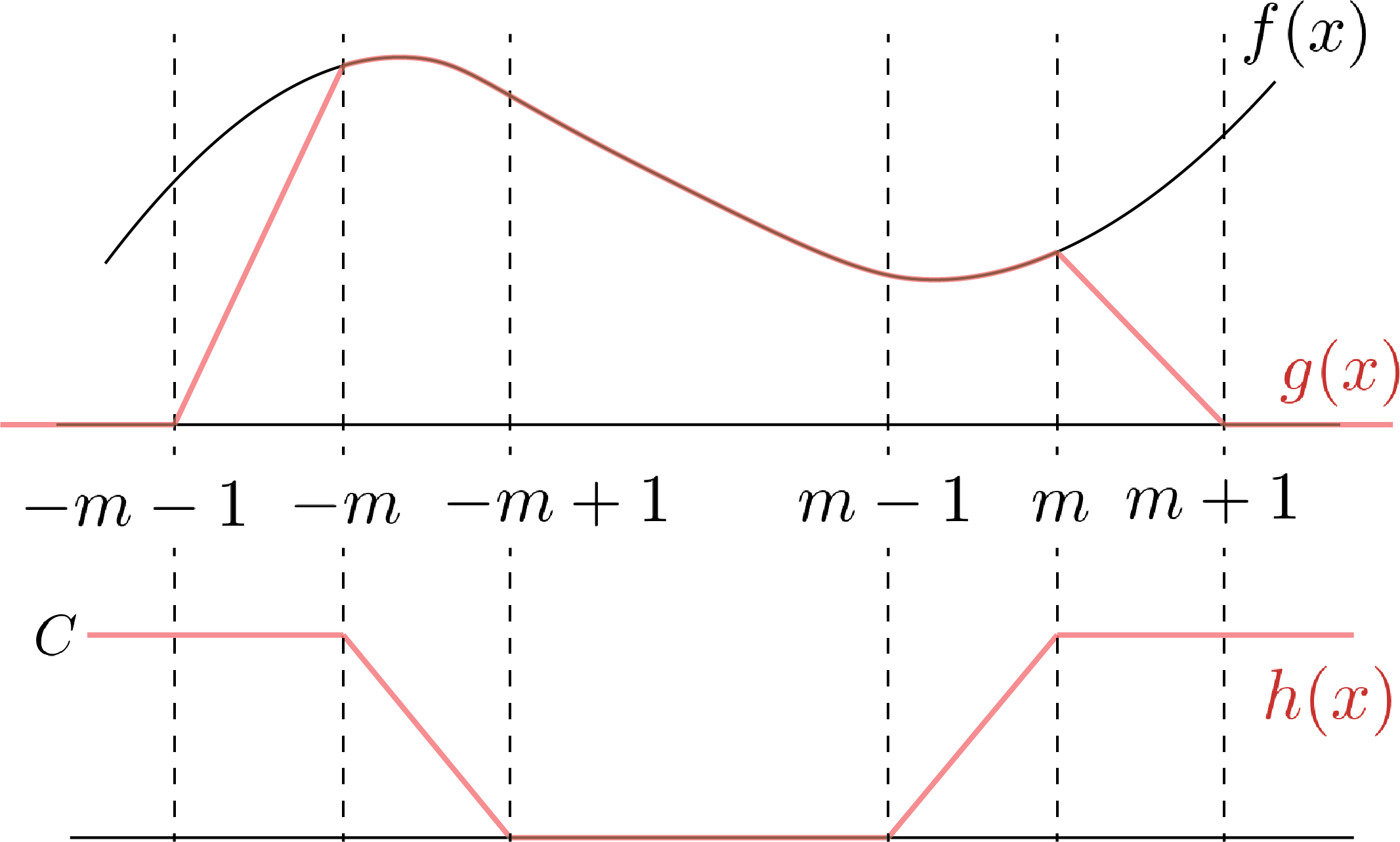
今, 証明のゴールは $|(f, \mu_n) - (f, \mu)|$ が $n \rightarrow \infty$ で $0$ となることである.

\begin{align} &\quad |(f, \mu_n) - (f, \mu)| \label{bb} \\[5pt] = &\quad |(f, \mu_n) - (g, \mu_n) + (g, \mu_n) - (g, \mu) + (g, \mu) - (f, \mu)| \notag \\[5pt] \leq &\quad \color{#cf201f}{(|f-g|, \mu_n)} + \color{#0033cc}{(|f-g|, \mu)} + \color{#006600}{|(g, \mu_n) - (g, \mu)|}. \notag \end{align}

$f - g$ が $[-m, m]$ で $0$ なので ( 上図 ) ,

\begin{align} |f(x) - g(x)| \leq h(x). \end{align}

よって,

\begin{align} &\quad \color{#cf201f}{(|f-g|, \mu_n)} \leq (h, \mu_n) \\[5pt] =&\quad (C, \mu_n) - (C-h, \mu_n) = C - (C - h, \mu_n). \notag \end{align}

$C - h$ は $[-m, m]$ ( コンパクト ) の外では $0$ なので, 仮定 ( ii ) より, 以下がなりたつ.

\begin{align} (C-h, \mu_n) \longrightarrow (C-h, \mu) = C - (h, \mu) \quad (n \rightarrow \infty). \end{align}

よって,

\begin{align} \limsup_{n \rightarrow \infty} \color{#cf201f}{(|f-g|, \mu_n)} \leq (h, \mu) \leq C \mu([-m+1, m-1]^c). \end{align}

また,

\begin{align} \color{#0033cc}{(|f-g|, \mu)} \leq (h, \mu) \leq C \mu([-m+1, m-1]^c). \end{align}

なお上の２式において, $(h, \mu) \leq C \mu([-m+1, m-1]^c)$ である理由は,

\begin{align} (h, \mu) &= \int_{\mathbb{R}^1} h(x)\mu(dx) \\[5pt] &= \int_{[-m+1, m-1]} h(x)\mu(dx) + \int_{[-m+1, m-1]^c} h(x)\mu(dx) \notag \\[5pt] &= 0 + \int_{[-m+1, m-1]^c} h(x)\mu(dx) \notag \\[5pt] &\leq C \mu([-m+1, m-1]^c). \notag \end{align}

さらに, 函数 $g$ はコンパクトな台をもつので, 仮定 ( ii ) より,

\begin{align} \lim_{n \rightarrow \infty} \color{#006600}{|(g, \mu_n) - (g, \mu)|} = 0. \end{align}

ここまでで得られた不等式を式\eqref{bb}に代入すると,

\begin{align} \limsup_{n \rightarrow \infty} |(f, \mu_n) - (f, \mu)| \leq 2C\mu ([-m+1, m-1]^c). \end{align}

右辺は, $m \rightarrow \infty$ で $0$ に収束するので,

\begin{align} (f, \mu_n) \longrightarrow 0 \quad (n \rightarrow \infty). \end{align}

$\square$

$\mathrm{(i)} \Rightarrow \mathrm{(iii)}$

$E$ を条件 ( iii ) を満たす集合とする ( $\mu(E^o) = \mu(\overline{E})$ ) . $\mathbb{R}^1$ の中では,

全ての開集合は増加閉集合の極限,
全ての閉集合は減少開集合の極限

であるから ( 例えば伊藤ルベーグ§4定理3.4 ) , あらゆる $\ve \gt 0$ に対して $F_\ve \subset E^o$ となる閉集合 $F_\ve$ と, $G_\ve \supset \overline{E}$ となる開集合 $G_\ve$ が存在する. すると,

\begin{align} \mu(E^o) - \mu(F_\ve) \lt \ve,\quad \mu(G_\ve) - \mu(\overline{E}) \lt \ve. \end{align}

仮定より, $\mu(E^o) = \mu(\overline{E})=\mu(E)$ なので,

\begin{align} \mu(F_\ve) \gt \mu(E) - \ve,\quad \mu(G_\ve) \lt \mu(E) - \ve. \end{align}

この開集合 $G_\ve$ と閉集合 $\overline{E}$ とに対して連続函数 $f_\ve$ をとって,

\begin{align} f_\ve = \begin{cases} 0 & \mathrm{on\;} G_\ve^c, \\[5pt] 1 & \mathrm{on\;} \overline{E}, \\[5pt] 0 \leq f_\ve \leq 1 & \mathrm{otherwise} \\[5pt] \end{cases} \end{align}

と定義する. すると, 仮定 ( i ) より

\begin{align} \lim_{n \rightarrow \infty} (f_\ve, \mu_n) = (f_\ve, \mu) \\[5pt] \mu_n(E) \leq \mu_n(\overline{E}) \color{#cf201f}{\leq} (f_\ve, \mu_n) \end{align}

不等号 $\color{#cf201f}{\leq}$ が成り立つ理由は, 以下の通り.

\begin{align} (f_\ve, \mu_n) = \int_{\mathbb{R}^1} f_\ve(x) \mu_n(dx) &= \int_{\overline{E}} f_\ve(x)\mu_n(dx) + C,\; C \gt 0 \\[5pt] &= \int_{\overline{E}} 1 \mu_n(dx) + C \notag \\[5pt] &= \mu_n(\overline{E}) + C. \notag \end{align}

よって,

\begin{align} \lim_{n \rightarrow \infty} \mu_n(E) \leq \lim_{n \rightarrow \infty} (f_\ve, \mu_n) = (f_\ve, \mu) \leq \mu(G_\ve) \leq \mu(E) + \ve \label{cc} \\[5pt] \Longrightarrow \limsup_{n \rightarrow \infty} \mu_n(E) \leq \mu(E). \notag \end{align}

同様に, $E^o$ と $F_\ve$ に対して連続函数 $g_\ve$ をとって,

\begin{align} \liminf_{n \rightarrow \infty} \mu_n(E) \geq \mu(E). \end{align}

これで, 式\eqref{cc}と上式とから

\begin{align} \mu_n(E) \longrightarrow \mu(E)\quad (n \rightarrow \infty) \end{align}

がいえた.

$\square$

これで, 条件 ( i ) ~ ( v ) の同値性がいえた.

$\blacksquare$

感想・参考文献

感想

これで, 分布収束を示すときに使えそうな同値な条件が得られた. 結構難しかった.

参考文献

伊藤清確率論 (岩波基礎数学選書)

松坂集合・位相入門

伊藤ルベーグ積分入門(新装版) (数学選書)

この記事のTOP BACK TOP