MATLABで『時系列解析入門』7章の追記
最終更新:2021/06/08
7章 の一部の内容は, コードが複雑になったり, 計算が合わなかったりして不安だったので, 単変量ARモデルと多変量ARモデルを 愚直に正規方程式を解くことで求めてみる.
正規方程式, $\theta = (X^{T}X)^{-1}X^{T}y$, は教科書では精度や計算時間の問題からお薦めされていないが, MATLABではX\yとするだけで
解いてくれるのでそれを用いる.
もちろん, MATLABもバカみたいに逆行列を求めているのではなく, 賢く早い方法で解いてくれているのでその力にあやかる.
アルゴリズム ( mathworks )
のフローチャートを見てもらえばわかるように, 結局QR分解を用いているようである.
非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.
単変量ARモデル
モデルとコード
M次のARモデル
function [aic, Arcoef, s2, maic] = arNormaleq(d, lag)
%ARNORMALEQ
%
% INPUT
% d : data
% lag: maximum AR degree (lag)
%
% OUTPUT
% aic : AIC
% Arcoef : AR coefficient (structure)
% s2 : sigma^2
% maic : The order which provides the minimum AIC
% preprocessing
d = reshape(d, [], 1);
d = d - mean(d);
N = length(d);
% preallocation
s2 = zeros(1, lag);
aic = zeros(1, lag);
% main
for M = 1:lag
X = zeros(N-M, M);
for I = 1:M
X(:, I) = d(M-I+1:N-I);
end
y = d(M+1:N);
theta = X\y;
y_est = X*theta;
s2(M) = sum((y - y_est).^2)/(N-M);
aic(M) = (N-M) * (log(2*pi*s2(M)) + 1) + 2*(M+1);
% save AR coeff
name = ['order' num2str(M)];
Arcoef.(name) = theta;
end
% calculate maic
[~, maic] = min(aic);
end
適用
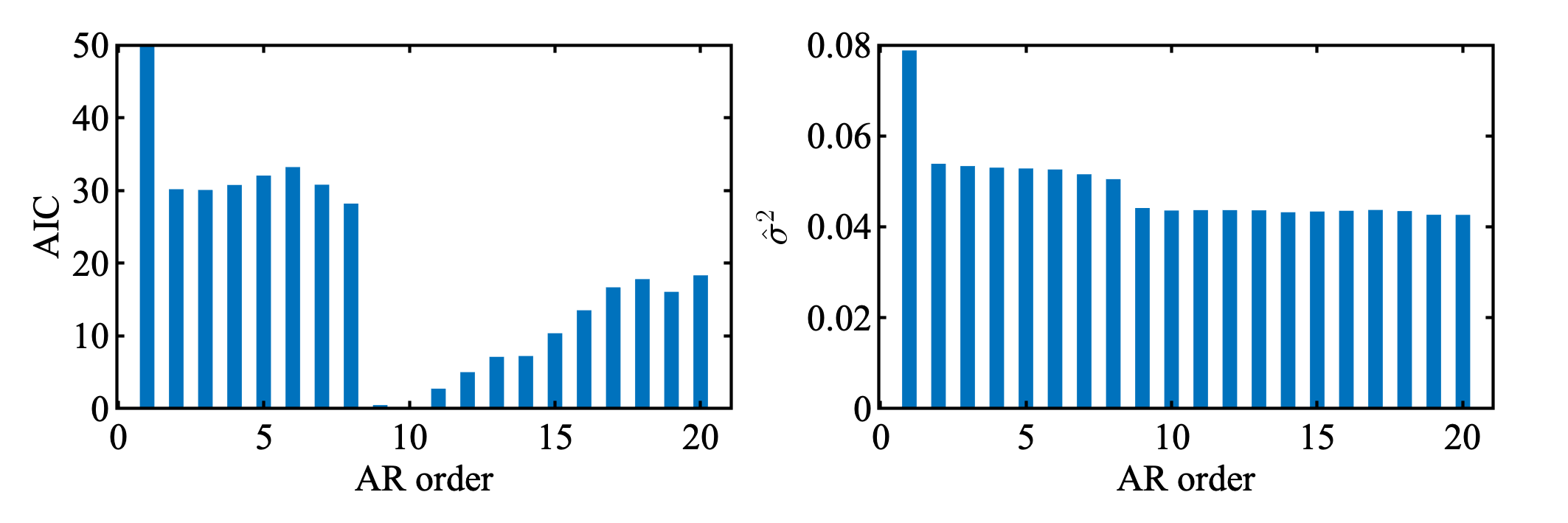
7章 の結果と比較するため太陽黒点数 ( SUNSPOT ) に適用した. ぱっとみ七章の図と違うように見えるのは, 次数0の結果がないから. それ以外はよく合っている.
MATLABコード
MATLAB
d = sunspot;
d(d==0) = 10^0.1;
d = log10(d);
lag = 20;
[aic, Arcoef, s2, maic] = arNormaleq(d, lag); % ここがメイン
% PLOT
t = tiledlayout(1, 2); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
bar(1:lag, aic-min(aic), 0.5, 'LineStyle', 'none')
ylim([0 50]);
xlabel('AR order')
ylabel('AIC')
nexttile
bar(1:lag, s2, 0.5, 'LineStyle', 'none')
xlabel('AR order')
ylabel('$\hat{\sigma}^2$','Interpreter','latex')
多変量ARモデル
モデルとコード
教科書6.7節「多変量ARモデル」より, モデルは
cov(res)で求めた.
function [aic, V, Arcoef, maic] = mvArNormaleq(d, K, lag)
%MVARNORMALEQ
%
% INPUT
% d :data
% k :dimension of the data
% lag :maximum AR degree
%
% OUTPUT
% aic : AIC (size = lag * k)
% Arcoef : AR coefficient
% V : variance-covariance matrix
% maic : The order which provides the minimum AIC
% preprocessing
d = reshape(d, [], K);
d = d - mean(d);
N = size(d, 1);
% preallocation
V = zeros(K, K, lag);
aic = zeros(1, lag);
% main
for M = 1:lag
% make X
X = zeros(N-M, M*K);
for I = 1:M
X(:, K*(I-1)+1:K*I) = d(M-I+1:N-I, :);
end
y = d(M+1:end, :);
theta = X\y; % solve normal equation
res = X*theta - y; % calculate residual
V(:, :, M) = cov(res); % save variance covariance matrix
% save AIC
aic(M) = N * (K*log(2*pi) + log(det(V(:, :, M))) + K) + K*(K+1) + 2*K^2*M;
% save AR coeff
name = ['order' num2str(M)];
Arcoef.(name) = permute(reshape(theta, [K, M, K]), [2, 1, 3]);
end
% calculate maic
[~, maic] = min(aic);
end
適用
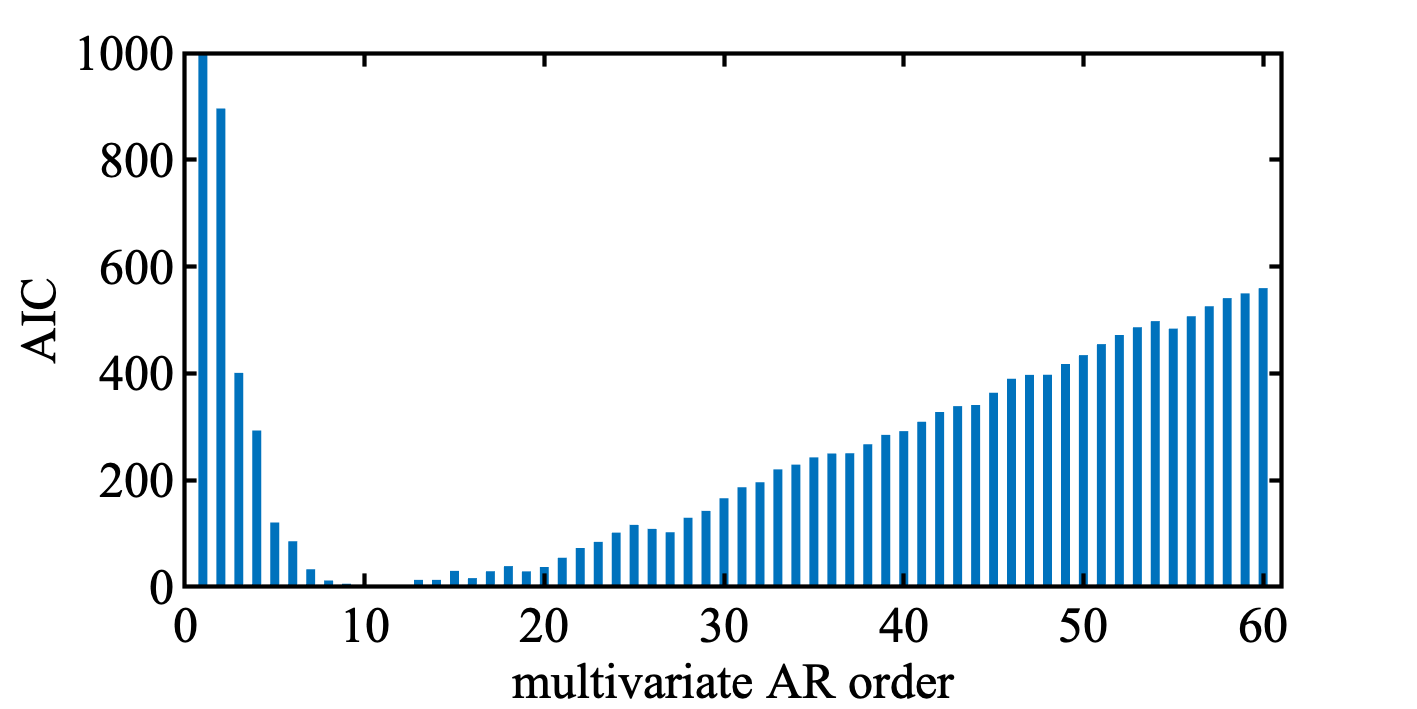
例として, 船舶データ ( HAKUSAN ) に適用してみた. 4変数, 最大次数20でトライ. 正直複雑でコードに自信がないけど, 最小AICを与える次数は10で, 教科書とおなじになった. AICの増加の仕方も直線的でいい感じ.
MATLABコード
MATLAB
d = hakusan.velocity;
d = [d hakusan.tate];
d = [d hakusan.yoko];
d = [d hakusan.dakaku];
K = 4;
lag = 60;
[aic, V, Arcoef, maic] = mvArNormaleq(d, K, lag);
bar(1:lag , aic - min(aic), 0.5, 'LineStyle', 'none');
ylim([0 1000])
ylabel('AIC')
xlabel('multivariate AR order')
パワースペクトル・コヒーレンシー!要再検査!
教科書6.7節「多変量ARモデル」にのっとりパワースペクトル・コヒーレンシーを求める函数を作った. だいたい教科書と合った結果がでるが, ちょっと自信がないので参考程度に.
function [spec, amp, phase, coh, power, rpower, f] = crossSpectrum(arcoef, v)
% CROSSSPECTRUM
%
% INPUTS
% arcoef: AR coeff matrix
% v : variance-covariance matrix of the noise
%
% OUTPUTS
% spec : cross spectrum
% amp : amplitude spectrum
% phase : phase spectrum
% coh : coherency
% power : power spectrum decomposition
% rpower: relative power contribution
% f : frequency
df = 0.001;
f = 0:df:0.5;
N = length(f);
K = size(v, 1);
M = size(arcoef, 1);
% cross spectrum
spec = zeros(K, K, N);
F = zeros(M, N);
for m = 1:M
F(m, :) = exp(-2*pi*1i*m*f);
end
A = zeros(N, K, K);
for k = 1:K
for j = 1:K
for m = 1:M
A(:, j, k) = A(:, j, k) + (arcoef(m, j, k) * F(m, :))';
end
A(:, j, k) = A(:, j, k) -1*(j == k);
end
end
A = permute(A, [2, 3, 1]);
for I = 1:N
spec(:, :, I) = A(:, :, I) \ (v / A(:, :, I)');
end
spec = permute(spec, [3, 1, 2]);
% amplitude and phase spectrum
amp = abs(spec);
phase = angle(spec) + 2*pi;
% coherency
coh = zeros(size(spec));
for k = 1:K
for j = 1:K
coh(:, j, k) = amp(:, j, k).^2 ./ (real(spec(:, j, j)) .* real(spec(:, k, k)));
end
end
% relative power contribution
power = zeros(size(spec));
B = zeros(size(A));
for I = 1:N
B(:, :, I) = inv(A(:, :, I));
end
B = permute(B, [3, 1, 2]);
for k = 1:K
for j = 1:K
power(:, j, k) = v(k, k) * abs(B(:, j, k)).^2;
end
end
rpower = zeros(size(power));
for k = 1:K
sumPower = sum(squeeze(power(:, k, :)), 2);
for j = 1:K
rpower(:, k, j) = sum(squeeze(power(:, k, 1:j)), 2) ./ sumPower;
end
end
end
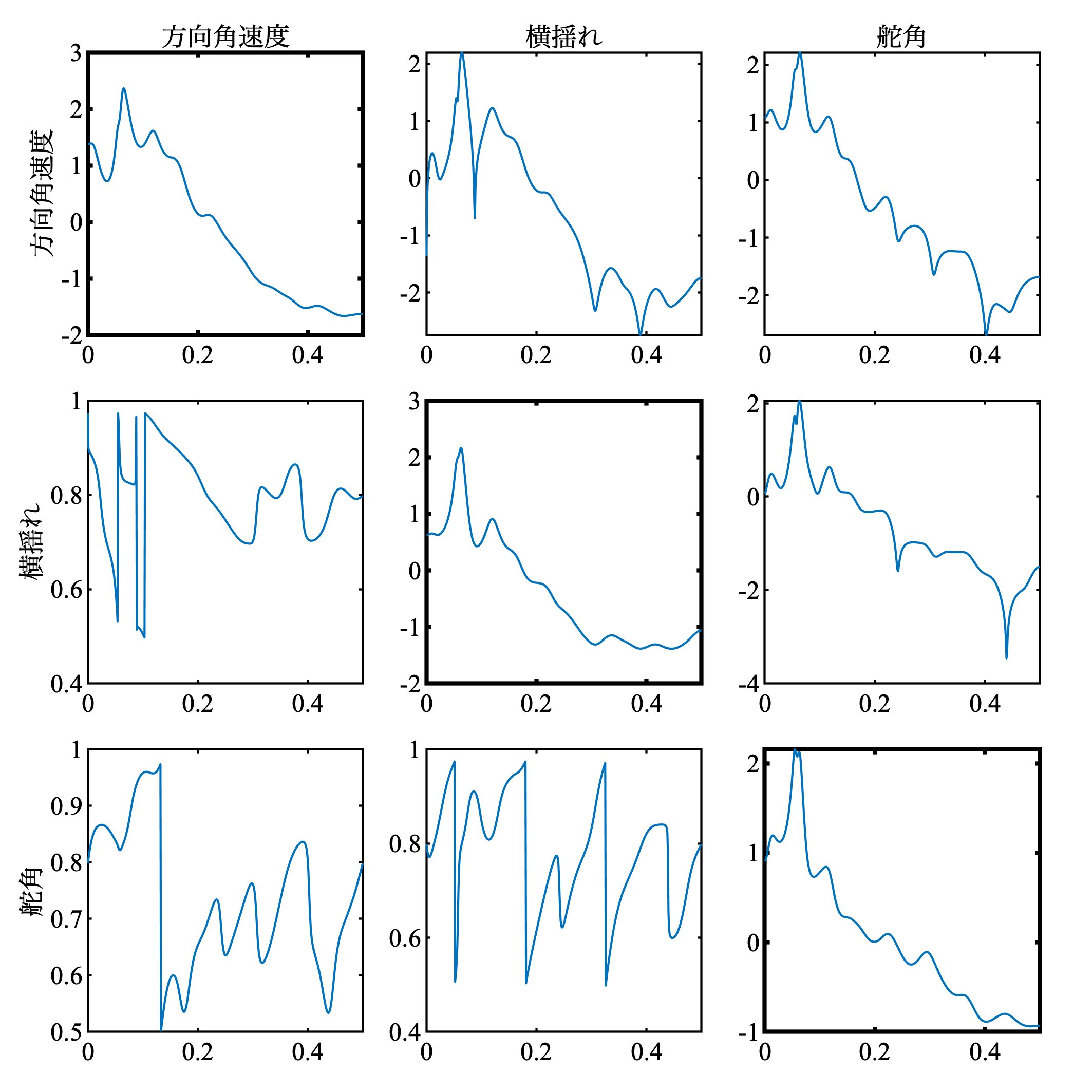
教科書図6.8に対応するものを作ったが, 結構差がある. なお, 選択されたAR次数は16であった. 教科書では何が選択されているのかは書かれておらずわからない.
MATLABコード
MATLAB
d = hakusan.velocity;
d = [d hakusan.yoko];
d = [d hakusan.dakaku];
% calculate AR coeff and AIC for AR(1) to AR(32)
K = 3;
lag = 32;
[aic, V, Arcoef, maic] = mvArNormaleq(d, K, lag);
bar(1:lag , aic - min(aic), 0.5, 'LineStyle', 'none');
% calculate cross spectrum
M = maic;
order = ['order' num2str(M)];
a = Arcoef.(order);
W = squeeze(V(:, :, M));
[spec, amp, phase, coh, power, rpower, f] = crossSpectrum(a, W);
% Plot
t = tiledlayout(3, 3); t.Padding = 'compact'; t.TileSpacing = 'compact';
ax = nexttile;
plot(f, log10(real(spec(:, 1, 1))))
xlim([0 0.5]); ax.LineWidth = 1; title('方向角速度'); ylabel('方向角速度')
ax = nexttile;
plot(f, log10(real(amp(:, 1, 2))))
xlim([0 0.5]); title('横揺れ');
ax = nexttile;
plot(f, log10(real(amp(:, 1, 3))))
xlim([0 0.5]); title('舵角');
ax = nexttile;
plot(f, log10(real(phase(:, 1, 2))))
xlim([0 0.5]); ylabel('横揺れ')
ax = nexttile;
plot(f, log10(real(spec(:, 2, 2))))
xlim([0 0.5]); ax.LineWidth = 1;
ax = nexttile;
plot(f, log10(real(amp(:, 2, 3))))
xlim([0 0.5]);
ax = nexttile;
plot(f, log10(real(phase(:, 1, 3))))
xlim([0 0.5]); ylabel('舵角')
ax = nexttile;
plot(f, log10(real(phase(:, 2, 3))))
xlim([0 0.5]);
ax = nexttile;
plot(f, log10(real(spec(:, 3, 3 ))))
xlim([0 0.5]); ax.LineWidth = 1;
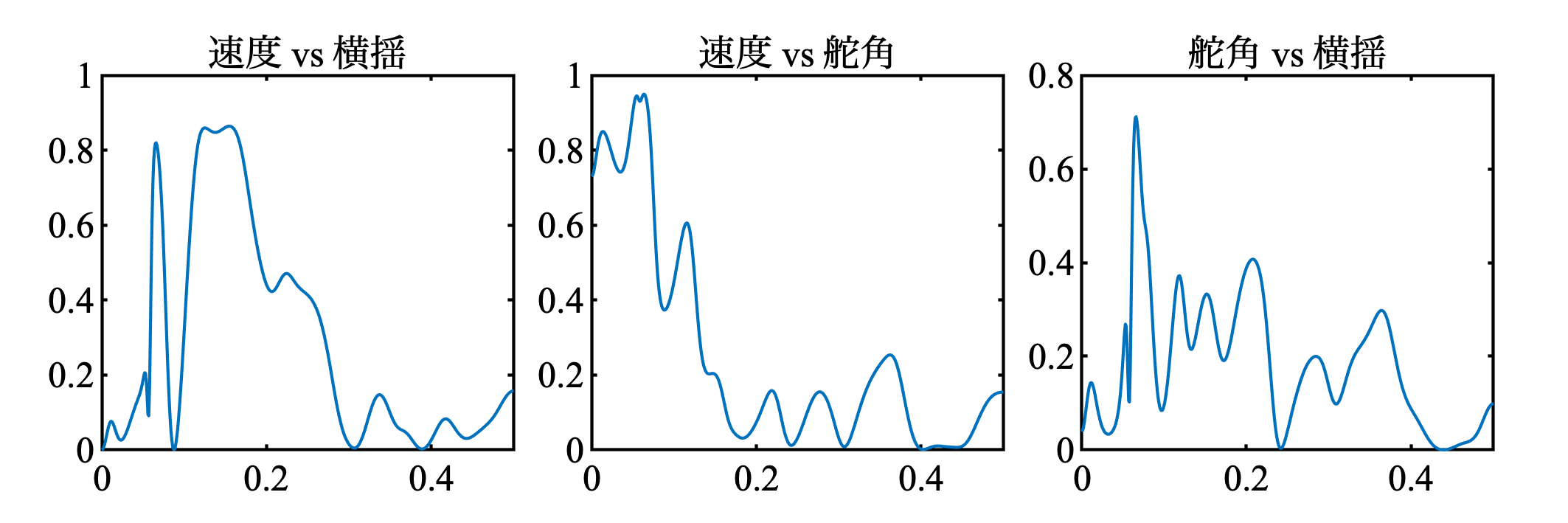
続いて, コヒーレンシー.
MATLABコード
MATLAB
t = tiledlayout(1, 3); t.Padding = 'compact'; t.TileSpacing = 'compact';
ax = nexttile;
plot(f, coh(:, 1, 2))
xlim([0 0.5]); title('速度 vs 横揺');
ax = nexttile;
plot(f, coh(:, 1, 3))
xlim([0 0.5]); title('速度 vs 舵角');
ax = nexttile;
plot(f, coh(:, 2, 3))
xlim([0 0.5]); title('舵角 vs 横揺');
そして, 相対パワー寄与率.
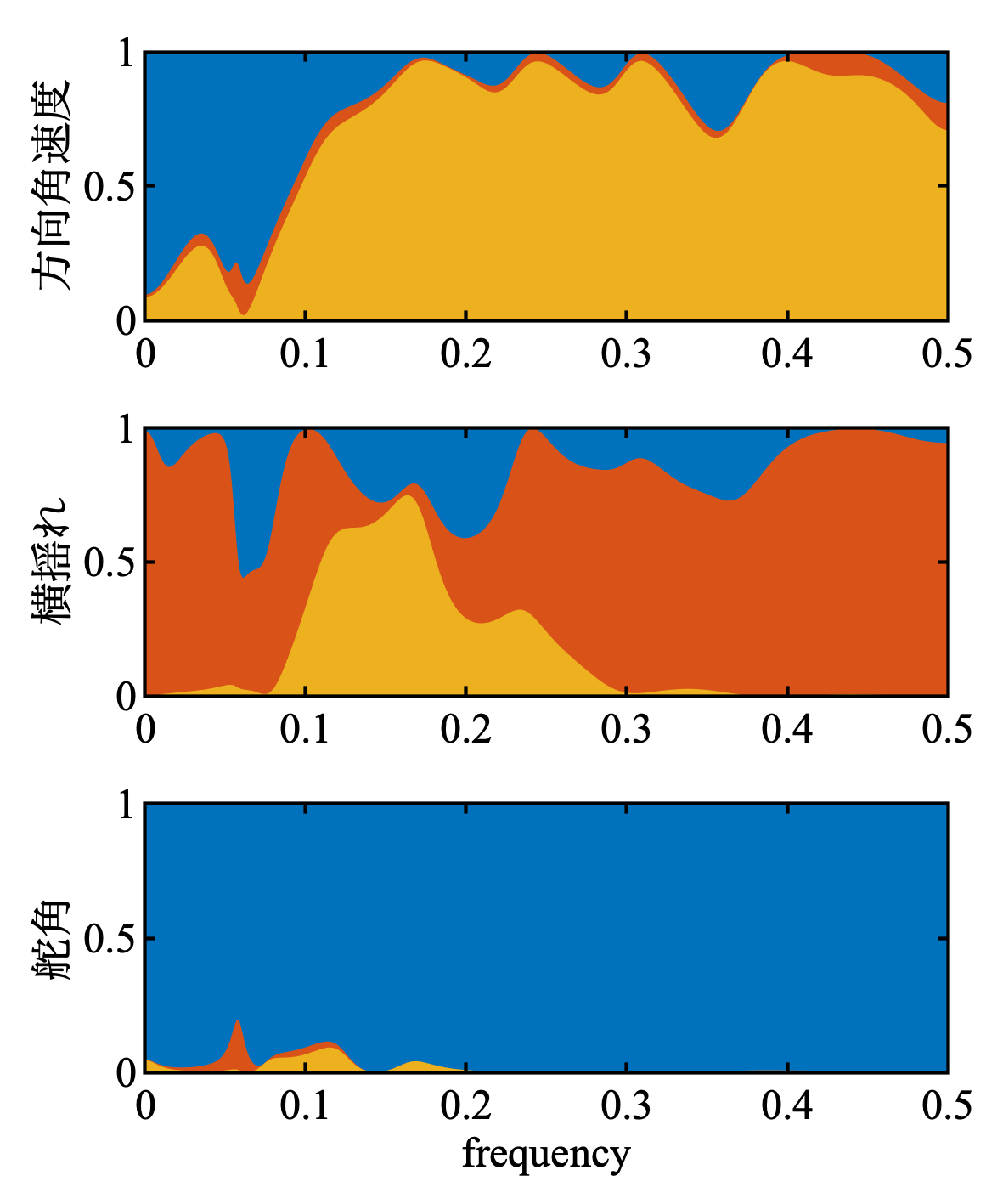
MATLABコード
MATLAB
t = tiledlayout(3, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';
titles = {'方向角速度', '横揺れ', '舵角'};
for target = 1:K
nexttile
for k = K:-1:1
area(f, rpower(:, target, k), 'LineStyle', 'none'); hold on
end
xlim([0 0.5]);
ylabel(titles{target})
end
xlabel('frequency')