MATLABで『時系列解析入門』7章
最終更新:2021/08/02
ARモデルの推定.
ここまででは, ある係数や次数をもつARモデルの性質 ( どのようなスペクトルをもつか, など ) について考察してきた. この章では, 実際のデータをARモデルとして扱う時, どのように係数や次数を推定するのかについて述べられている.
非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.
ARモデル
モデル
この章では, 時系列 $\{ y_n \}_{n=1}^N$ に対して以下で示される自己回帰モデルを当てはめる問題について考える.
尤度
ARモデルに従う時系列 $\{ y_n \}_{n=1}^N = \bm{y}$ の同時分布はN次元正規分布となり, 尤度は以下でかける.
$\mathcal{L}(\theta)$ を最大化する $\hat{\theta}$ がみつかれば, AICも以下となる.
では, どのように $\hat{\theta}$ を算出するか. 教科書では
- Levinsonのアルゴリズム
- 最小二乗法
- PARCOR法
Yule-Walker法
Yule-Walker推定量
第六章 で紹介した Yule-Walker方程式に, 標本自己共分散函数 $\hat{C}_k$ を代入した以下の式
Levinsonのアルゴリズム
では, 上のYule-Walker方程式をどう解いて, $m$ 次のYule-Walker推定量を求めようか. 第六章で作ったプログラムでコツコツ計算してもできるであろうが, Levinsonのアルゴリズムを使えばこれを効率的に解ける. 証明は教科書を見てほしい.
function [aic, Arcoef, s2, maic] = arLevinson(d, M)
%ARLEVINSON
%
% INPUT
% d:data
% M:maximum AR degree (lag)
%
% OUTPUT
% aic : AIC
% Arcoef : AR coefficient (structure)
% s2 : sigma^2
% maic : The order which provides the minimum AIC
% 前処理
d = d - mean(d);
N = length(d);
% 標本自己共分散を求める
C = xcorr(d, M)/N;
C = C(M+1:end);
% preallocation
aic = zeros(1, M+1);
s2 = zeros(1, M+1);
a = zeros(M);
% AIC_0
s2(1) = C(1);
aic(1) = N * (log(2 * pi * s2(1))+1) + 2;
% m = 1に対してアルゴリズムを回す
m = 1;
a(m, m) = C(m+1) / s2(1);
s2(2) = s2(1) * (1 - a(m, m)^2);
aic(m+1) = N * (log(2 * pi * s2(2)) + 1) + 2*(m + 1);
% m = 2, ... , Mに対してアルゴリズムを回す
for m = 2:M
% calculate a_m^m
a(m, m) = (C(m+1) - dot(a(m-1, 1:m-1), C(m:-1:2))) / s2(m);
% calculate a_i^m
for i = 1:m-1
a(m, i) = a(m-1, i) - a(m, m)*a(m-1, m-i);
end
% calculate sigma_{m-1}^2
s2(m+1) = s2(m) * (1 - a(m, m)^2);
% calculate AIC_m
aic(m+1) = N * (log(2 * pi * s2(m+1)) + 1) + 2*(m + 1);
end
% make Arcoef
for m = 1:M
name = ['order' num2str(m)];
Arcoef.(name) = a(m, 1:m);
end
% calculate maic
[~, maic] = min(aic);
end
最小二乗法
最小二乗法は, 多変量ARモデルの解析をする際に柔軟性が高いらしいので, ここに紹介する. データ$\vecseq{y}{1}{N}$ に対する, $M$ 次のARモデルの最小二乗階を求める手順だけ示す. とてもシンプル. MATLABのコードは, 可能な限り手順と一致するように書いている.
まず. 以下の行列 $X$ を作る.
qrを使える ) によって,
あとは, $j$ 次の自己回帰モデルの残差分散 $\hat{\sigma}^2$, AIC, 自己回帰係数は以下の式を解くことで得られる.
A\b を使えば, 後退代入できるときは後退代入してくれるので便利.
function [aic, Arcoef, s2, maic] = arLeastsquares(d, M)
%ARLEASTSQUARES
%
% INPUT
% d:data
% M:maximum AR degree (lag)
%
% OUTPUT
% aic : AIC
% Arcoef : AR coefficient (structure)
% s2 : sigma^2
% maic : The order which provides the minimum AIC
% preprocessing
d = d - mean(d);
N = length(d);
% make matrix X Eq.(7.19)
Z = zeros(N-M, M);
for I = 1:M
Z(:, I) = d(M-I+1:N-I);
end
y = d(M+1:N);
X = [Z y'];
% Householder(QR decomposition)
[~, R] = qr(X);
S = R(1:M+1, 1:M+1);
% calculate sigma^2, AIC
s2 = flipud(cumsum(flipud(S(:, end).^2)));
s2 = s2/(N-M);
aic = (N-M) * (log(2*pi*s2)+1) + 2*((0:M)' + 1);
% make Arcoef
for m = 1:M
name = ['order' num2str(m)];
res = S(1:m, 1:m)\S(1:m, M+1);
Arcoef.(name) = res';
end
% calculate maic
[~, maic] = min(aic);
maic = maic-1;
end
多変量ARモデル
モデル
多変量ARモデルでは, 時系列 $\bm{y}_n$ は以下の関係を想定する. ここで, データは $k$ 次元, ARモデルは $m$ 次とする.
Yule-Walker法
function [aic, V, Arcoef, maic] = mvArLevinson(d, K, M)
%MVARLEVINSON
%
% INPUT
% d:data
% k:dimension of the data
% M:maximum AR degree (lag)
%
% OUTPUT
% aic : AIC (size = lag * k)
% Arcoef : AR coefficient, size = K * K * M * M
% V : variance-covariance matrix
% maic : The order which provides the minimum AIC
% preprocessing
d = reshape(d, [], K);
d = d - mean(d);
N = size(d, 1);
% calculate C
C = xcorr(d, M)/N;
C = C(M+1:end, :);
C = reshape(C, M+1, K, K);
C = permute(C,[3 2 1]);
C0 = C(:, :, 1);
C = C(:, :, 2:end);
% preallocation
aic = zeros(1, M);
V = zeros(K, K, M); % = zeros(size(C))
U = zeros(K, K, M);
A = zeros(K, K, M, M);
B = zeros(K, K, M, M);
% Yule Walker
% m = 0
V0 = C0;
U0 = C0;
aic0 = N * (K*log(2*pi) + log(det(V0)) + K) + K*(K+1);
% m = 1 (W_1 = C_1)
A(:, :, 1, 1) = C(:, :, 1) / U0;
B(:, :, 1, 1) = C(:, :, 1)'/ V0;
V(:, :, 1) = C0 - A(:, :, 1, 1) * C(:, :, 1)';
U(:, :, 1) = C0 - B(:, :, 1, 1) * C(:, :, 1);
aic(1) = N * (K*log(2*pi) + log(det(V(:, :, 1))) + K) + K*(K+1) + 2*K^2*1;
% m = 2 ,..., M
for m = 2:M
W = C(:, :, m) - sum(pagemtimes(squeeze(A(:, :, m-1, 1:m-1)), C(:, :, m-1:-1:1)), 3);
A(:, :, m, m) = W /U(:, :, m-1);
B(:, :, m, m) = W'/V(:, :, m-1);
for i = 1:m-1
A(:, :, m, i) = A(:, :, m-1, i) - A(:, :, m, m) * B(:, :, m-1, m-i);
B(:, :, m, i) = B(:, :, m-1, i) - B(:, :, m, m) * A(:, :, m-1, m-i);
end
tC = permute(C, [2 1 3]);
V(:, :, m) = C0 - sum(pagemtimes(squeeze(A(:, :, m, 1:m)), tC(:, :, 1:m)), 3);
U(:, :, m) = C0 - sum(pagemtimes(squeeze(B(:, :, m, 1:m)), C(:, :, 1:m)), 3);
aic(m) = N * (K*log(2*pi) + log(det(V(:, :, m))) + K) + K*(K+1) + 2*K^2*m;
end
% make Arcoef
for m = 1:M
name = ['order' num2str(m)];
Arcoef.(name) = squeeze(A(:, :, m, 1:m));
end
% calculate maic
aic = [aic0 aic];
[~, maic] = min(aic);
maic = maic-1;
end
例として, 船舶データ ( HAKUSAN ) に適用してみた. 4変数, 最大次数60でトライ. 正直複雑でコードに自信がないけど, 最小AICを与える次数は10で, 教科書とおなじになった. AICの増加の仕方も直線的でいい感じ.
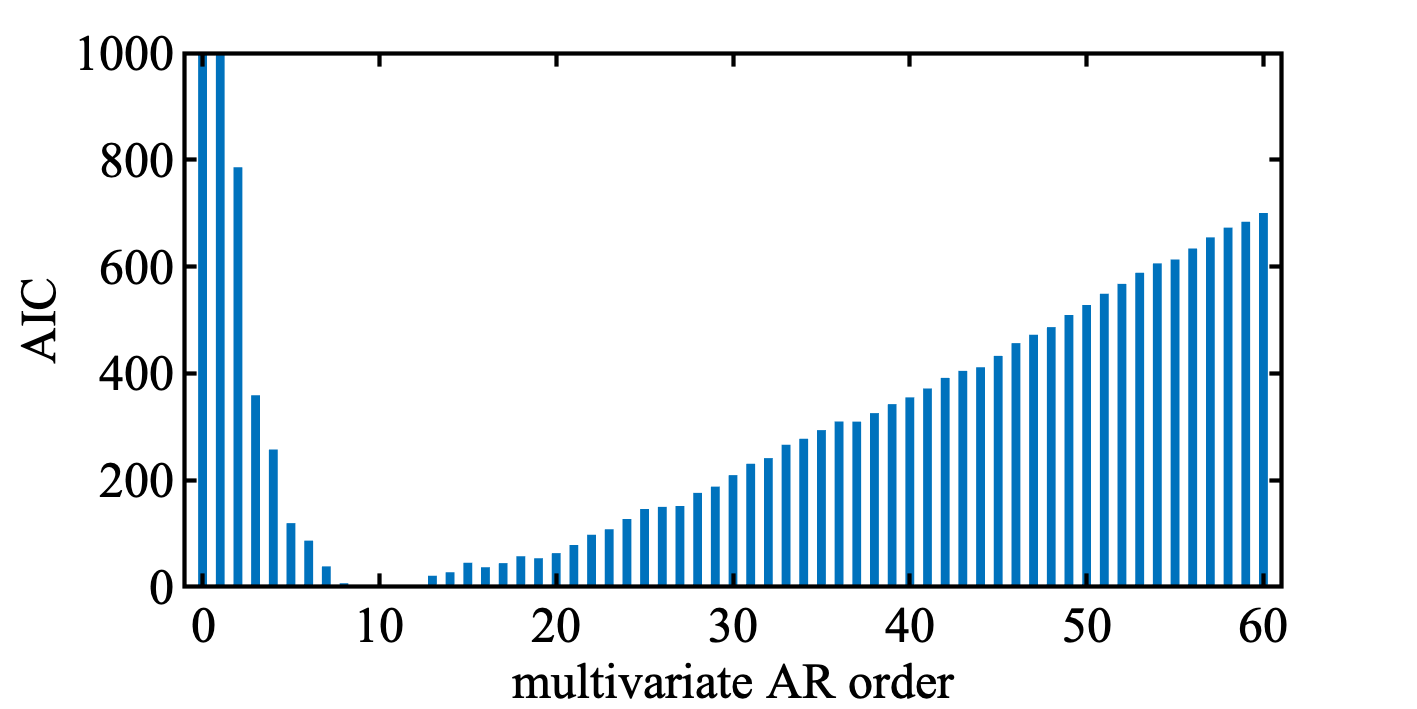
MATLABコード
MATLAB
d = hakusan.velocity;
d = [d hakusan.yoko];
d = [d hakusan.tate];
d = [d hakusan.dakaku];
K = 4;
M = 60;
[aic, V, Arcoef, maic] = mvArLevinson(d, K, M);
bar(0:M, aic - min(aic), 0.5, 'LineStyle', 'none');
ylim([0 1000])
ylabel('AIC')
xlabel('multivariate AR order')
数値例: ( 単変量 ) ARモデル
太陽黒点数 ( Yule-Walker法 )
SUNSPOTデータを対数変換 ( 底は10, 0には $10^{0.1}$ を代入 ) し, Yule-Walker法を用いて, 次数20までのARモデルを推定し, AICを計算した.
AICは最小値を0にシフトして表示している.
教科書通り次数10のARモデルが選択されている ( maicは10 ) .
残差分散は単調に減少している.
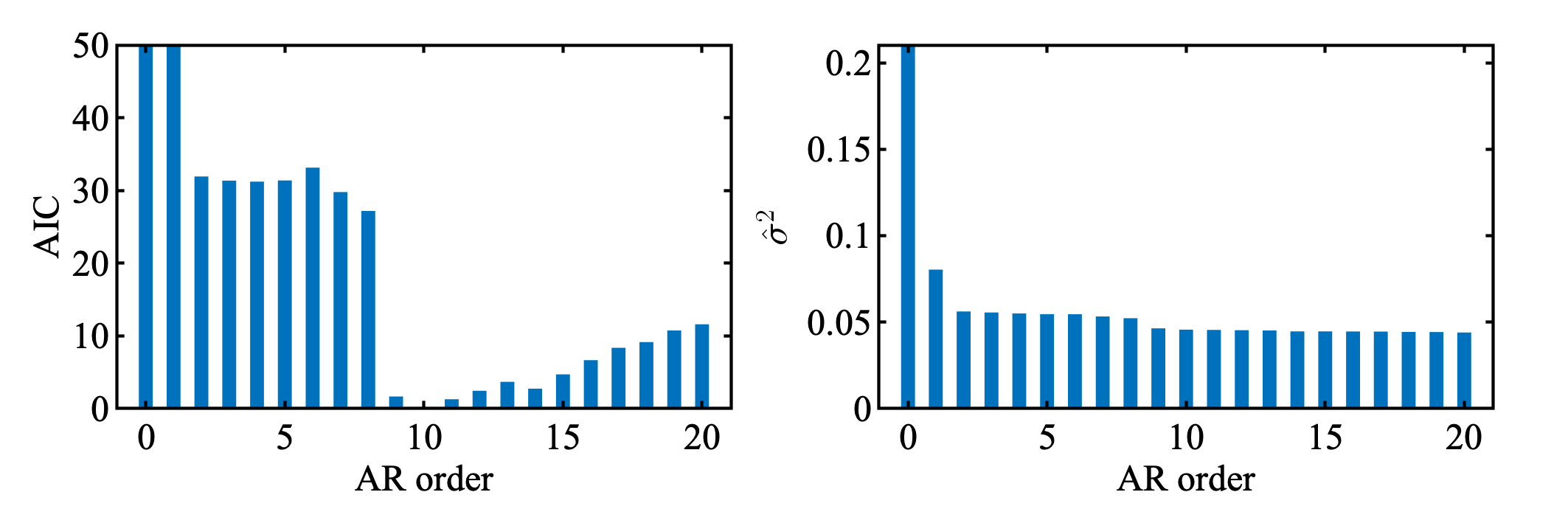
MATLABコード
MATLAB
d = sunspot; % data
d(d==0) = 10^0.1;
d = log10(d);
M = 20; % 最大AR次数
[aic, Arcoef, s2, maic] = arLevinson(d, M);
t = tiledlayout(1, 2); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
bar(0:20, aic-min(aic), 0.5, 'LineStyle', 'none')
ylim([0 50]);
xlabel('AR order')
ylabel('AIC')
nexttile
bar(0:20, s2, 0.5, 'LineStyle', 'none')
% ylim([0 50]);
xlabel('AR order')
ylabel('$\hat{\sigma}^2$','Interpreter','latex')
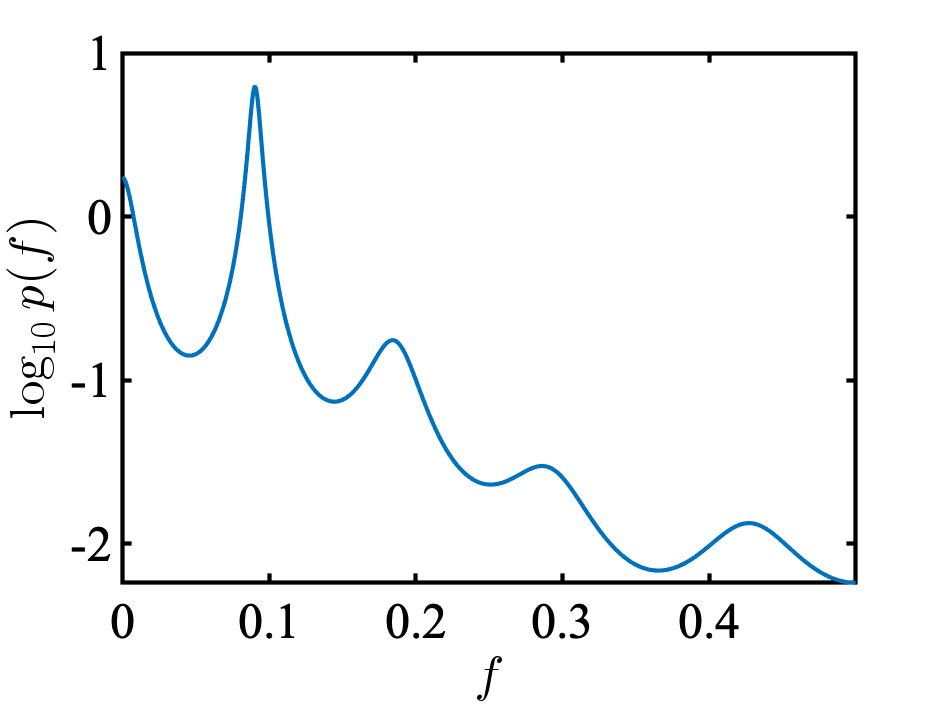
次に, AR(10)のパワースペクトルをみてみる. 教科書とほとんどおなじになった. ピークは, 0.09 [cycle/year] にあり, 1/0.09 = 約11で, 約11年周期の黒点数の変動が表現されている.
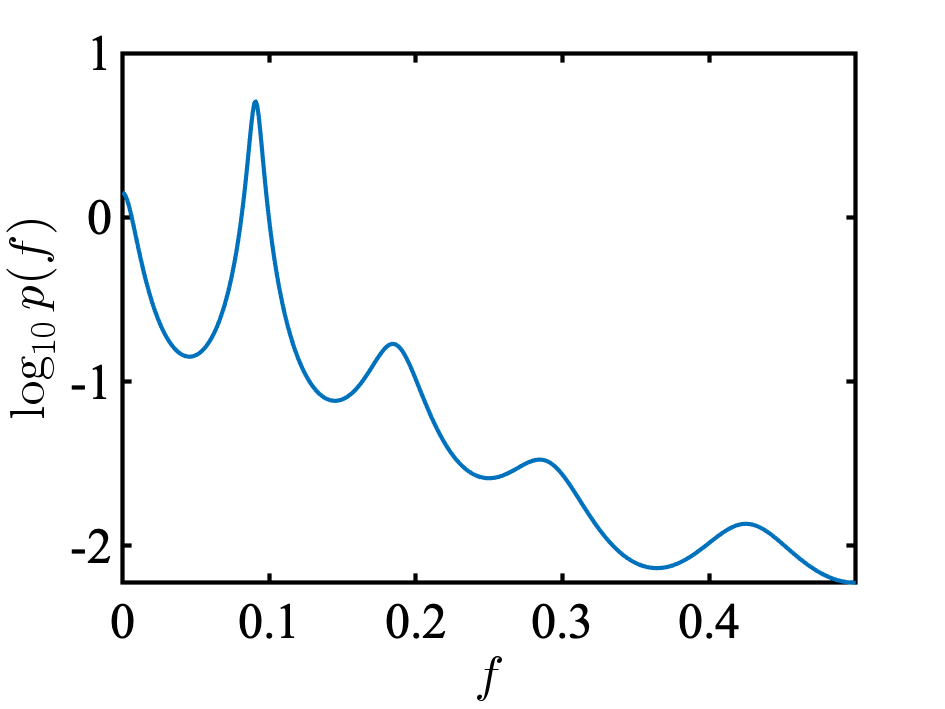
太陽黒点数 ( 最小二乗法 )
念の為, 最小二乗法も使ってみる.
同じ結果であろう.
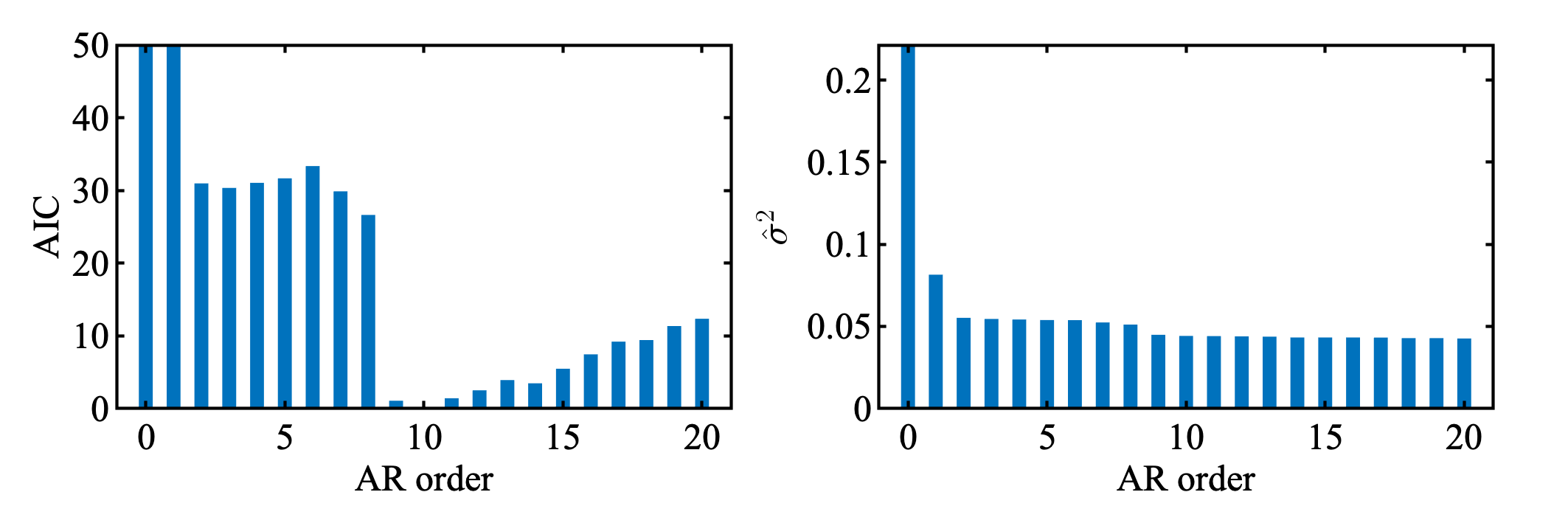
MATLABコード
MATLAB
d = sunspot; % data
d(d==0) = 10^0.1;
d = log10(d);
M = 20; % 最大AR次数
[aic, Arcoef, s2, maic] = arLeastsquares(d, M);
t = tiledlayout(1, 2); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
bar(0:M, aic-min(aic), 0.5, 'LineStyle', 'none')
ylim([0 50]);
xlabel('AR order')
ylabel('AIC')
nexttile
bar(0:M, s2, 0.5, 'LineStyle', 'none')
xlabel('AR order')
ylabel('$\hat{\sigma}^2$','Interpreter','latex')
%% - Spectrum
lag = 10;
order = ['order' num2str(lag)];
[~, ~] = spectrumARMA(Arcoef.(order), 0, s2(lag+1), true);
シミュレーション
せっかくなので選ばれたAR(10)モデルから発生する時系列をシミュレーションしてみた. 内容的には. 教科書16.3節「ARMAモデルのシミュレーション」である.
もちろん, 乱数によって発生するデータの雰囲気はかわる. よさげ ( つまり, 太陽黒点数の原データと雰囲気が似ている ) ものと, 微妙なものを以下に載せる.
Good
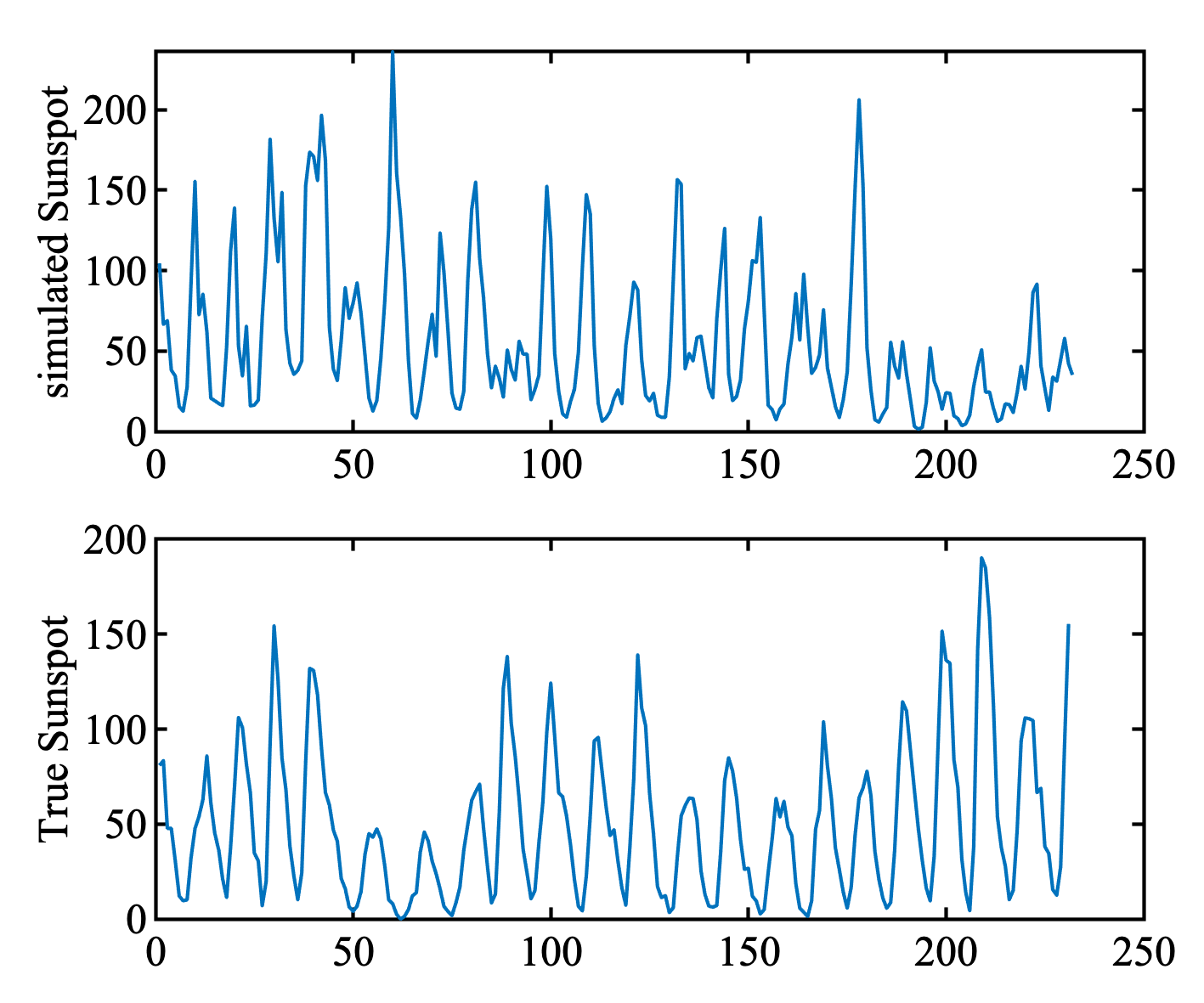
Bad
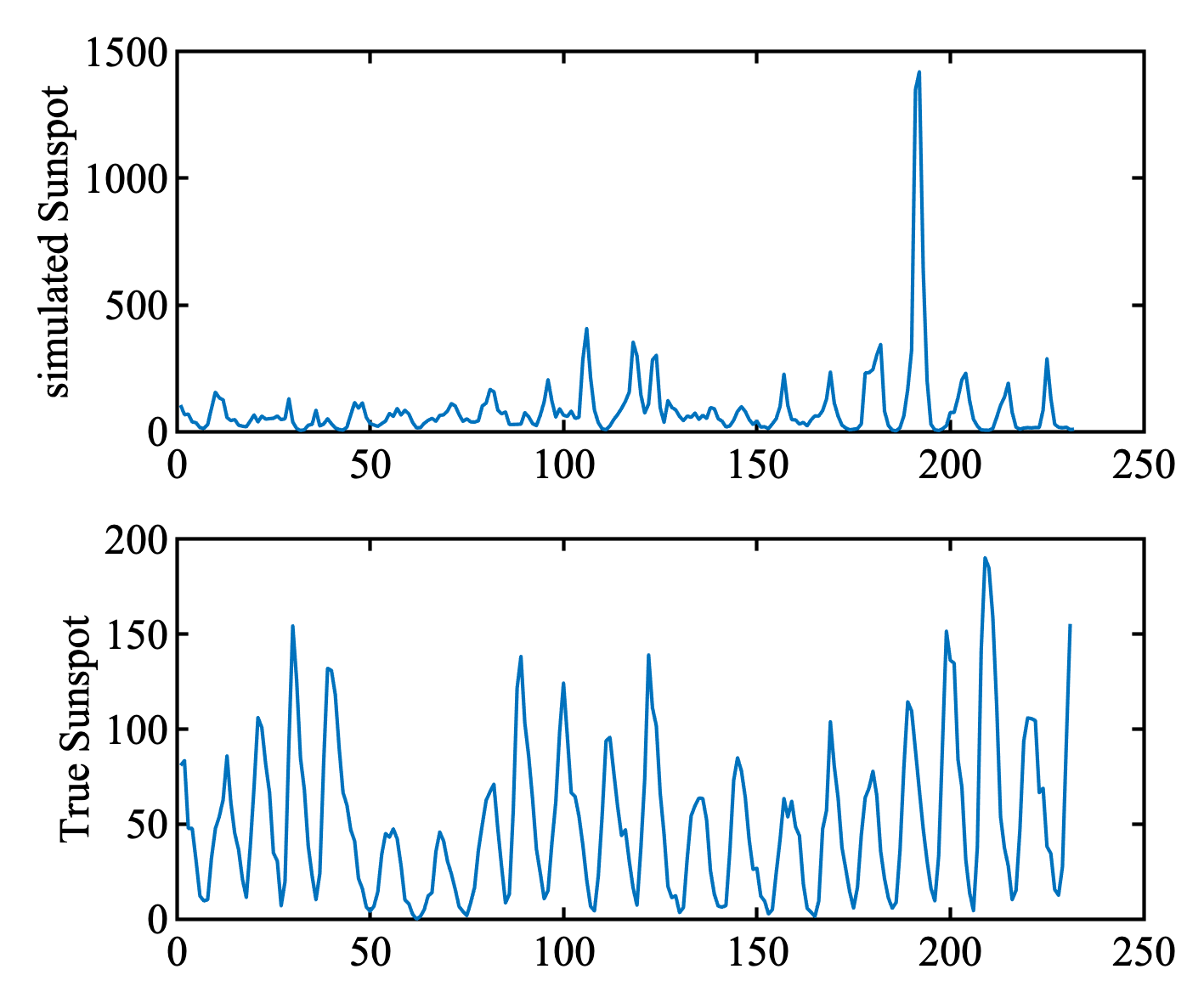
MATLABコード
MATLAB
lag = 10; % AR次数
stdev = sqrt(s2(lag+1)); % 残差の標準偏差
order = ['order' num2str(lag)];
arcoef = Arcoef.(order); % AR係数
rng('shuffle')
L = 231; % シミュレーションする時系列の長さ ( 原データに合わせた ) .
ySim = zeros(L, 1);
ySim(1:lag) = d(end-lag+1:end) - mean(d);
for I = lag:L
ySim(I+1) = dot(arcoef, ySim(I:-1:I-lag+1)) + randn * stdev;
end
% plot
y = sunspot;
t = tiledlayout(2, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
plot(10.^(ySim + mean(d)))
ylabel('simulated Sunspot')
nexttile
plot(y)
ylabel('True Sunspot')
書かなかった内容
今回, うまく再現できなかったなどの理由で書かなかった内容は, 以下.
- 最小二乗法による多変量ARモデル推定
- クロススペクトル・コヒーレンシー
- パワースペクトル分解・相対パワー寄与率
主な参考文献
今回から, 新装版に変えた. Rによる 時系列モデリング入門