MATLABで『時系列解析入門』６章

最終更新：2021/07/27

６章：ARMAモデルによる時系列の解析


非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

ARMAモデルの定義

時系列 $y_n$ を以下で表現するモデル.

\begin{align}\large{ y_n = \sum_{i=1}^{m}a_i y_{n-i} + v_n + \sum_{i=1}^{\ell}b_i v_{n-i} \notag }\end{align}
ここで,
  • $m$：自己回帰の次数
  • $a_i$：自己回帰係数
  • $\ell$：移動平均の次数
  • $b_i$：移動平均係数

また, $v_n$ は白色雑音, つまり以下を満たす ( $\mathbb{E}[\cdot]$ は期待値 ) .
  • $\mathbb{E}[v_n] = 0$
  • $\mathbb{E}[v_n^2] = \sigma^2$
  • $\mathbb{E}[v_n v_m] = 0 \; (m \neq n)$
  • $\mathbb{E}[v_n y_m] = 0 \; (m \lt n)$

ARMAモデルの性質や表現

インパルス応答函数

ARMAモデルに従う時系列 $y_n$ が, 以下のように, 無限次の移動平均モデルで表されるというのは不思議で面白いなと思う.

\begin{align}\large{ y_n = \sum_{i=0}^{\infty} g_i v_{n-i}, \notag }\end{align}
$g_i$ はインパルス応答函数とよばれ, 以下で計算できる.
\begin{align}\large{ g_0 = 1, \tag{6.8} \\ g_i = \sum_{j = 1}^{i} a_j g_{i-j} - b_i. }\end{align}

下のMATLAB函数は, K期後までのインパルス応答函数を求める函数である. ここで, $\sum_{j = 1}^{i} a_j g_{i-j}$ の部分は内積で計算している. 例えば, $i = 5$ のとき, この和は, $a_1g_4 + a_2g_3 + a_3g_2 + a_4g_1 + a_5g_0$ なので,

\begin{align} (a_1, a_2, a_3, a_4, a_5)\cdot(g_4, g_3, g_2, g_1, g_0) \notag \end{align}
と計算した.

MATLAB 
function [g, k] =impulseResARMA(a, b, K)

k = 0:K;

a = reshape(a, 1, []);
a = [a zeros(1, K+1-length(a))]; % ゼロでパディング

b = reshape(b, 1, []);
b = [b zeros(1, K+1-length(b))]; % ゼロでパディング

g = zeros(size(k));
g(1) = 1;

for I = 1:K
    
   g(I+1) = dot(a(1:I), g(I:-1:1)) - b(I); 
end

end

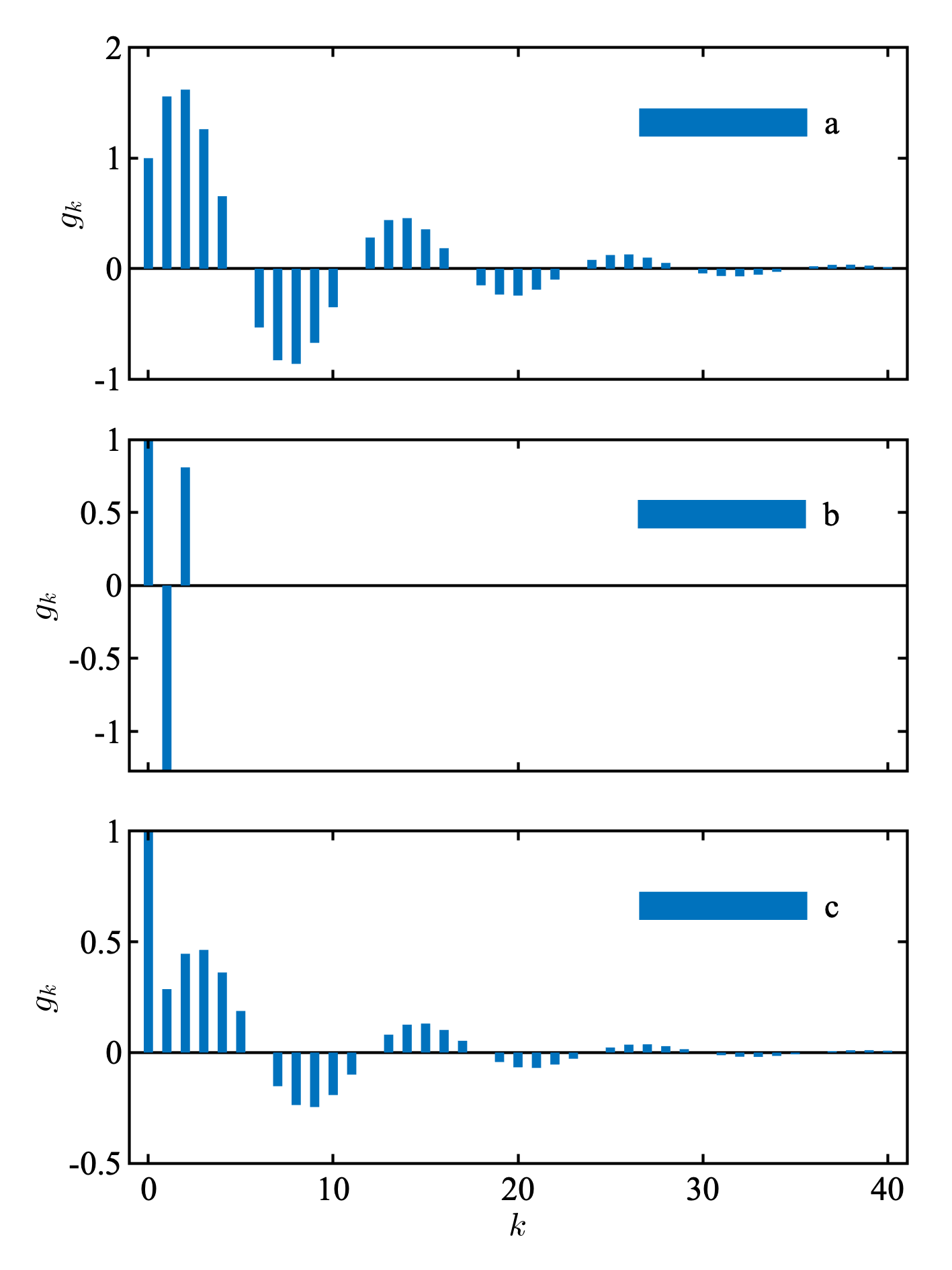
これを用いて, 教科書の例を計算してみる.

  1. $y_n = 0.9 \sqrt{3} y_{n-1} - 0.81 y_{n-2} + v_n$ (2次のARモデル)
  2. $y_n = v_n - 0.9 \sqrt{2} v_{n-1} + 0.81 v_{n-2}$ (2次のMAモデル)
  3. $y_n = 0.9 \sqrt{3} y_{n-1} - 0.81 y_{n-2} + v_n - 0.9 \sqrt{2} v_{n-1} + 0.81 v_{n-2}$
    ((2, 2)次のMAモデル)

name
MATLABコード MATLAB 
K = 40; % 教科書の倍に設定してみた

a = [0.9*sqrt(3) -0.81];
b = [0.9*sqrt(2) -0.81];

t = tiledlayout(3, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';

nexttile
[g, k] = impulseResARMA(a, 0, K);
bar(k, g, 0.5, 'LineStyle', 'none');
xticklabels({})
ylabel('$g_k$','Interpreter','latex')
legend('a', 'Box', 'off')

nexttile
[g, k] = impulseResARMA(0, b, K);
bar(k, g, 0.5, 'LineStyle', 'none');
xticklabels({})
ylabel('$g_k$','Interpreter','latex')
legend('b', 'Box', 'off')

nexttile
[g, k] = impulseResARMA(a, b, K);
bar(k, g, 0.5, 'LineStyle', 'none');
xlabel('$k$','Interpreter','latex')
ylabel('$g_k$','Interpreter','latex')
legend('c', 'Box', 'off')

自己共分散函数

ARMAモデルの自己共分散函数 $C_k$ は以下の方程式(6.11)で求まる. 寄与とするのは, $m$, $\ell$, $a_i$, $b_i$, $\sigma^2$ である.

\begin{align}\large{ C_0 = \sum_{i=1}^{m} a_i C_i + \sigma^2 \left\{ 1 - \sum_{i=1}^{\ell} b_i g_i \right\}, \tag{6.11} \\ C_k = \sum_{i=1}^{m} a_i C_{k-i} - \sigma^2 \sum_{i=1}^{\ell} b_i g_{i-k}. \label{yw} }\end{align}
なお, $\ell = 0$, つまり, ARモデルの場合, 以下のYule-Walker方程式となる.
\begin{align}\large{ C_0 = \sum_{i=1}^{m} a_i C_i + \sigma^2, \tag{Yule-Walker Eq.} \\ C_k = \sum_{i=1}^{m} a_i C_{k-i}. }\end{align}

以下にMATLABで実装する. 以下の2点に注意.

  • $C_k = C_{-k}$
  • $g_k = 0 \; (k \lt 0)$

コードの内容が少し複雑なので, どのように計算したのか以下に示す. もっといいやり方があると思う. . .

コードの解説 ( click )

式 \eqref{yw} を以下のように書き直す.

\begin{align} C_0 & = \sum_{i=1}^{m} a_i C_i + b_0 \\ C_k & = \sum_{i=1}^{m} a_i C_{k-i} + b_i. \end{align}
これをとけばいいわけだが, わかりやすいように $m = 4$, $C_{40}$ まで求めるとして, 書き下してみる.
\begin{align} C_0 & = a_1 C_1 + a_2 C_2 + a_3 C_3 + a_4 C_4 + b_0, \\ C_1 & = a_1 C_0 + a_2 C_1 + a_3 C_2 + a_4 C_3 + b_1, \notag \\ C_2 & = a_1 C_1 + a_2 C_0 + a_3 C_1 + a_4 C_2 + b_2, \notag \\ C_3 & = a_1 C_2 + a_2 C_1 + a_3 C_0 + a_4 C_1 + b_3, \notag \\ C_4 & = a_1 C_3 + a_2 C_2 + a_3 C_1 + a_4 C_0 + b_4, \notag \\ C_5 & = a_1 C_4 + a_2 C_3 + a_3 C_2 + a_4 C_1 + b_5, \notag \\ \vdots \notag \\ C_{40} & = a_1 C_{39} + a_2 C_{38} + a_3 C_{37} + a_4 C_{36} + b_{40}. \notag \end{align}
この連立方程式を解けばいい. 行列で書くと,
\begin{align} \begin{pmatrix} C_0 \\ C_1 \\ C_2 \\ C_3 \\ C_4 \\ C_5 \\ \vdots \\ C_{40} \end{pmatrix} = \begin{pmatrix} 0 & a_1 & a_2 & a_3 & a_4 & 0 & \cdots & 0 & 0 & 0 \\ a_1 & a_2 & a_3 & a_4 & 0 & 0 & \cdots & 0 & 0 & 0 \\ a_2 & a_1 + a_3 & a_4 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 \\ a_3 & a_2 + a_4 & a_1 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 \\ a_4 & a_3 & a_2 & a_1 & 0 & 0 & \cdots & 0 & 0 & 0 \\ 0 & a_4 & a_3 & a_2 & a_1 & 0 & \cdots & 0 & 0 & 0 \\ & & & \vdots & & & & & & \\ 0 & 0 & 0 & 0 & 0 & 0 & \cdots & a_2 & a_1 & 0 \\ \end{pmatrix} \begin{pmatrix} C_0 \\ C_1 \\ C_2 \\ C_3 \\ C_4 \\ C_5 \\ \vdots \\ C_{40} \end{pmatrix} + \begin{pmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5 \\ \vdots \\ b_{40} \end{pmatrix}. \end{align}
記号でまとめて上の式を以下のように書くと,
\begin{align} \boldsymbol{c} = \mathbf{M}\boldsymbol{c} + \boldsymbol{b} \end{align}
となるので, 結局
\begin{align} (\mathbf{E} - \mathbf{M})\boldsymbol{c} = \boldsymbol{b} \tag{A} \end{align}
という線形方程式をとくことになる ( $\mathbf{E}$ は単位行列 ) .

では, $\mathbf{M}$ をどう作るかだが, 僕のコードでは以下のような行列を作り,

\begin{align} \begin{pmatrix} 0 & \cdots & \cdots & 0 & 0 & 0 & \color{red}{0} & a_1 & a_2 & a_3 & a_4 & 0 & \cdots & \cdots \\ 0 & \cdots & \cdots & 0 & 0 & 0 & \color{red}{a_1} & a_2 & a_3 & a_4 & 0 & 0 & \cdots & \cdots \\ 0 & \cdots & \cdots & 0 & 0 & a_1 & \color{red}{a_2} & a_3 & a_4 & 0 & 0 & 0 & \cdots & \cdots \\ 0 & \cdots & \cdots & 0 & a_1 & a_2 & \color{red}{a_3} & a_4 & 0 & 0 & 0 & 0 & \cdots & \cdots \\ 0 & \cdots & \cdots & a_1 & a_2 & a_3 & \color{red}{a_4} & 0 & 0 & 0 & 0 & 0 & \cdots & \cdots \\ 0 & \cdots & \cdots & a_2 & a_3 & a_4 & \color{red}{0} & 0 & 0 & 0 & 0 & 0 & \cdots & \cdots \\ & & & & & & \color{red}{\vdots} & & & & & & & \\ & & & & & & \color{red}{\vdots} & & & & & & & \\ \end{pmatrix} \end{align}
赤色の列を軸に対称に折り返してたしあわせることで作成している.

$\ell \neq 0$ のとき, つまりYule-Walker方程式とならないときは, ベクトル $\boldsymbol{b}$ も作らなければいけない. コード内にある, Gやggは, $\boldsymbol{b}$ をつくる過程の変数である.


MATLAB 
function [C, k] = autocovARMA(a, b, s2, K)
%AUTOCOVARMA  
%
% INPUTS:
%   a : 自己回帰係数
%   b : 移動平均係数
%   s2: 雑音の分散
%   K : K期後まで求める

l = length(b) * sign(sum(b~=0));

% gを計算
[g, k] =impulseResARMA(a, b, K);

a = reshape(a, 1, []);
b = reshape(b, 1, []);
a = [a zeros(1, K-length(a))]; % ゼロでパディング

　  % 行列Mの作成
M = zeros(K+1, 2*K+1);
aa = [zeros(1, K+1) a];
for I = 1:K+1
    M(I, :) = circshift(aa, 1-I);
end
temp = M(:, 1:K);
temp = fliplr(temp);
M    = M(:, K+1:end);
M(:, 2:end) = M(:, 2:end) + temp;

% l = 0でないなら, ベクトルbを作成. 
if l ~= 0
    p0 = s2 * (1 - dot(b, g(2:l+1)));

    gg = [g(1:l) zeros(1, K-l+1)];

    G = zeros(K, K+1);
    for I = 1:K
        G(I, :) = circshift(gg, I-1); 
    end

    p = -s2 * b * G(:, 1:l)';
    p = [p0 p];
else % solve Yule-Walker equation
    p = [s2 zeros(1, K)]; 
end

M = eye(K+1) - M;

C = M\p'; % 式 ( A ) をとく. 
    
end

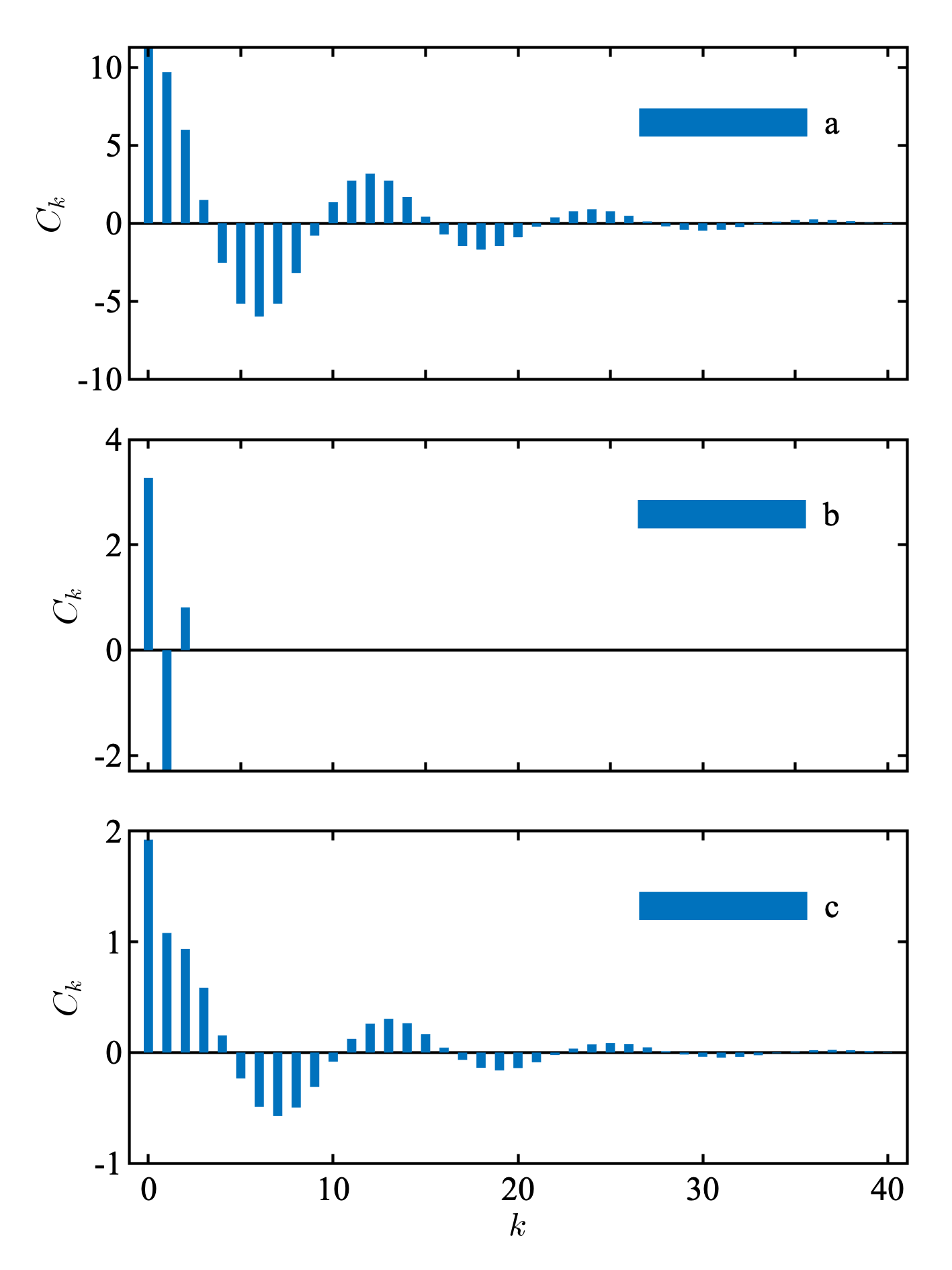
教科書の例を計算した. 教科書図6.2と一致している

name
MATLABコード MATLAB 
K = 40; % 教科書の倍に設定してみた
s2 = 1; % 教科書には明記されていなかったけれど, 分散1で計算したら教科書と一致した. 
a = [0.9*sqrt(3) -0.81];
b = [0.9*sqrt(2) -0.81];

t = tiledlayout(3, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';

nexttile
[C, k] = autocovARMA(a, 0, s2, 40);
bar(k, C, 0.5, 'LineStyle', 'none');
xticklabels({})
ylabel('$C_k$','Interpreter','latex')
legend('a', 'Box', 'off')

nexttile
[C, k] = autocovARMA(0, b, s2, 40);
bar(k, C, 0.5, 'LineStyle', 'none');
xticklabels({})
ylabel('$C_k$','Interpreter','latex')
legend('b', 'Box', 'off')

nexttile
[C, k] = autocovARMA(a, b, s2, 40);
bar(k, C, 0.5, 'LineStyle', 'none');
xlabel('$k$','Interpreter','latex')
ylabel('$C_k$','Interpreter','latex')
legend('c', 'Box', 'off')

ARMAモデルのパワースペクトル

次数 ($m$, $\ell$ ) のARMAモデルのパワースペクトルは, 次の式で求められる.

\begin{align}\large{ p(f) = \sigma^2 \frac {\left| 1- \sum_{j = 1}^{\ell} b_j \exp{(-2\pi\sqrt{-1}jf)} \right|^2} {\left| 1- \sum_{j = 1}^{m} a_j \exp{(-2\pi\sqrt{-1}jf)} \right|^2}. }\end{align}

コードは以下.

MATLAB 
function [p, f] = spectrumARMA(a, b, s2, doPlot, df)
% SPECTRUMARMA
% 
% a: AR coeff.
% b: MA coeff.
% s2:variance
% doPlot: if true, plot spectrum
% df: resolution(optional)
% 
% result can be seen with plot(f, log10(p))

a = reshape(a, [], 1);
b = reshape(b, [], 1);

if ~exist('df', 'var'),     df     = 0.001; end
if ~exist('doPlot', 'var'), doPlot = false; end

m = length(a);
l = length(b);

f = 0:df:0.5;
j = 1:m;
k = 1:l;

tmp = -2*pi*1i;

if isequal(a, 0)
    den = 1;
else
    den = abs(1 - exp(tmp*j.*f')*a).^2;
end

if isequal(b, 0)
    num = 1;
else
    num = abs(1 - exp(tmp*k.*f')*b).^2;
end

p = s2 * num ./ den;

if doPlot
    plot(f, log10(p));
    ylabel('$\log{p(f)}$','Interpreter','latex')
    xlabel('$f$','Interpreter','latex')
    xlim([0 0.5])
end
end

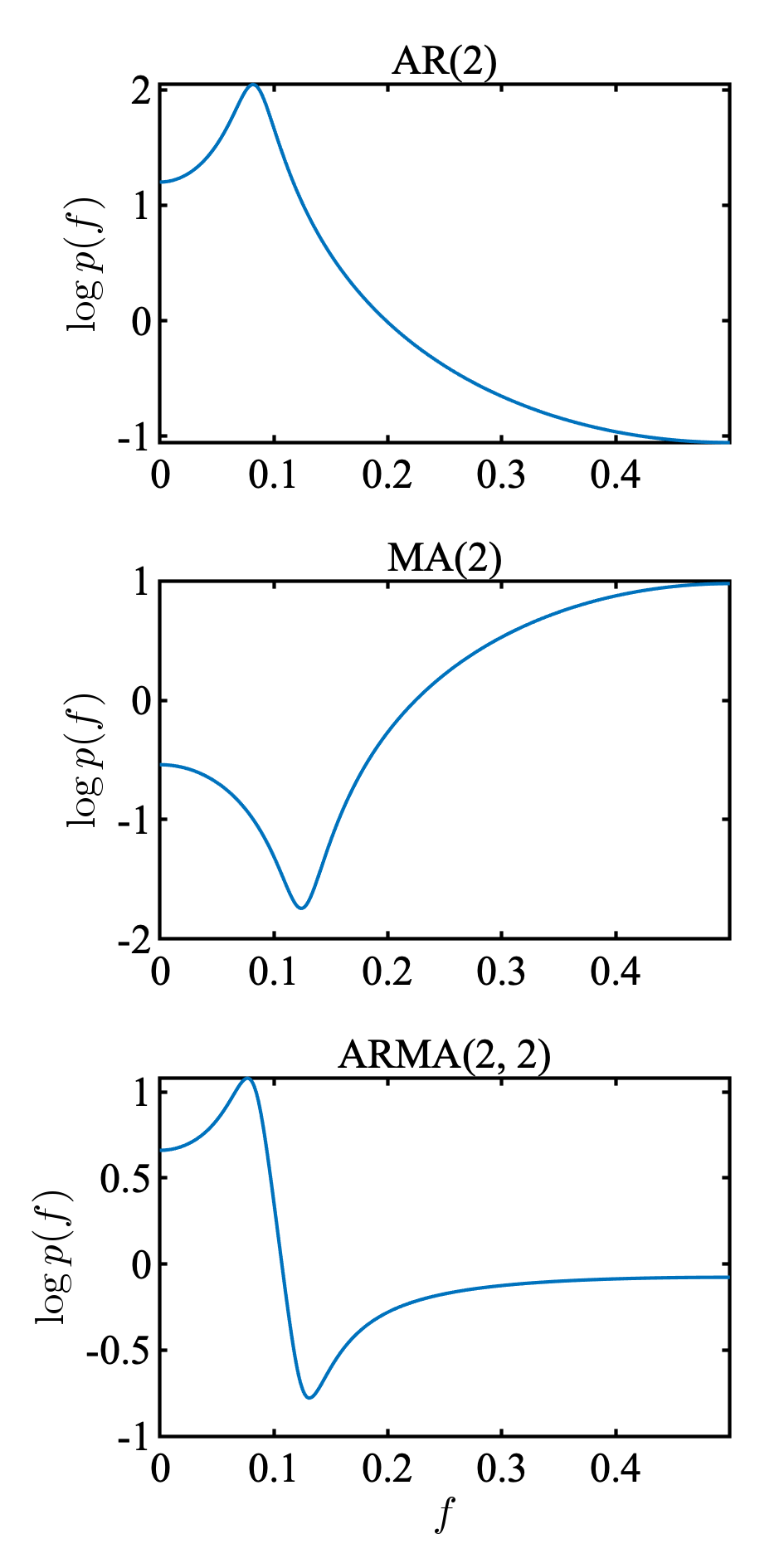
教科書の図6.4を再現してみる.

name
MATLABコード MATLAB 
a = [0.9*sqrt(3) -0.81];
b = [0.9*sqrt(2) -0.81];

t = tiledlayout(3, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
[p, f] = spectrumARMA(a, 0, 1);
plot(f, log10(p)); title('AR(2)')
ylabel('$\log{p(f)}$','Interpreter','latex')
xlim([0 0.5])

nexttile
[p, f] = spectrumARMA(0, b, 1);
plot(f, log10(p)); title('MA(2)')
ylabel('$\log{p(f)}$','Interpreter','latex')
xlim([0 0.5])

nexttile
[p, f] = spectrumARMA(a, b, 1);
plot(f, log10(p)); title('ARMA(2, 2)')
ylabel('$\log{p(f)}$','Interpreter','latex')
xlabel('$f$','Interpreter','latex')
xlim([0 0.5])

その他

これ以降の内容は, 実際のデータに対するAR次数の決定の問題などを含んでいるため, 後回しにする. $\rightarrow$ 第七章, 第七章の追記.

主な参考文献


この記事のTOP    BACK    TOP