MATLABで『時系列解析入門』４章

最終更新：2021/07/22


非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

最尤法によるコーシー分布のパラメータの推定

最尤法を用いて, コーシー分布に対するパラメータ推定を行う. データは, 以下の10点 ( $y_n,\; n = 1, 2, \ldots , 10$ ) .

MATLAB 
d = [-1.10 -0.40 -0.20 -0.02 0.02 0.71 1.35 1.46 1.74 3.89]';

コーシー分布のPDFとこのデータに対する尤度, 対数尤度 ( 定数項除く ) は,

\begin{align}\large{ f(y \mid \mu, \tau^2) = \frac{1}{\pi} \frac{\tau}{(y - \mu)^2 - \tau^2} \notag \\ L(\mu, \tau^2) = \prod_{n = 1}^{10} \frac{1}{\pi} \frac{\tau}{(y_n - \mu)^2 - \tau^2} \notag \\ \ell(\mu, \tau^2) = 10 \log(\tau) - \sum_{n = 1}^{10} \log{\{ (y_n - \mu)^2 - \tau^2 \}} \notag }\end{align}

最適化は, 今回メインテーマではないので, Optimization Toolboxで楽をする.

MATLAB 
d = [-1.10 -0.40 -0.20 -0.02 0.02 0.71 1.35 1.46 1.74 3.89]';　% データ
% 対数尤度をデータを含む函数として定義, 最小化問題にするためにマイナスをつけた. 　　
f = @(x, d) -5*log(x(2)) + sum(log((d - x(1)).^2 + x(2)));　		
fun = @(x)f(x, d);                                             % データは定数として無名函数を再定義 
options = optimoptions('fminunc','Algorithm','quasi-newton');　% 最適化のオプション, 準ニュートン法を指定
options.Display = 'iter';　                                    % イテレーション毎に情報を出力希望
x0 = [0, 1];　                                                 % 初期値
[x, fval, exitflag, output] = fminunc(fun, x0, options);　     % 最適化開始

%　結果
Iteration  Func-count       f(x)        Step-size       optimality
0           3             7.74278                             2.11
1           9             7.26691        0.186365            0.471  
2          12             7.22646               1             0.29  
3          15             7.19786               1            0.244  
4          18             7.19271               1           0.0627  
5          21             7.19224               1          0.00731  
6          24             7.19224               1         0.000651  
7          27             7.19224               1          4.7e-05  
8          30             7.19224               1         1.97e-06  

Local minimum found.

>> x
x = 0.2675    0.6052

教科書の表4.3と同じ結果となった. パラメータに関する導関数が０となっていることなども本当は確認すべきだろう. また, 最適化パフォーマンスを上げるために導関数やヘシアンをMATLABに陽に与える方法については, コチラ.

太陽黒点数データに最適なBox-Cox変換をAICにより選ぶ

AIC ( 赤池情報量基準 )

\begin{align}\large{ \mathrm{AIC} = -2\ell(\hat{\theta}) + 2k \notag }\end{align}
ここで, $\ell(\hat{\theta})$ は最大対数尤度, $k$ はパラメータ数である.

Box-Cox 変換

Box-Cox 変換は以下の式で与えられる.

\begin{align}\large{ z_n = \left\{\begin{array}{ll} \lambda^{-1}(y_n^\lambda - 1) & (\lambda \neq 0) \\ \log{y_n} & (\lambda = 0) \end{array}\right. 　\notag 　　}\end{align}
つまり,
  • $\lambda = -1$ なら逆数,
  • $\lambda = 0$ なら対数,
  • $\lambda = 0.5$ なら平方根,
  • $\lambda = 1.0$ なら現データ,
をとる.

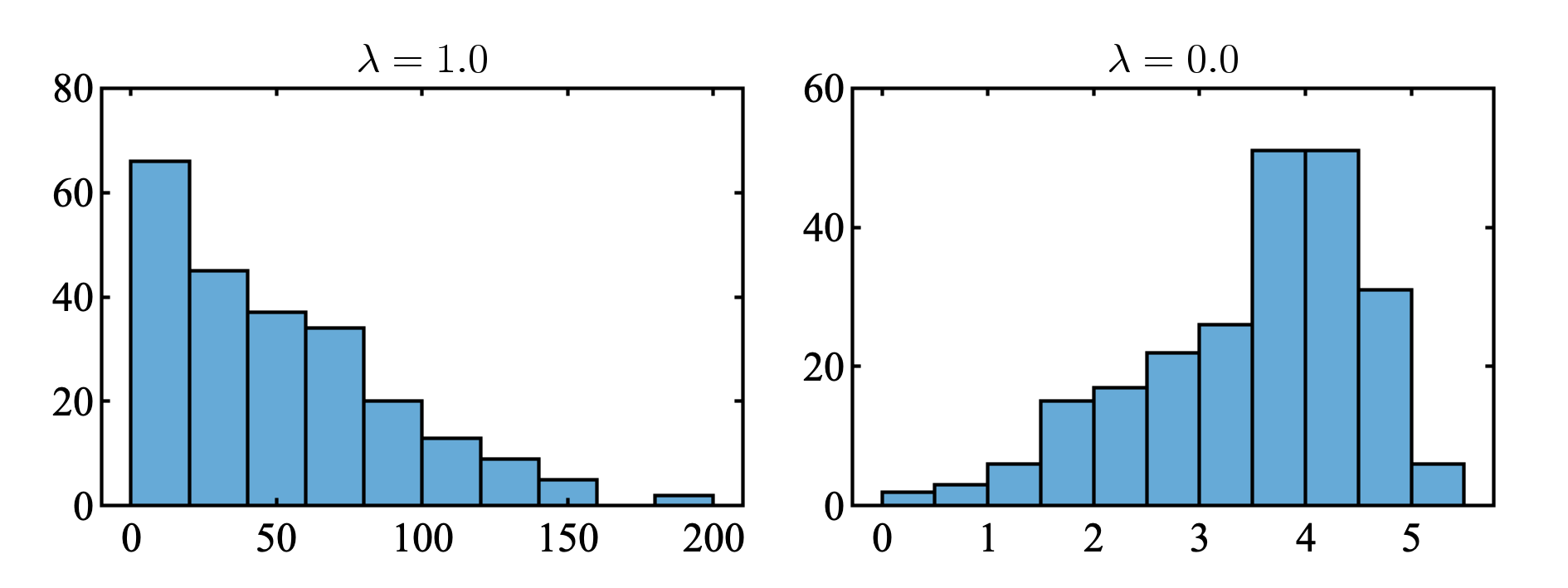
次の図は, 太陽黒点数データのヒストグラム ( 左図 ) , 対数をとったあとのヒストグラム ( 右図 ) である. どちらも, 到底正規分布しているとは言えないが, $\lambda$ をうまくとってBox-Cox変換すれば正規分布させれそうである.

name
MATLABコード MATLAB 
d = sunspot; 
t = tiledlayout(1, 2); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
histogram(d)
title('$\lambda = 1.0$','Interpreter','latex')

nexttile
histogram(log(d))
title('$\lambda = 0.0$','Interpreter','latex')

注意

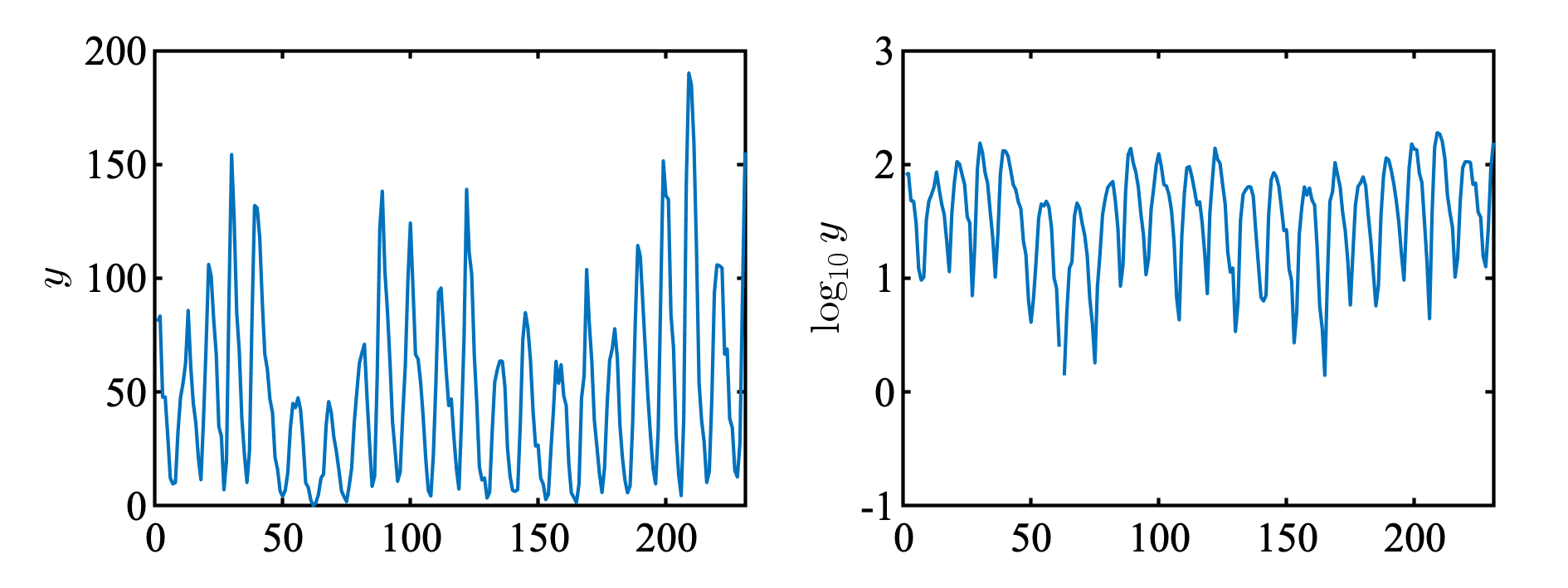
いかに, 太陽黒点数の原データ ( 左図 ) と底を10とした対数をとった図 ( 右図 ) を示す. 右図が教科書の図4.4と一致していることから, この教科書では, 底として10を使っているようである. 一方Box-Cox変換で使われている対数の底は $e$ が一般できであるようなので, 以下, Box-Cox変換では $e$ を底とする.

また, 太陽黒点数のデータには０が含まれている ( x軸55くらい, 右図ではNaNとなり表示されていない ) . しかし, 教科書の図4.4では, 底が10の対数で0.1となっている. それに合わせて, 以下でも値が0の点を$1.2589$ ( $= 10^{0.1}$ ) でおきかえた. なお, 0以下の値を含むデータにBox-Cox変換は適用できない.

name

いくつかMATLAB函数を用意する

最大対数尤度を返す函数

データを渡すと, 正規分布にあてはめたときの最尤パラメータ ( $\hat{\mu}, \hat{\sigma^2}$ ) を計算し, そのパラメータのときの対数尤度, つまり最大対数尤度を返す函数.

\begin{align} \mathrm{Likelihood} = \prod_{n = 1}^{N} \mathcal{N}(\mu, \sigma^2) \notag \\ \end{align}
\begin{align} \ell({\hat{\mu}, \hat{\sigma^2}}) = -\frac{N}{2}\log{2\pi} - N\log{\hat{\sigma}} - \frac{1}{2 \hat{\sigma^2}} \sum_{n = 1}{N}(y_i - \hat{\mu})^2 \notag \end{align}

MATLAB 
function l = maxLogLikelihood4normal(d)

N      = length(d);
mu     = mean(d);
sigma2 = var(d, 1); % 最尤推定量なのでNでわる！

% calc loglilelihood

A = -0.5 * N * log(2*pi);
B = -N * log(sqrt(sigma2));
C = -0.5 * sum((d - mu).^2) / sigma2;
l = A + B + C;

end

Box-Cox変換を行いAICを返す函数

パラメータ $\lambda$ とデータを渡すと, Box-Cox変換を行いAIC ( 教科書でいう $ \mathrm{AIC}_z^{\prime}$ ) を返す函数.

MATLAB 
function [z, AICz] = myBoxcox(d, lambda)

if lambda ~= 0
    z = (d.^lambda - 1)/lambda;
    j = -2 * sum(log(abs(d .^ (lambda-1))));
else
    z = log(d);
    j = -2 * sum(-log(abs(d)));
end

l = maxLogLikelihood4normal(z);
AIC = -2*l +2*2;
AICz = AIC + j;

end

$\lambda$ 選択

$\lambda$ を-1から1まで0.2刻みで変えて, AICをみてみる.

MATLAB 
d = sunspot;
d(d==0) = 10^0.1;

lambdas = -1:0.2:1;
aics = zeros(1, length(lambdas));
for I = 1:length(lambdas)
    
    [z, AICz] = myBoxcox(d, lambdas(I));
    aics(I) = AICz;
end

bar(lambdas, aics)
xlabel('$\lambda$','Interpreter','latex')
ylabel('AIC')
ylim([2000 3000])
xticks(lambdas)
name

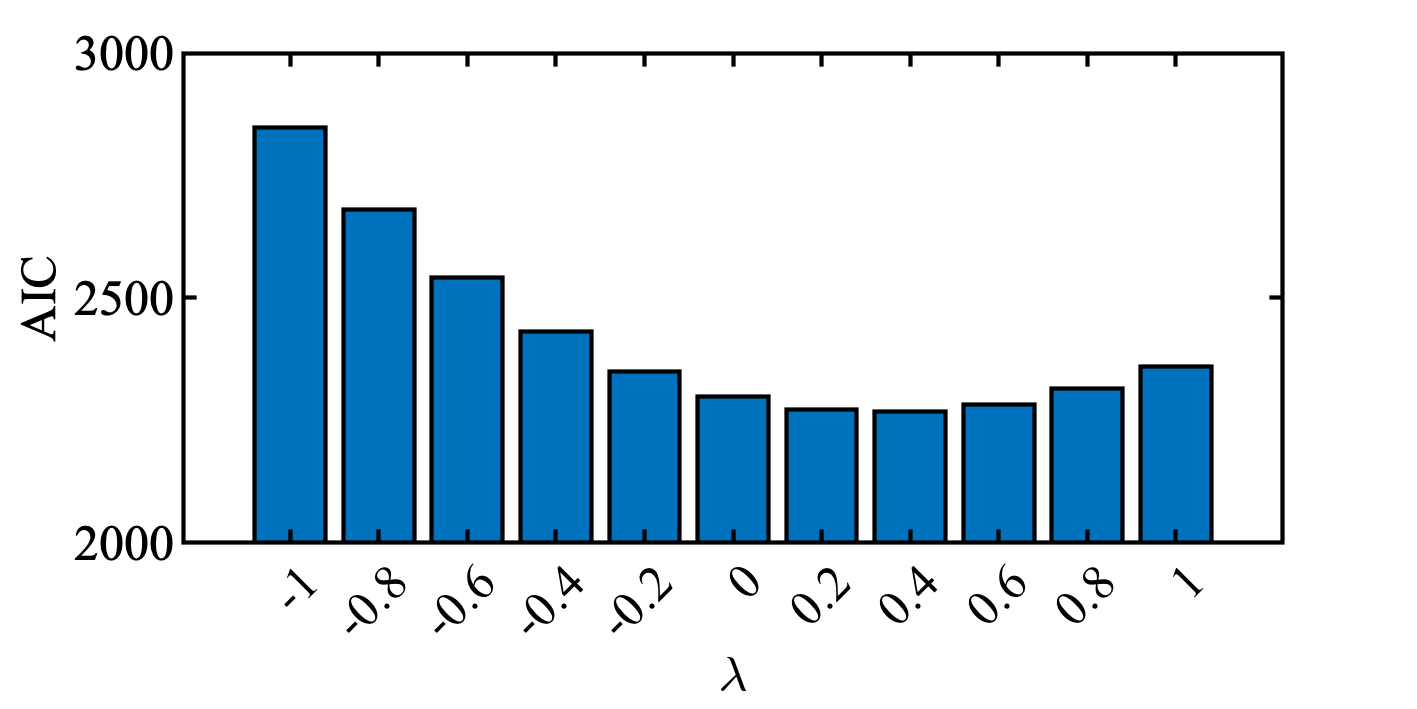
教科書と結構違う結果となってしまった. 計算を間違えたかと思って, 実際にBox-Cox変換を行い, ヒストグラムをみてみた. 僕の計算だと $\lambda = 0.4$ が選ばれて, 教科書では $\lambda = -0.2$ が選ばれている.

name

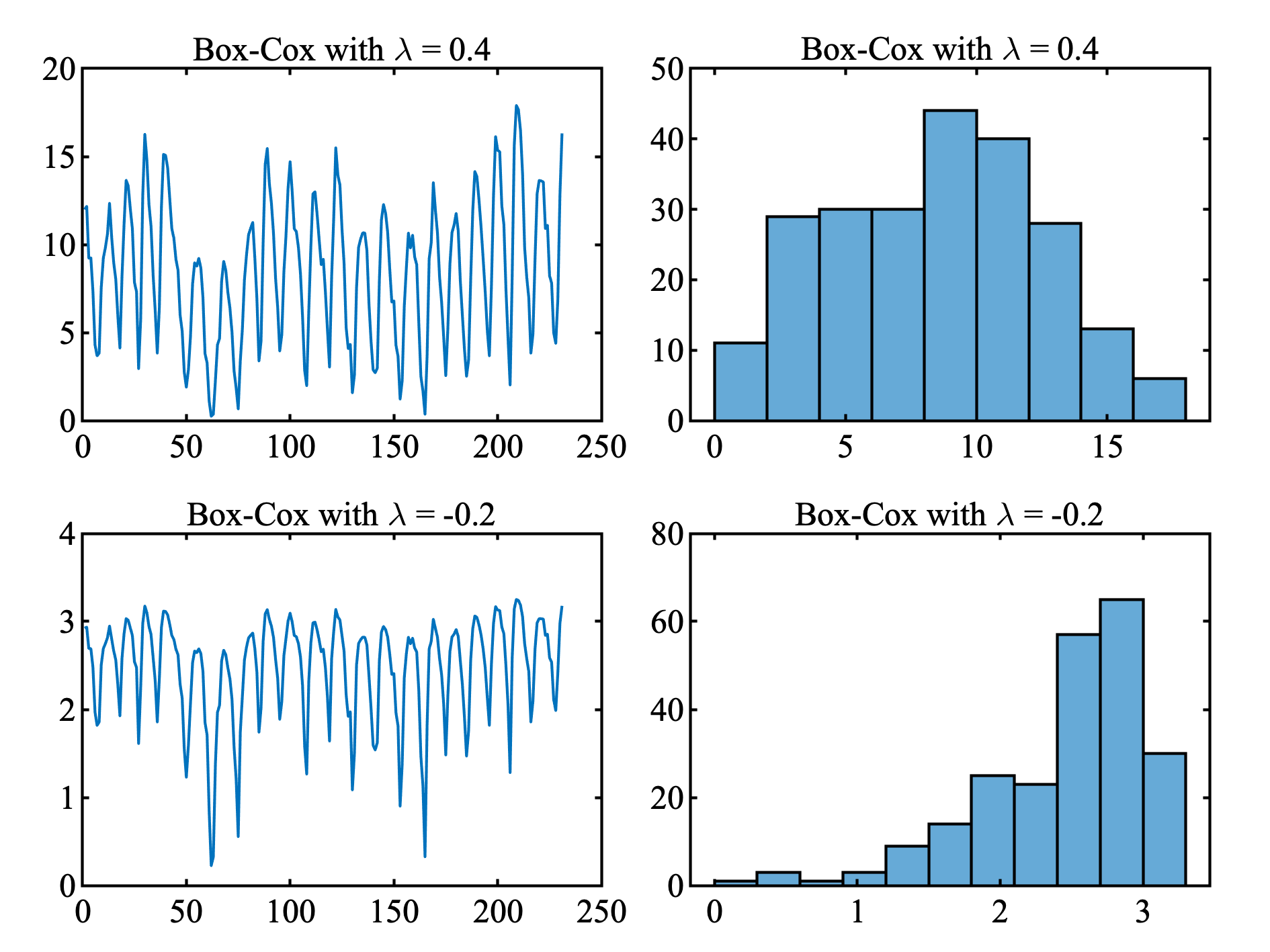
$\lambda = 0.4$ がよいように見える. どういうことなんだ.

一応自分の或るデータでもやってみた. $\lambda = -1.5$ が選ばれた.

name

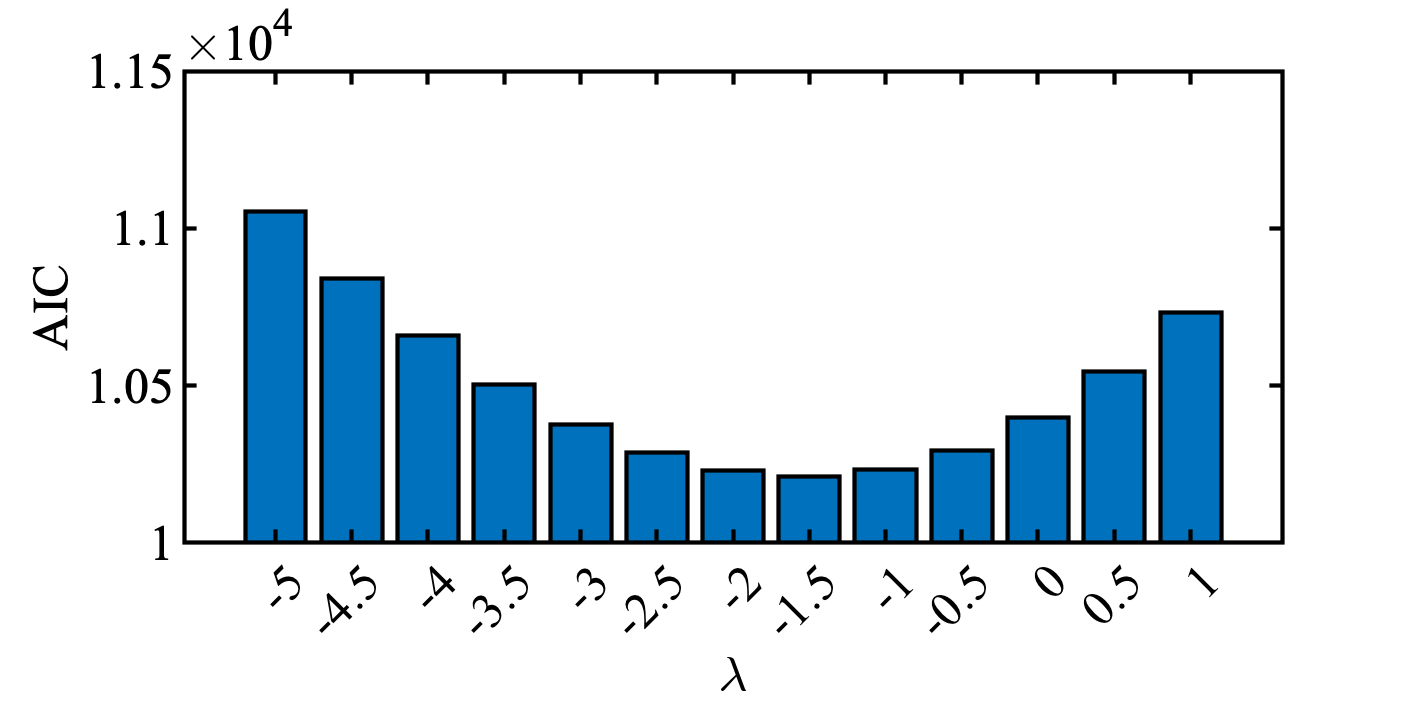
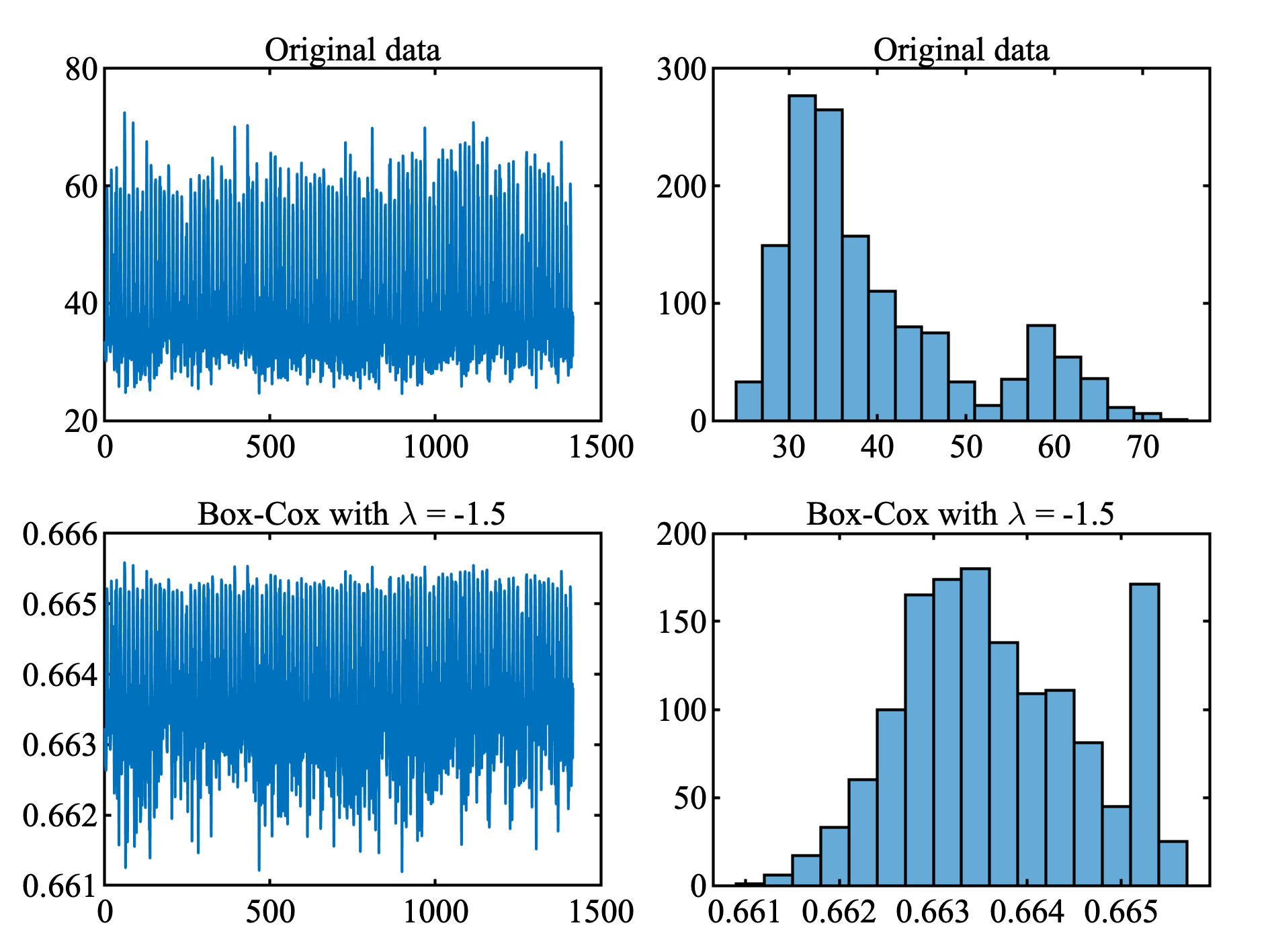
原データと, 変換後のデータ, それぞれのヒストグラムを見比べてみる. 正規分布に近づいてるんじゃないですか？ でっぱりがめちゃくちゃきになるけど.

name

Yeo–Johnson transformation

Box-Cox変換は正数データにしか適用できなかった. この欠点を修正したYeo–Johnson transformationというものがあるらしい[1].

\begin{align}\large{ \psi(\lambda, x) = \left\{\begin{array}{llll} \{ (x+1)^\lambda - 1 \} / \lambda & (x \geq 0,\;\lambda \neq 0) \\ \log{(x+1)} & (x \geq 0,\;\lambda = 0) \\ -\{ (-x+1)^{(2-\lambda)} - 1 \}/(2-\lambda) & (x \lt 0,\;\lambda \neq 2) \\ -\log{(-x+1)} & (x \lt 0,\;\lambda = 2) \end{array}\right. 　\notag 　　}\end{align}

主な参考文献


[1] In‐Kwon Yeo, Richard A. Johnson: Biometrika, Volume 87, Issue 4, December 2000, Pages 954–959,

この記事のTOP    BACK    TOP