MATLABで『時系列解析入門』３章

最終更新：2021/07/21

非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

3.1 スペクトル

白色雑音のスペクトル

白色雑音 ( ここでは, 平均０分散１の正規分布に従う ) を作ってみる. また, ”標本”自己相関関数.

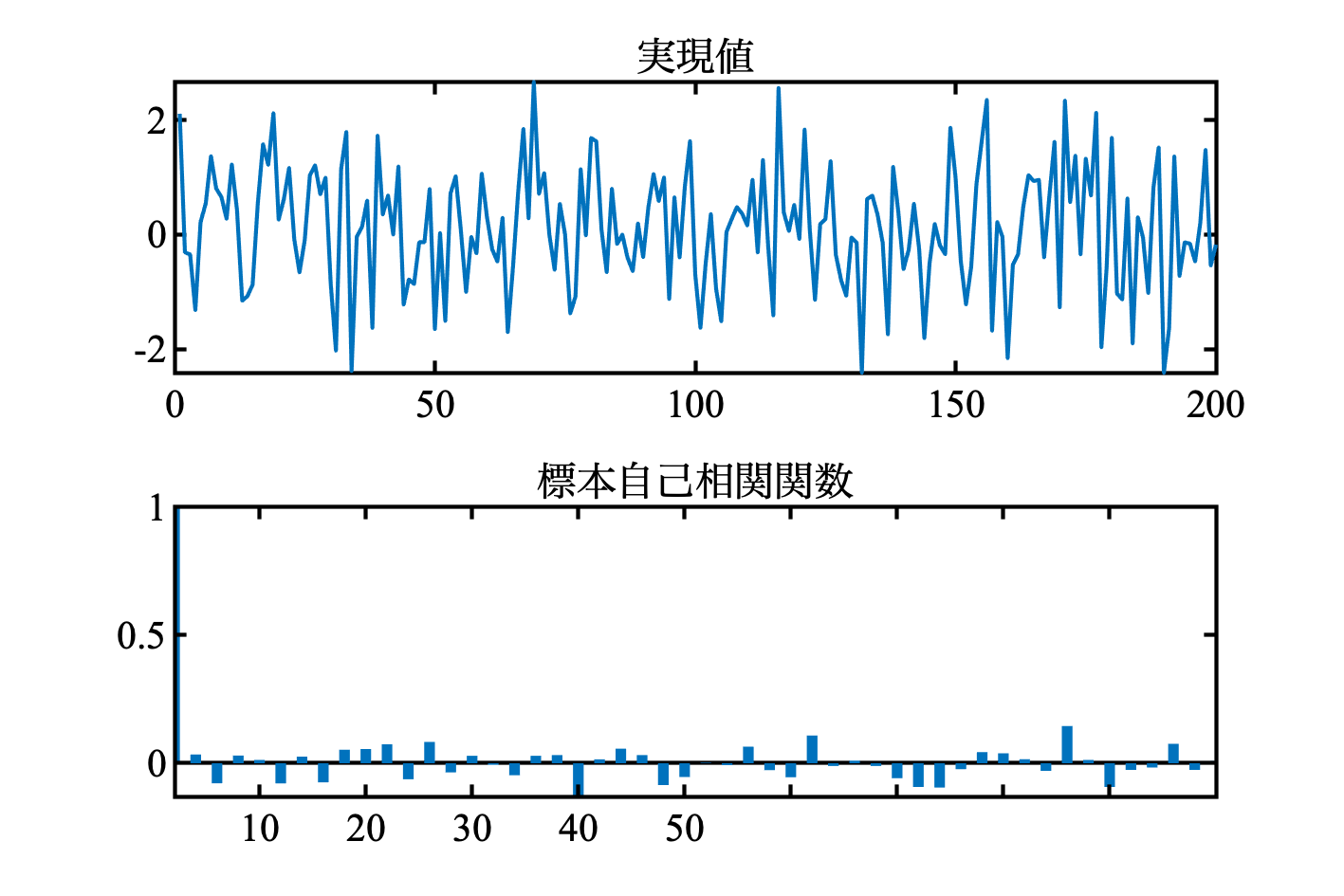
MATLABコード

MATLAB

N = 200;
rng(12345); y = randn(N, 1); 

subplot(211); 
plot(y)
title('実現値')

subplot(212); 
bar(xcorr(y, 50, 'normalized'), 0.5); xlim([1+N/4 N/2])
title('標本自己相関関数')
xticklabels(10:10:50)

いい感じ. 標本自己相関関数も教科書図3.1(a)と似ている.

1次自己回帰モデルのスペクトル

モデル

\begin{align}\large{ y_n = ay_{n-1} + w_n, \quad w_n \sim \mathcal{N}(0, \sigma^2) \notag }\end{align}

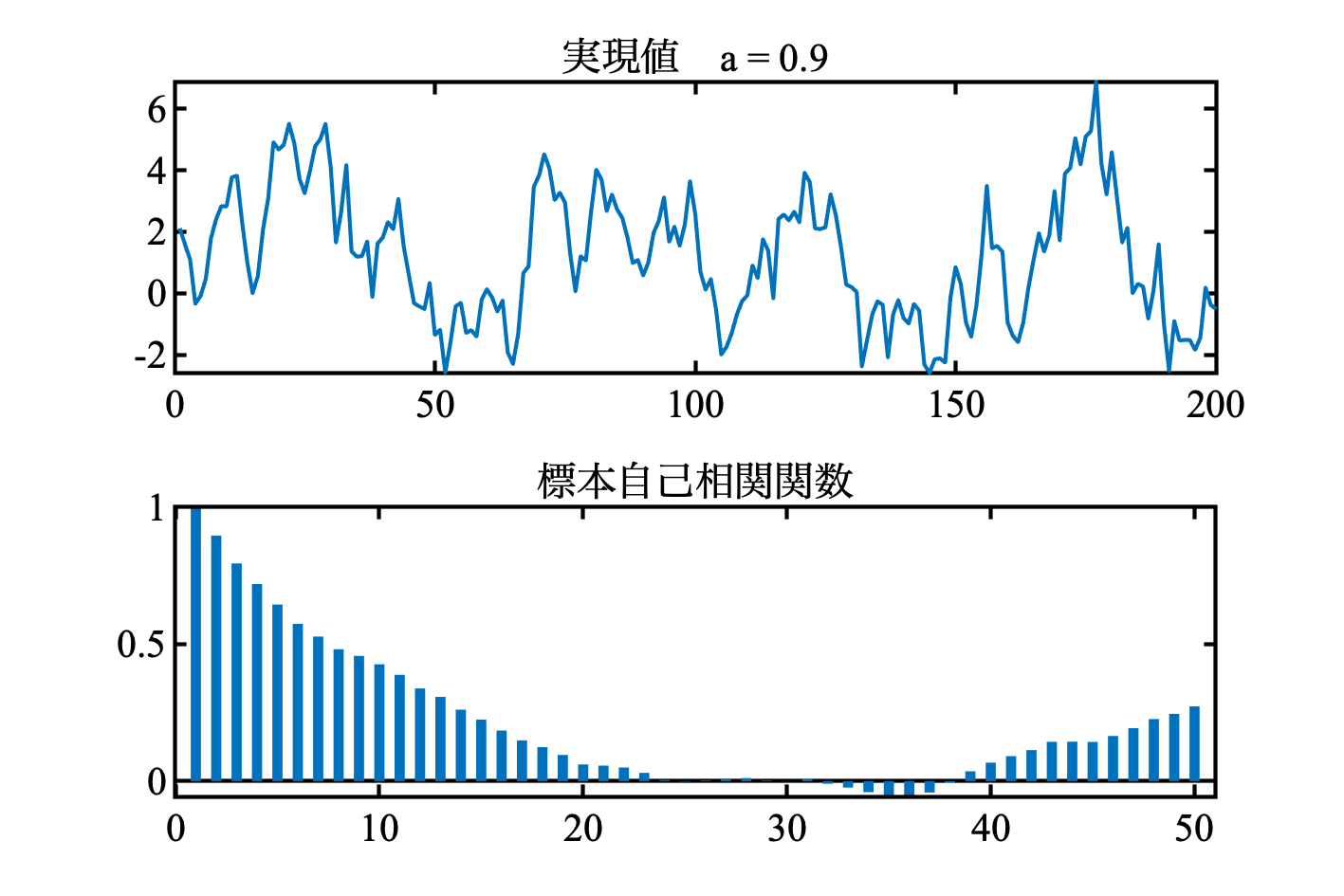
MATLABコード

MATLAB

N      = 200;
a      = -0.9;
sigma2 = 1.0;

rng(12345)
sigma = sqrt(sigma2); 
y = zeros(N, 1);
y(1) = sigma*randn();
for n = 2:N
    y(n) = a*y(n-1) + sigma*randn();
end
subplot(211)
plot(y)
title(['実現値    a = ' num2str(a)])

subplot(212)
xc = xcorr(y, 50, 'normalized');
bar(1:N/4, xc(N/4+1:N/2), 0.5, 'LineStyle', 'none'); 
title('標本自己相関関数')

標本自己相関関数は後半上がっているが, これは偶然. 教科書図3.2(a)と誤差があるが, 乱数をかえていろいろみてみると, これくらいの規模の誤差は生まれるよう.

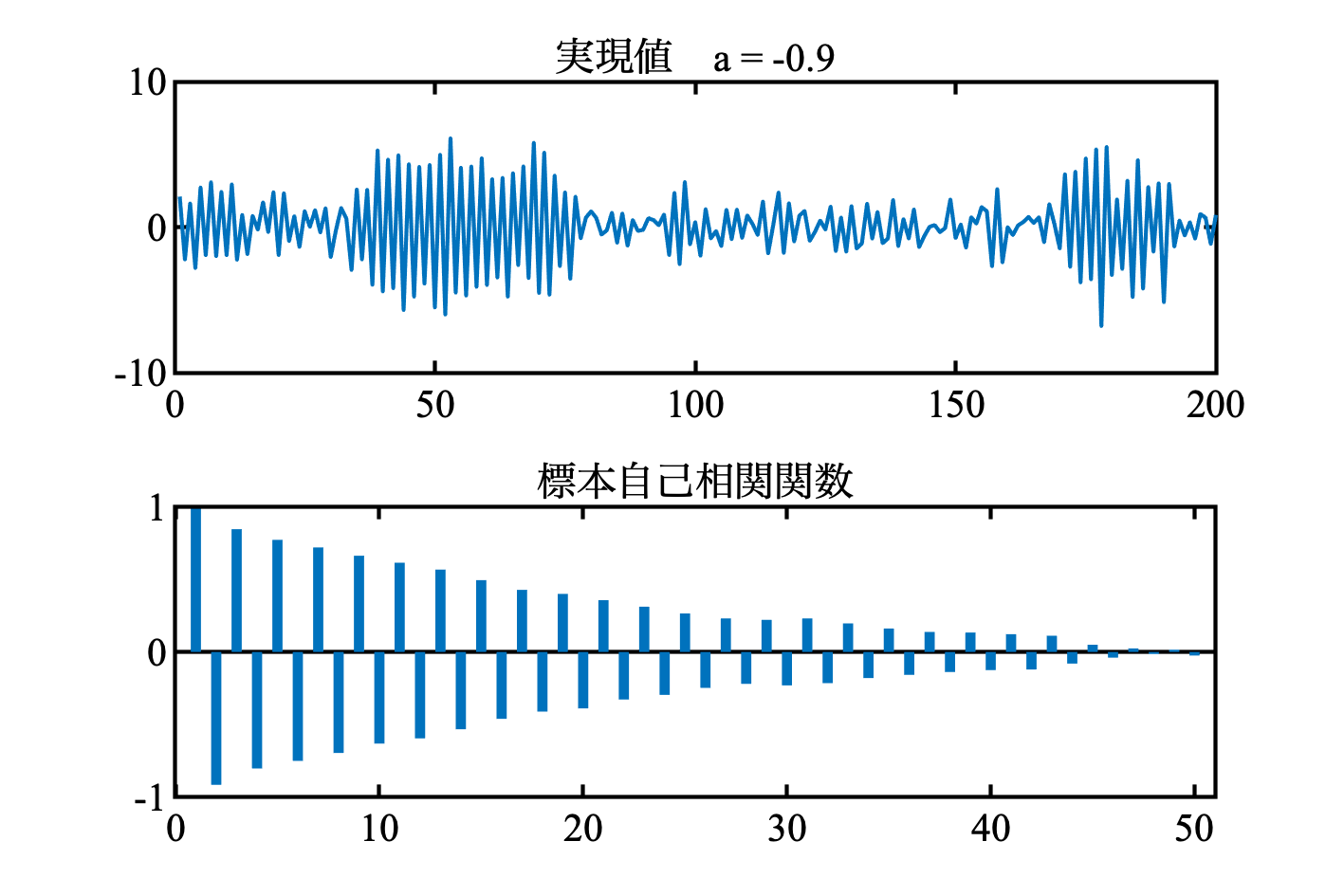
次は, $a = -0.9$ としてみた. 教科書図3.3と見比べてほしい.

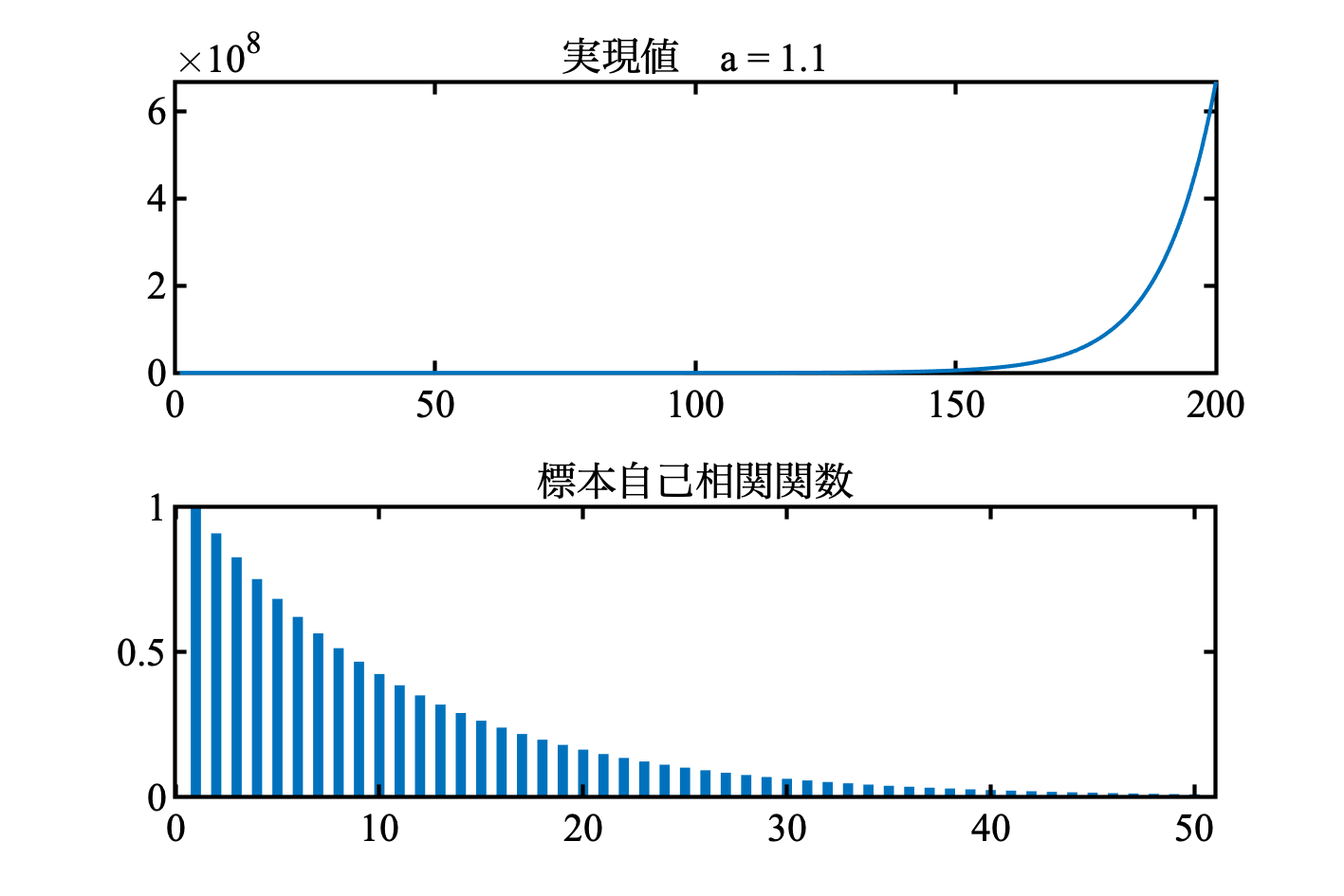
ちなみに $|a| > 1.0$ となると発散する ( $a$ がどんどんかけられるのだから当然 ). $a = 1.1$ の結果を示す.

標本自己相関関数は, 非定常時系列に現れがちな形になっている.

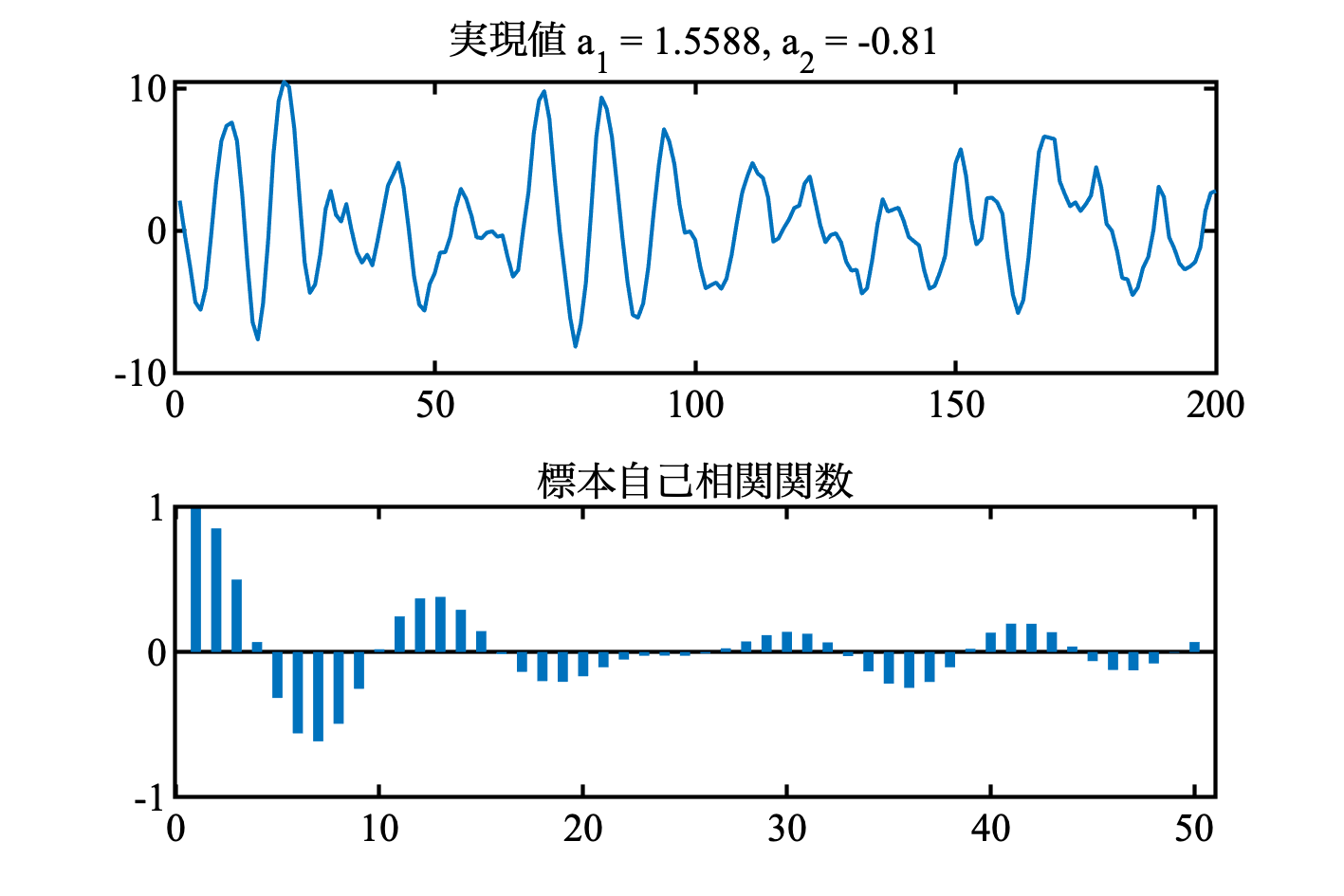
2次自己回帰モデルのスペクトル

モデル

\begin{align}\large{ y_n = a_1y_{n-1} + a_2y_{n-2} + w_n, \quad w_n \sim \mathcal{N}(0, \sigma^2) \notag }\end{align}

MATLABコード

MATLAB

N      = 200;
a1     = 0.9*sqrt(3);
a2     = -0.81;
sigma2 = 1.0;

rng(12345)
sigma = sqrt(sigma2); 
y = zeros(N, 1);
y(1) = sigma*randn();
y(2) = sigma*randn();

for n = 3:N
    y(n) = a1*y(n-1) + a2*y(n-2) + sigma*randn();
end
subplot(211)
plot(y)
title(['実現値 a_1 = ' num2str(a1), ', a_2 = ' num2str(a2)])

subplot(212)
xc = xcorr(y, 50, 'normalized');
bar(1:N/4, xc(N/4+1:N/2), 0.5, 'LineStyle', 'none'); 
title('標本自己相関関数')

いろいろな $a_1$, $a_2$ を入れてもらったらわかるが, すぐに発散する. なかなかいい値を見つけるのは難しい. 詳しいことは後の章ででてくる.

ピリオドグラム

p.38 の計算法

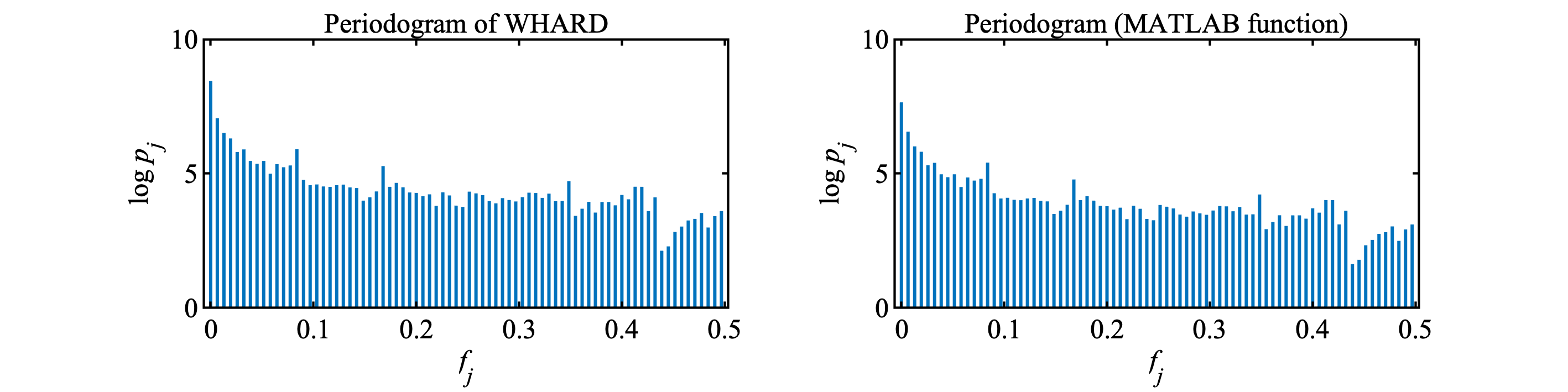
p.38式(3.8)で与えられているピリオドグラムの定義に従って計算してみる.

\begin{align}\large{ p_j = \hat{C_0} + 2 \sum_{k = 1}^{N-1} \hat{C_k} \cos{2 \pi k f_j},\quad f_j = j/N, \; f_j = 0, 1, \ldots, [N/2]. \notag }\end{align}

ただし, $[\cdot]$ は床関数. これを, WHARDデータに適用してみる. 桁が結構教科書の図 ( p.33図3.5e ) と違うが形はおおよそあっている. 念の為, MATLABのSignal Processing Toolboxにあるperiodogramも使って確認した. だいたい, 桁があっている.

注意.

$p_0$ が0となるので, データから平均はひいていない.
教科書の $\log{p(f)}$ と桁が合わない. しかし, 形は合ってるし, MATLAB函数とはよく合っているのでよしとした.
$\log{}$ の底は10としている.

ところで, MATLABのインデクシングが1始まりなのは, 結構時系列解析では頭を混乱させるね.

MATLAB

function [p, fj] = myPeriodogram(d)

d = reshape(d, [], 1);
N = length(d);

Chat  = xcorr(d)/N;
Chat  = Chat(N:end); 
C0hat = Chat(1); 
Chat  = Chat(2:end);
K     = 1:N-1;

p = zeros(floor(N/2)+1, 1);
for j = 0:floor(N/2)
   a =  2*cos(2*pi*K*j/N); 
   p(j+1)  = C0hat + sum(a .* Chat); 
end
fj = (0:floor(N/2))/N;

end

MATLAB

d = whard;
% d = d - mean(d);

% 教科書の式を用いたピリオドグラムのプロット
[p, fj] = myPeriodogram(d);

subplot(121)
bar(fj, log10(p), 0.5, 'LineStyle', 'none')
ylim([0 10])
xlabel('\it{f_j}')
ylabel('log \it{p_j}')
title('Periodogram of WHARD')

% MATLAB函数を用いたピリオドグラムのプロット
nfft = length(d);
[pxx,w] = periodogram(d, [], nfft); % 教科書の式と点数を合わせるため, 点数の指定をした. 


subplot(122)
bar(fj, log10(pxx), 0.5, 'LineStyle', 'none')
ylim([0 10])
xlabel('\it{f_j}')
ylabel('log \it{p_j}')
title('Periodogram (MATLAB function)')

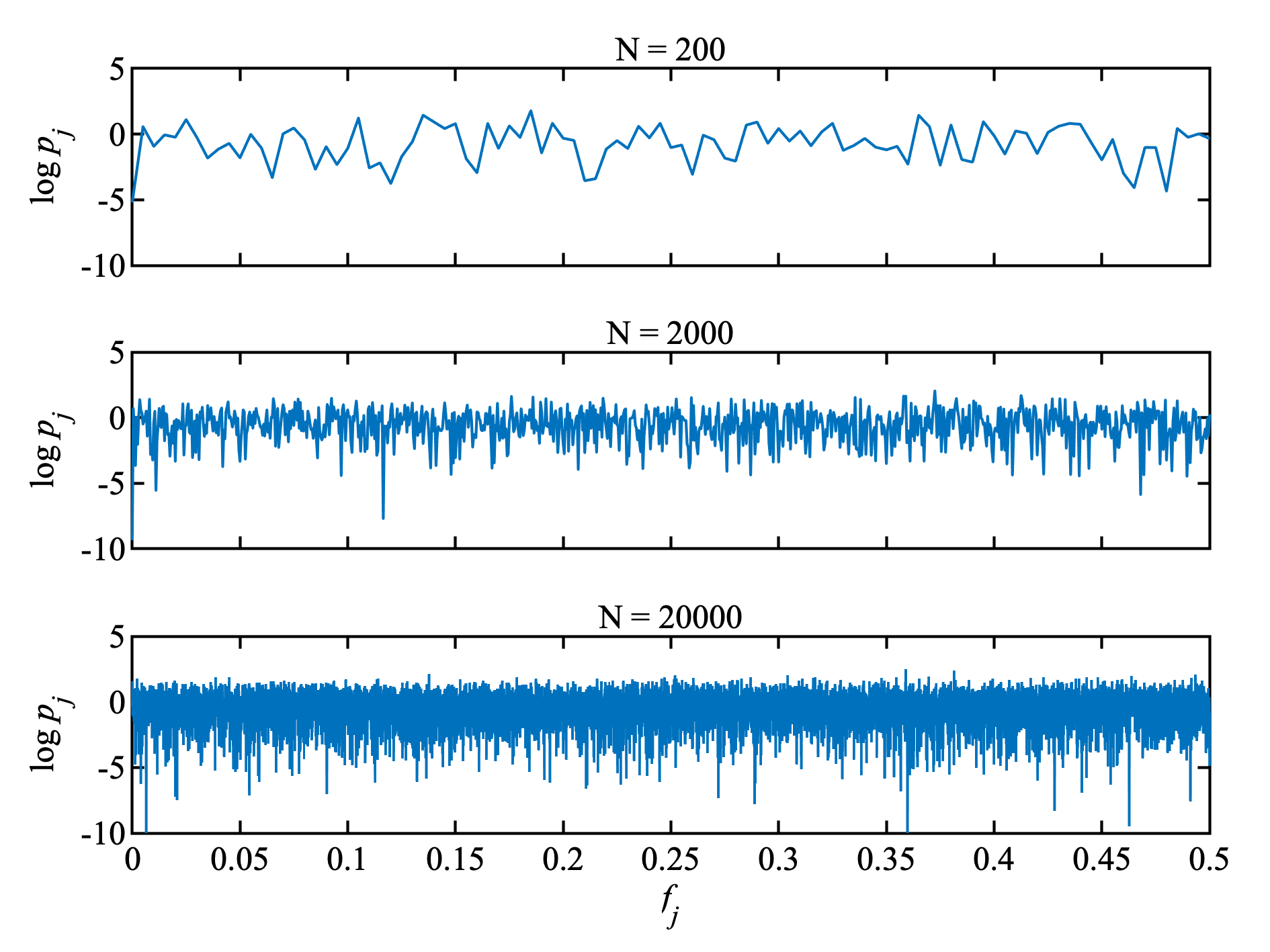
ピリオドグラムは一致推定量ではない

ピリオドグラムは, 真のスペクトラム $p(f)$ に対する普遍性をもっているが, 一致性はない. つまり, いくらデータをふやしたところで, ピリオドグラムが $p(f)$ に収束することはない.

白色雑音で確かめてみる. 確かに, $N$ をいくら増やしても, 分散はかわらない. もし, 一致性があれば, $N$ を増やすと真のスペクトルである $\log{(p_j)} = 0$ の近い所をうろつくはずである.

MATLABコード

MATLAB

Ns = [200 2000 20000];
t = tiledlayout(3, 1);
for I = 1:3
    nexttile
    d = randn(Ns(I), 1);
    [p, fj] = myPeriodogram(d');
    plot(fj, log(p))
    if I ~= 3; xticklabels({}); end
    ylabel('log \it{p_j}')
    ylim([-10 5])
    title(['N = ' num2str(Ns(I))])
end
nexttile(3)
xlabel('\it{f_j}')
t.TileSpacing = 'compact';
t.Padding = 'compact';

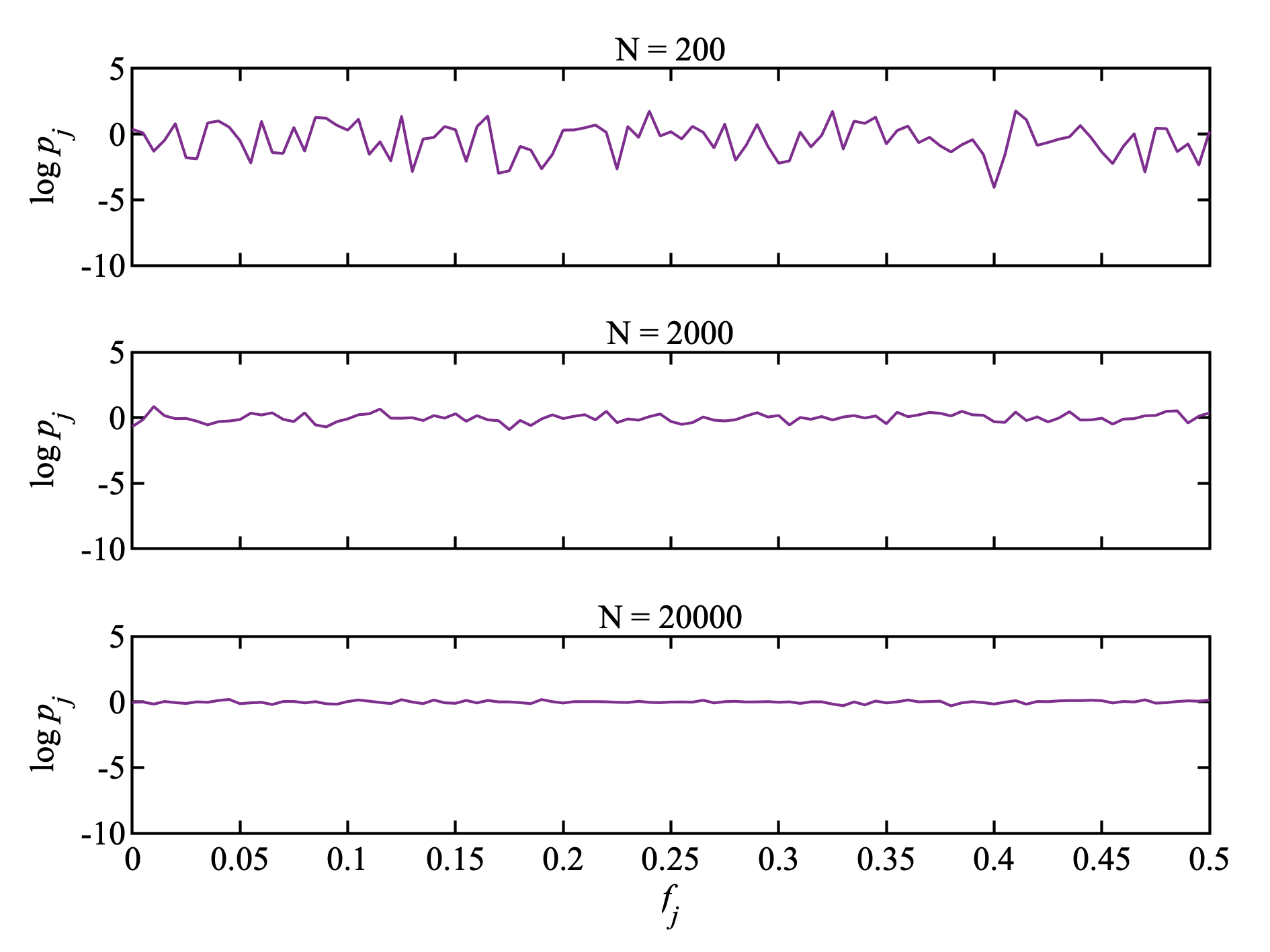
ピリオドグラムの平均と平滑化

生スペクトル

真のスペクトルに収束するような推定量を求める. 教科書では二通りの求めかたが載っているが, 直感的にわかりやすい,

\begin{align}\large{ p_j = \frac{L}{N}\sum_{i = 1}^{N/L} p_j^{(i)} \notag }\end{align}

を使う. つまり, データを $L$ 個ずつにわけてピリオドグラムを計算し, その平均をとる.

前の図と同じ計算 ( ホワイトノイズのピリオドグラム ) を, $L = 200$ ずつに区切っておこなってみた. つまり, 例えば $N = 2000$ の場合は, 10 本のピリオドグラムの平均である. $N$ がふえるにつれ, $\log{(p_j)} = 0$ への収束がよくなっている.

MATLABコード

MATLAB

Ns = [200 2000 20000];
L = 200;
t = tiledlayout(3, 1);
for I = 1:3
    nexttile
    d = randn(Ns(I), 1)';
    p = zeros(floor(L/2)+1, 1);
    for l = 1:Ns(I)/L
        [pp, fj] = myPeriodogram(d(1+(l-1)*L:l*L));
        p = p + pp;
    end
    p = p/(Ns(I)/L);
    plot(fj, log(p))
    if I ~= 3; xticklabels({}); end
    ylabel('log \it{p_j}')
    ylim([-10 5])
    title(['N = ' num2str(Ns(I))])
end
nexttile(3)
xlabel('\it{f_j}')
t.TileSpacing = 'compact';
t.Padding = 'compact';

ハニングウィンドウによる平滑化

船舶の方向角速度で試してみる. まずは, 元データとピリオドグラム.

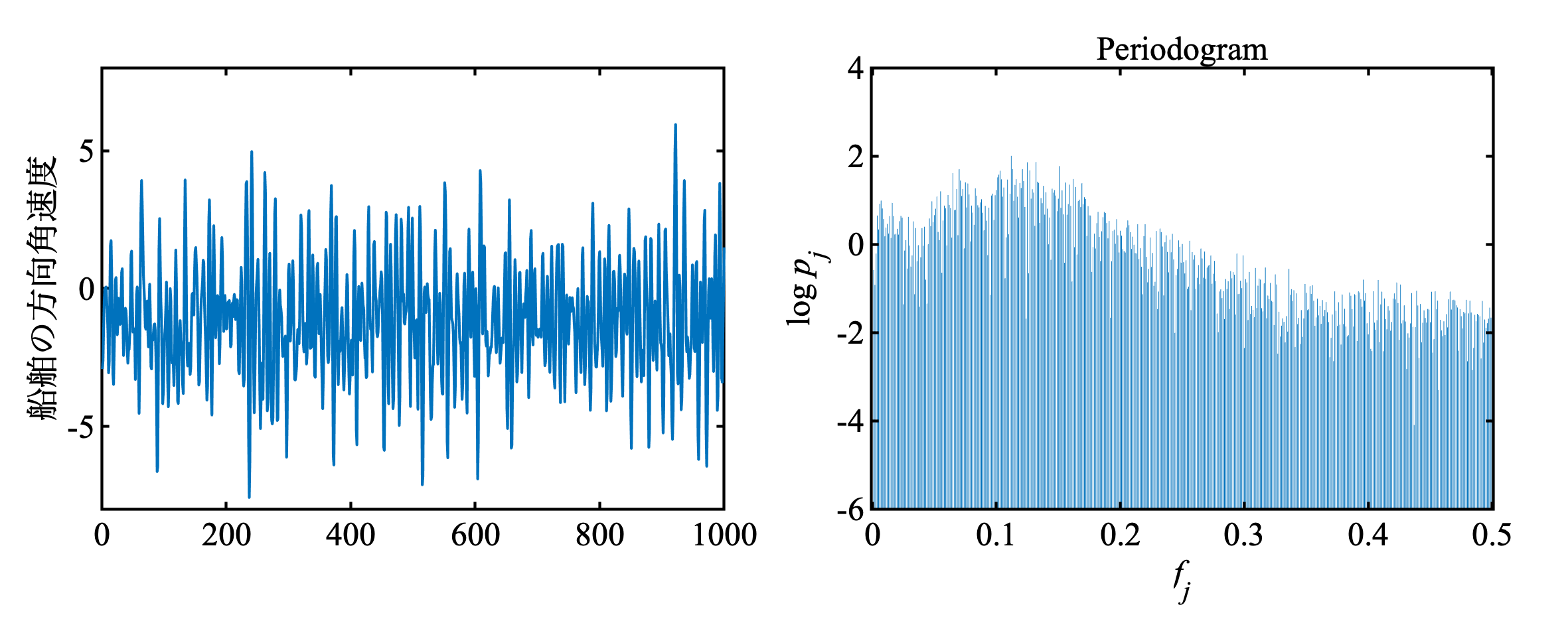
MATLABコード

MATLAB

d = hakusan.velocity;

t = tiledlayout(1, 2);
nexttile
plot(d)
ylabel('船舶の方向角速度')
ylim([-8 8])

nexttile
[p, fj] = myPeriodogram(d);
bar(fj, log10(p), 0.5, 'LineStyle', 'none', 'BaseValue', -6);
xlabel('\it{f_j}')
ylabel('log \it{p_j}')
title('Periodogram')
t.TileSpacing = 'compact';
t.Padding = 'compact';

次に, 時系列を長さ $L = [3 \sqrt{N}]$ ずつにわけて, 生ピリオドグラムを計算 ( 左図 ) . そして, $m = 1$ のハニングウィンドウで平滑化した. ウィンドウ $W_i\; (i = 0, \pm 1, \ldots, \pm m)$ を適用したスペクトル $\hat{p_j}$ は以下である.

\begin{align}\large{ \hat{p_j} = \sum_{-m}^{m} W_i p_{j-1}, \quad (j = 0, 1, \ldots, [L/2]). \notag }\end{align}

畳み込みだとおもうので, convを使った.

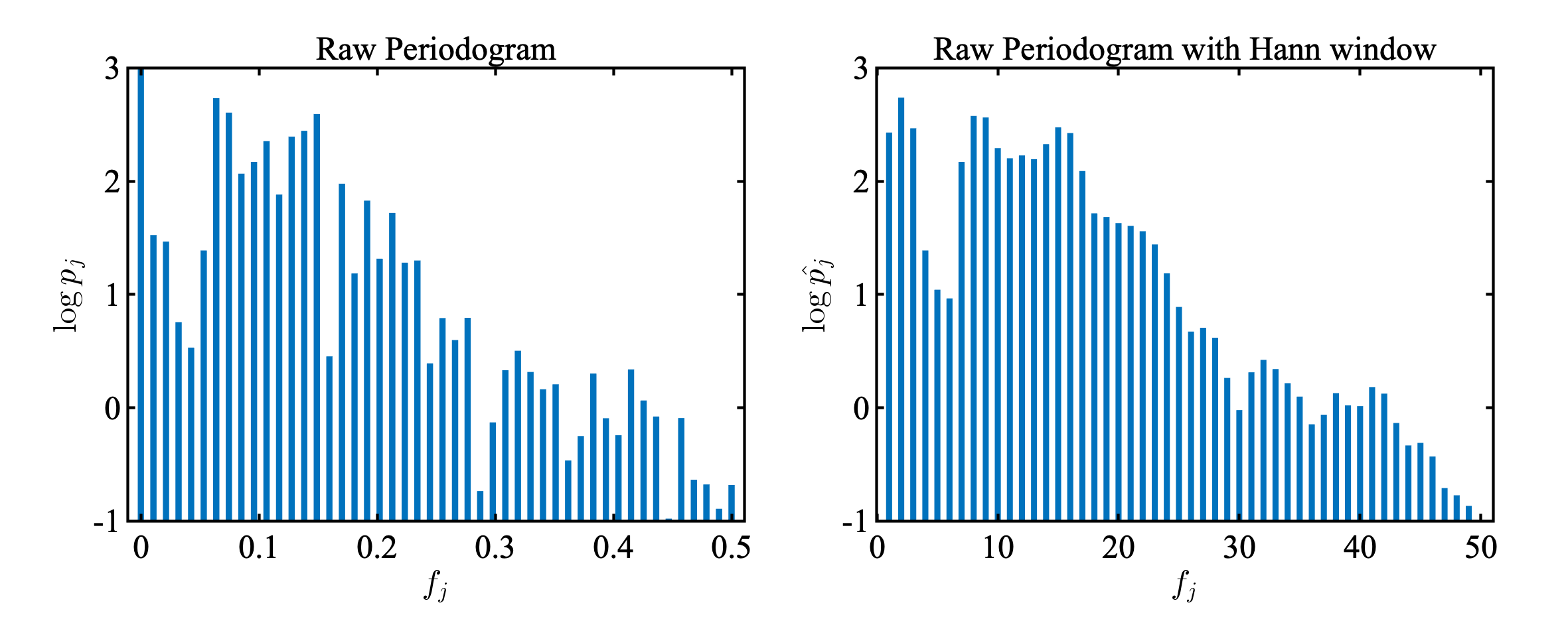
MATLABコード

MATLAB

d = hakusan.velocity;
L = floor(3*sqrt(length(d)));
l = floor(length(d)/L);

p = zeros(floor(L/2)+1, 1);
for I = 1:l 
    [pp, fj] = myPeriodogram(d(1+(l-1)*L:l*L));
    p = p + pp;
end

t = tiledlayout(1, 2);
nexttile
bar(fj, log10(p), 0.5, 'LineStyle', 'none', 'BaseValue', -6);
xlabel('$f_j$','Interpreter','latex')
ylabel('$\log{p_j}$','Interpreter','latex')
title('Raw Periodogram')
ylim([-1 3])

nexttile
p = conv(p, [0.25 0.5 0.25]);
bar(log10(p), 0.5, 'LineStyle', 'none', 'BaseValue', -6);
xlabel('$f_j$','Interpreter','latex')
ylabel('$\log{\hat{p_j}}$','Interpreter','latex')
title('Raw Periodogram with Hann window')
ylim([-1 3])

t.TileSpacing = 'compact';
t.Padding = 'compact';

教科書とちょっと違うけどこんなもんかねえ.

主な参考文献

この記事のTOP BACK TOP