MATLABで『カルマンフィルタ』２章:ローカルレベルモデル

モデル

シンプルな単変量時系列を扱うモデル. 観測量を $y_1, \ldots, y_n$ とする. そして, 観測量は状態量 $\alpha_t$ にホワイトノイズ $\ve_t$ がのったもの, 状態量の更新も同様にホワイトノイズ $\eta_t$ が乗るとする. するとモデルは,

となる. ここで, 初期状態 $\alpha_t$ についての情報はないが, とりあえず平均 $a_1$, 分散 $P_1$ に従うとする.

フィルタリング

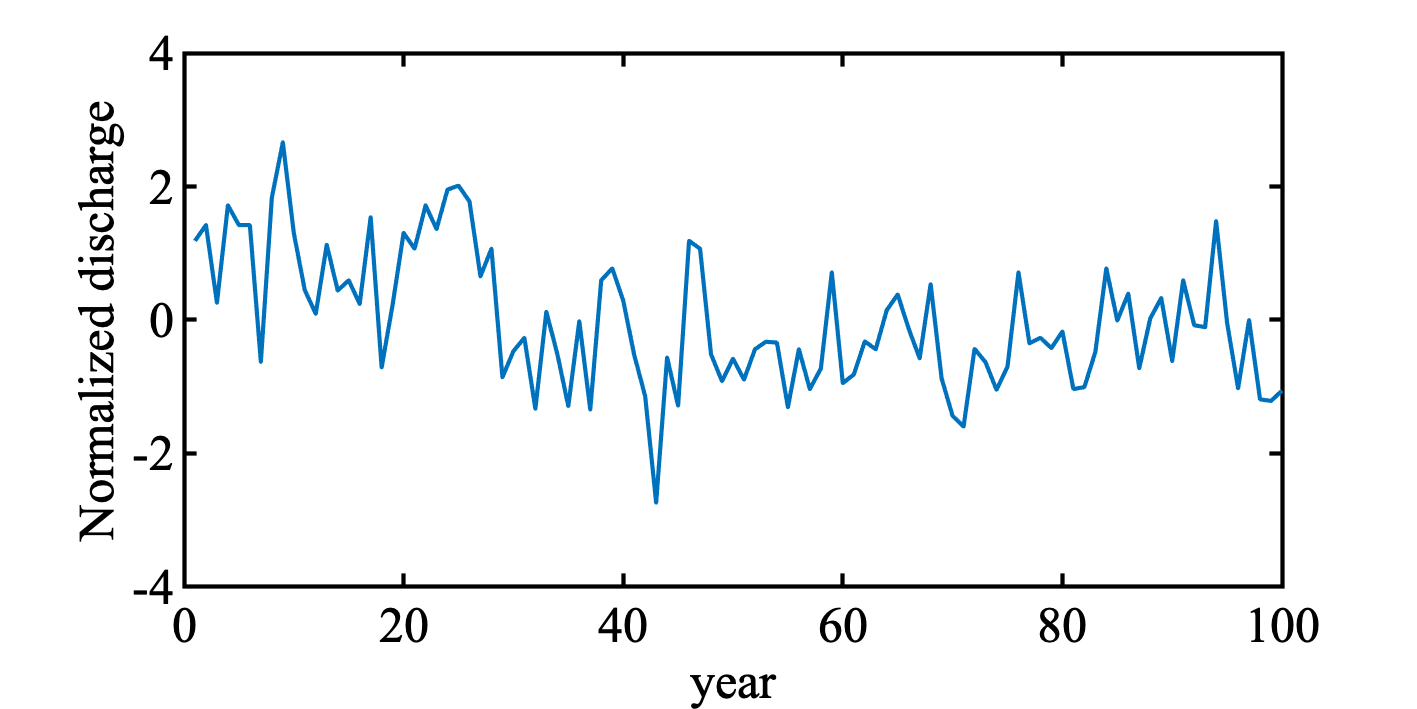
アルゴリズムを載せつつ, MATLABでコーディングしてみる. 対象データは有名なナイル川流量データ. Rに入ってるし, Kaggleとかからも取得可能. 便宜のため, 正規化した.

y = nile;
y = normalize(y);
plot(y)
xlabel('year'); ylabel('Normalized discharge')

アルゴリズム

アルゴリズムは以下のようになる. なお, $X_{\color{#cf201f}{t+1}|\color{blue}{t}}$ のような記述は, $\color{blue}{t}$ 期までの観測に基づく, $\color{#cf201f}{t+1}$ 期の $X$ の値の推定値という意味である.

ここで,

である. また,

と与えているので, 上のアルゴリズムは計算できる.

実装

実装するには, パラメータ $\sigma^2_\ve$, $\sigma^2_\eta$, $a_1$, $P_1$ を与えなければならないけれど, 今回はまず適当に与える. 以下のコードで, アルゴリズムとできるだけ文字と統一させた. 特に, $X_{t|t}$ のようなパラメータは, X_ttのように, $X_{t|t-1}$ のようなパラメータは, X_tt1のように記した.

y = nile;
y = normalize(y);
L = length(y);

% 適当に与える
varEps = 1;
varEta = 1;
a1 = 10;
P1 = 10;

% Preallocation
a_tt1 = zeros(size(y)); a_tt1(1) = a1;
P_tt1 = zeros(size(y)); P_tt1(1) = P1;
v_t   = zeros(size(y)); 
F_t   = zeros(size(y)); 
a_tt  = zeros(size(y)); 
P_tt  = zeros(size(y));
K_t   = zeros(size(y));

for t = 1:L
    
    % Innovation
    v_t(t) = y(t) - a_tt1(t);
    F_t(t) = P_tt1(t) + varEps;
    
    % Kalman gain
    K_t(t) = P_tt1(t)/F_t(t);

    % Current state
    a_tt(t) = a_tt1(t) + K_t(t)*v_t(t);
    P_tt(t) = P_tt1(t) * (1 - K_t(t));

    % Next state
    a_tt1(t+1) = a_tt(t);
    P_tt1(t+1) = P_tt(t) + varEta;
    
end

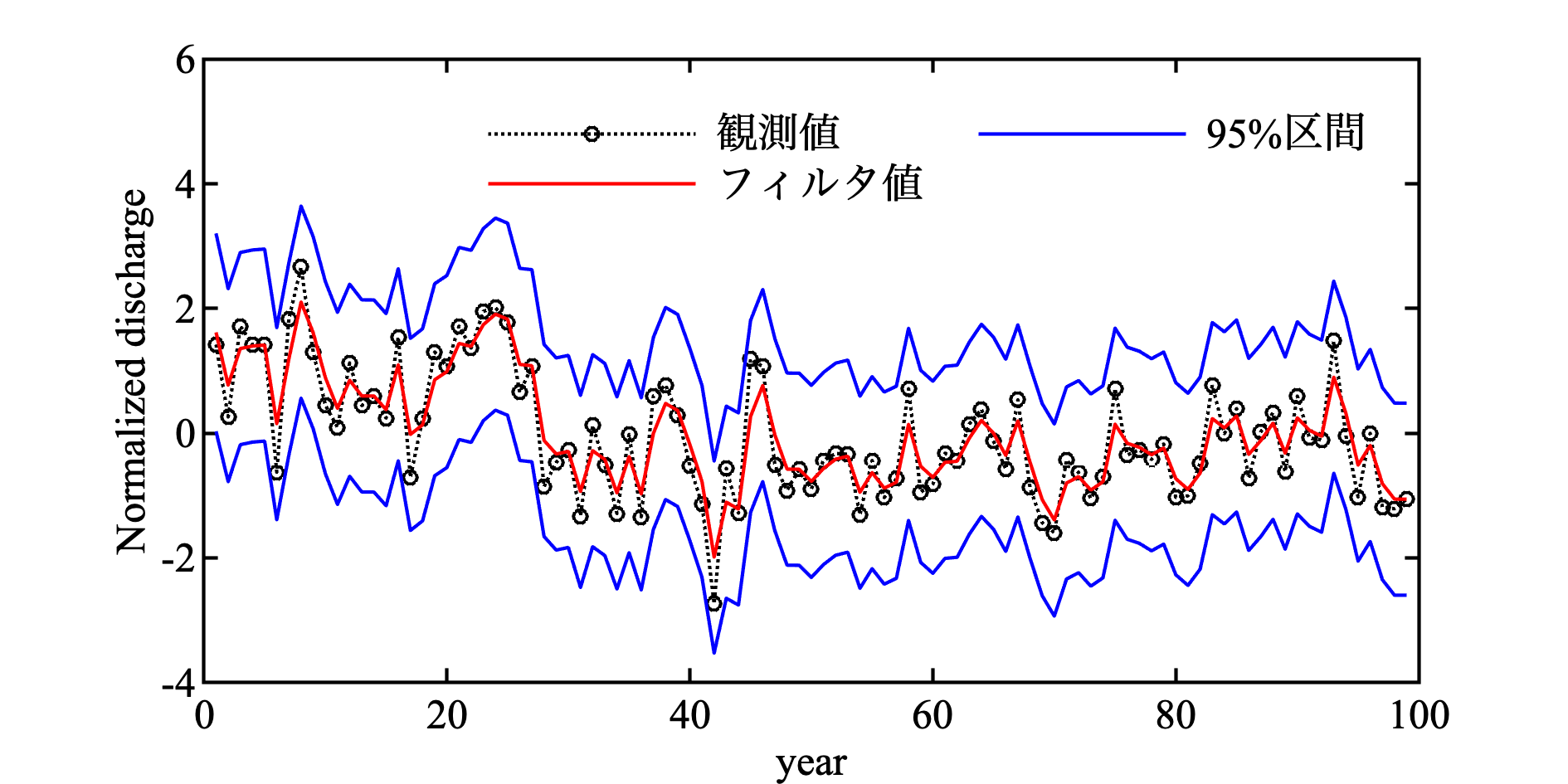
これで, フィルタリングが終わったので, 推定された状態（$a_{t|t}$）と, その95%区間（$a_{t|t} \pm 1.96 \sqrt{P_{t|t}}$）をみてみよう.

plot(y(2:end), ':ko', MarkerSize=2); hold on
plot(a_tt(2:end), 'r')
plot(a_tt(2:end)+1.96*sqrt(P_tt(2:end)), 'b')
plot(a_tt(2:end)-1.96*sqrt(P_tt(2:end)), 'b')
legend('観測値', 'フィルタ値', '95%区間', box='off', Numcolumns=2)
xlabel('year'); ylabel('Normalized discharge')
ylim([-4, 6])

初期化とパラメータ推定

前節では, カルマンフィルタが無事計算できたものの, パラメータについては先験的にそれっぽい値を与えていた. 本節では, これらを推定する方法を実装する. 推定すべきパラメータは, $\sigma^2_\ve$, $\sigma^2_\eta$, $a_1$, $P_1$ である.

散漫なカルマンフィルタ

初期状態 $a_1$, $P_1$ を決めるに当たり, 何も情報がないと仮定し, $P_1 \rightarrow \infty$ と仮定するのは自然である. その場合, 結果的に

となり, $a_1$, $P_1$ を決める必要がなくなる.

モデルの尤度

最尤推定を行ってパラメータを決めるために, モデルの尤度を求めよう.

初期状態 $a_1$, $P_1$ を与える場合

モデルの対数尤度 $\ell$ は,

で与えられる.

散漫な初期化を行う場合

発散を防ぐことを考慮した以下のような散漫対数尤度 $\ell_d$ が定義される.

実装

散漫なカルマンフィルタの最尤推定を行う. MATLABのOptimaizing Toolboxの, 準ニュートン法（BFGS公式）を用いて, $\sigma^2_\eta$, $\sigma^2_\ve$ に関する散漫な対数尤度を最大化する. ただ, 教科書に書かれている通り, 分散は正数しか取れないので, 以下の変換を行い探索範囲を実数値とできるようにした.

まず, メインのコード.

y = nile;
y = normalize(y);

varEta = 1; % σ^2_η の初期値（適当にきめた）
varEps = 1; % σ^2_ε の初期値（適当にきめた）

psiEta = log(sqrt(varEta)); % ψ_η に変換
psiEps = log(sqrt(varEps)); % ψ_ε に変換

% minimize loglilelihood
options = optimoptions(@fminunc,'Display','iter','Algorithm','quasi-newton'); % 準ニュートン法の設定
x0 = [psiEta, psiEps];              % 探索するパラメータの初期値
f = @(x) -calcLogDiffuseLlhd(y, x); % 最小化したい函数（散漫な対数尤度の最大化なので負号をつける）
xopt = fminunc(f, x0, options);     % 実行

varEtaOpt = exp(2*xopt(1))          % 推定されたψ_ηをσ^2_ηに戻す
varEpsOpt = exp(2*xopt(2))          % 推定されたψ_εをσ^2_εに戻す

以下, メインコードの中で使われた函数.

function logLd = calcLogDiffuseLlhd(y, vars)
% 
% ローカルトレンドモデルの散漫な対数尤度を求める函数.
% y   : データ
% vars: 尤度に関わるパラメータ（ψ_ε, ψ_η）

psiEta = vars(1); varEta = exp(2*psiEta); % σ^2_η に戻す
psiEps = vars(2); varEps = exp(2*psiEps); % σ^2_ε に戻す
L = length(y);

% a_1, P_1の初期値 式（dissufe init.）参照のこと
a1 = y(1); 
P1 = varEps;

% カルマンフィルタリング
[~, ~, F_t, v_t] = localTrendKF(y, a1, P1, varEta, varEps); 

% 散漫対数尤度を計算
tmp = sum(log(F_t(2:end)) + v_t(2:end).^2 ./ F_t(2:end));
logLd = -0.5*L*log(2*pi) - 0.5 * tmp;

end

function [a_tt, P_tt, F_t, v_t] = localTrendKF(y, a1, P1, varEta, varEps)
%
% ローカルトレンドモデルのカルマンフィルタリングを行う函数

L = length(y);

% Preallocation
a_tt1 = zeros(size(y)); a_tt1(1) = a1;
P_tt1 = zeros(size(y)); P_tt1(1) = P1;
v_t   = zeros(size(y)); 
F_t   = zeros(size(y)); 
a_tt  = zeros(size(y)); 
P_tt  = zeros(size(y));
K_t   = zeros(size(y));

% Filtering
for t = 1:L
    
    % Innovation
    v_t(t) = y(t) - a_tt1(t);
    F_t(t) = P_tt1(t) + varEps;
    
    % Kalman gain
    K_t(t) = P_tt1(t)/F_t(t);

    % Current state
    a_tt(t) = a_tt1(t) + K_t(t)*v_t(t);
    P_tt(t) = P_tt1(t) * (1 - K_t(t));

    % Next state
    a_tt1(t+1) = a_tt(t);
    P_tt1(t+1) = P_tt(t) + varEta;
    
end
end

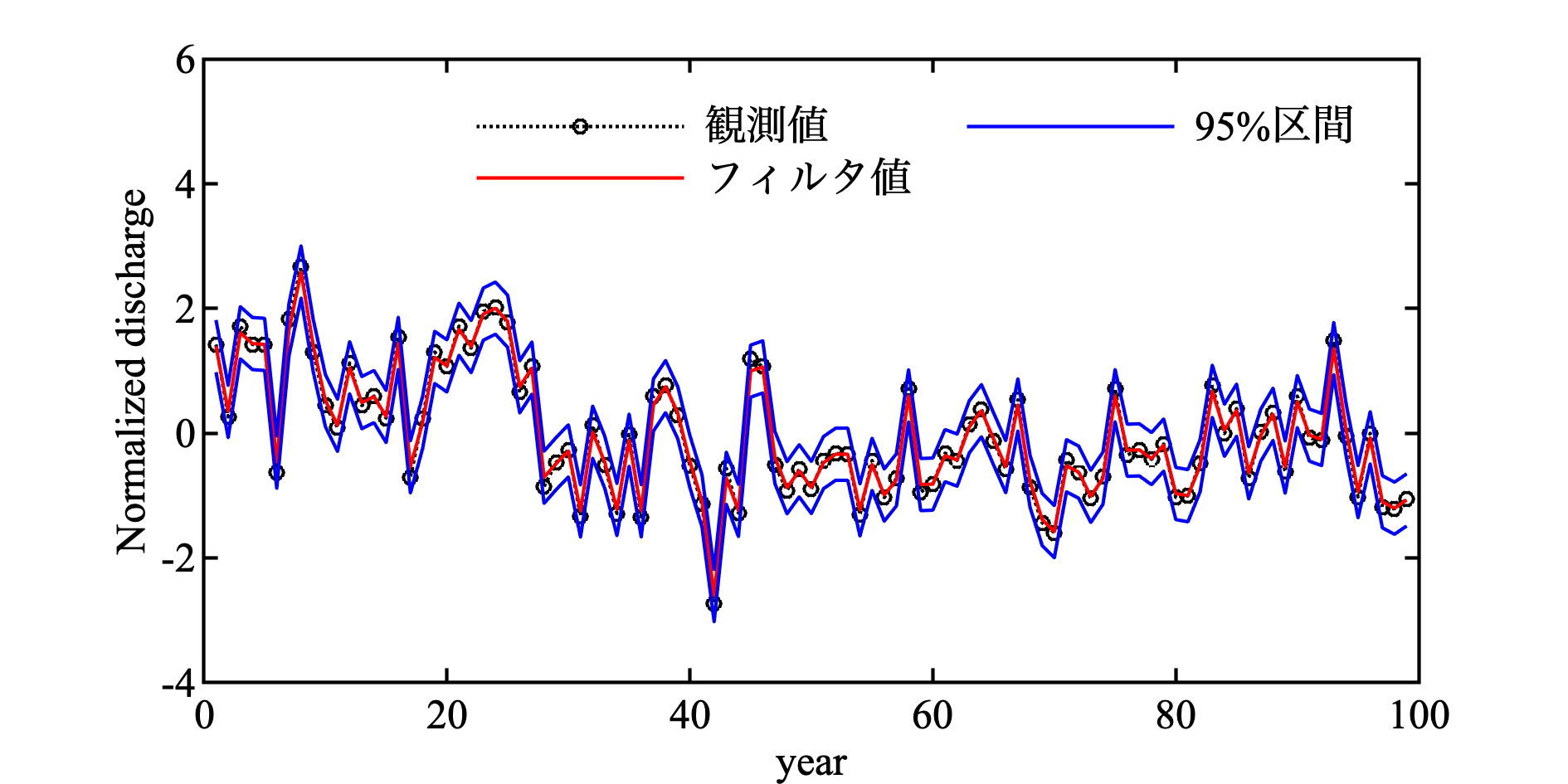
計算結果, $\sigma^2_\eta = 0.0494$, $\sigma^2_\ve = 0.5307$ となった. これらを, パラメータとしたカルマンフィルタを行い, 結果を見てみる.

varEps = varEtaOpt;
varEta = varEpsOpt;

a1 = varEps;
P1 = varEta;

[a_tt, P_tt, ~, ~] = localTrendKF(y, a1, P1, varEta, varEps);

plot(y(2:end), ':ko', MarkerSize=2); hold on
plot(a_tt(2:end), 'r')
plot(a_tt(2:end)+1.96*sqrt(P_tt(2:end)), 'b')
plot(a_tt(2:end)-1.96*sqrt(P_tt(2:end)), 'b')
legend('観測値', 'フィルタ値', '95%区間', box='off', Numcolumns=2)
xlabel('year'); ylabel('Normalized discharge')
ylim([-4, 6])

どうもきれいすぎる（フィルタリングがデータを追いすぎている）気がする. じきに, 再確認します.