『ゼロからできるMCMC』 Chapter6 Metropolis HastingsをJuliaで
最終更新:2020/11/27
『ゼロからできるMCMC』 Chapter6 Metropolis Hastingsのコードを, 練習を兼ねてJuliaで書いてみました. 詳細なことを書くと著作権的にだめな気もするので, 解説などはありません.
Julia Version 1.5.0
作用を定義
Metropolis法とMetropolis Hastings法を用いて以下の作用で定義される函数から サンプリングする. 教科書p.130で提案されている作用なので, 詳しくは教科書を見てもらいたい.
\begin{align}
S(x) = \frac{1}{2}x^2 + \frac{1}{4}x^4
\end{align}
Metropolis法
まずは, Metropolis法. chapter4 で作った函数を流用.
Julia
using Plots
using Random:seed!
using Distributions
## メトロポリス
action(x) = 0.5*x^2 + 0.25*x^4 # 作用の定義
function metropolis1d(;niter=10^5)
seed!(12345)
step_size = 0.5
# initial values
x = 0.0
naccept = 0
xs = zeros(niter)
# main
for i = 1:niter
backup_x = x
action_init = action(x)
x += (rand()-0.5)*step_size*2.0 # xの更新
action_fin = action(x)
# Metropolis test
metropolis = rand()
exp(action_init - action_fin) > metropolis ? naccept+= 1 : x=backup_x
xs[i] = x
end
acceptrate = naccept/niter # 受理確率
return xs, acceptrate
end
# 結果
xs, r = metropolis1d()
pyplot(fmt=:svg, size=(400, 300))
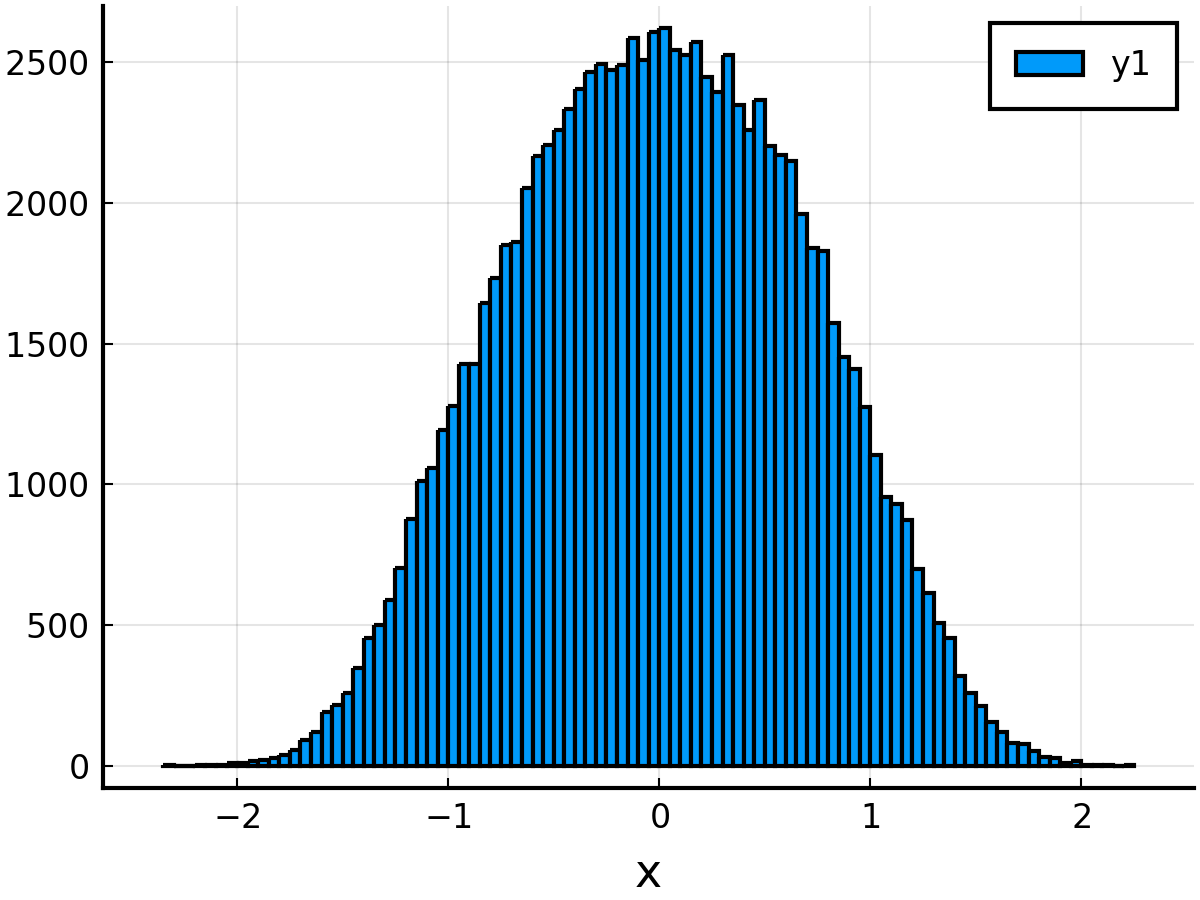
histogram(xs)
xlabel!("x")
PyPlot.savefig("MH_m.png", dpi=300)
結果. 受理確率rは0.37674でした.
Metropolis Hastings法
Julia
actionMH(x) = 0.25*x^4 # 作用の定義(作用と呼んでいいのか怪しいが)
function MH1d(;niter=10^5)
seed!(12345)
# initial values
x = 0.0
naccept = 0
xs = zeros(niter)
# main
for i = 1:niter
backup_x = x
action_init = actionMH(x)
x = randn() # xの更新 ( 正規分布からのサンプル )
action_fin = actionMH(x)
# Metropolis test
metropolis = rand()
exp(action_init - action_fin) > metropolis ? naccept+= 1 : x=backup_x
xs[i] = x
end
acceptrate = naccept/niter # 受理確率
return xs, acceptrate
end
# 結果
xsMH, rMH = MH1d()
pyplot(fmt=:svg, size=(400, 300))
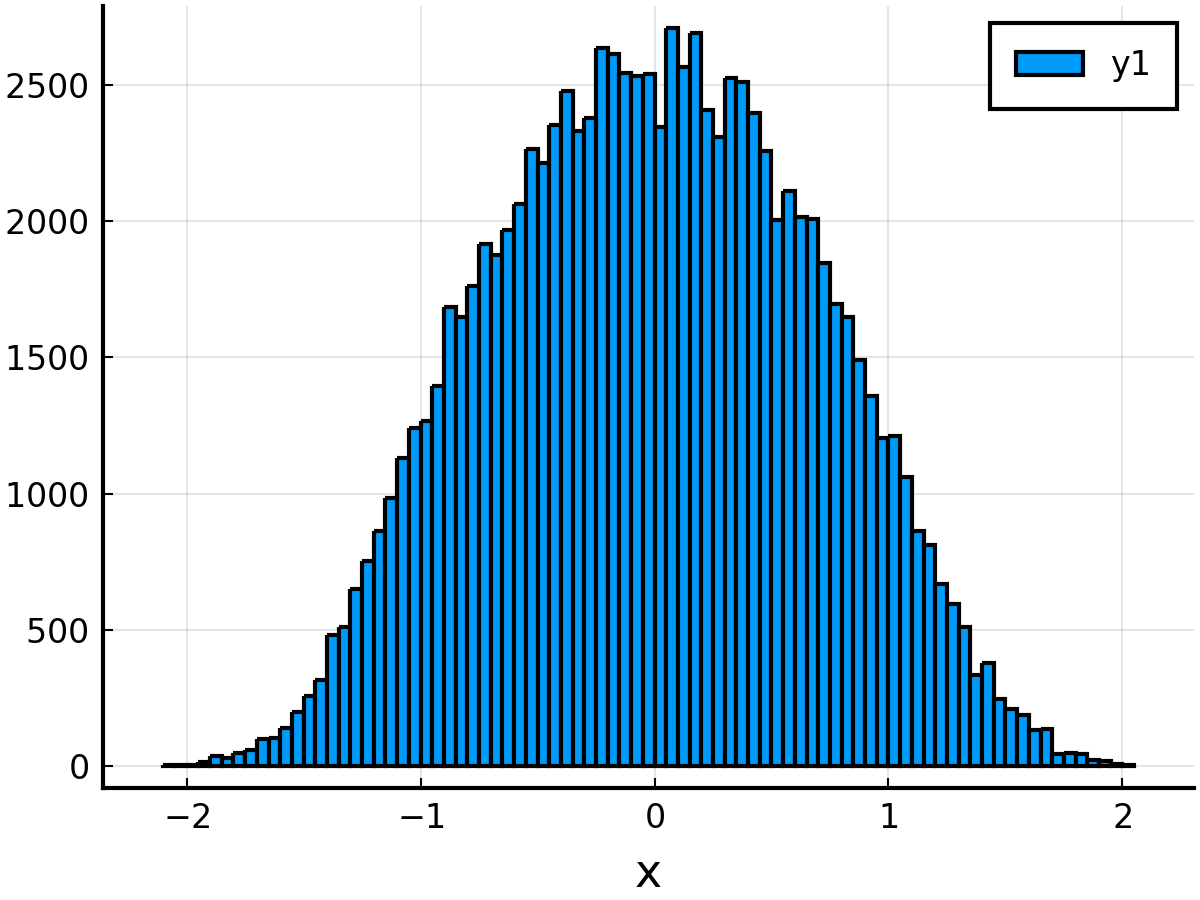
histogram(xsMH)
xlabel!("x")
PyPlot.savefig("MH_mh.png", dpi=300)
結果. 受理確率rMHは0.79837.
メトロポリス法と比べて, 受理確率が二倍程度になった.