第2回 MATLAB seminar 2022年10月05日

最終更新：2022/10/13

今年は, まず図を作る方法から学ぼうと思う. せっかくなので, データもどこかから取ってくるのではなくて自分で作ることで計算方法を学ぶ. 公式サイトから自分のほしい図を選ぼう.

いろいろな図

plot

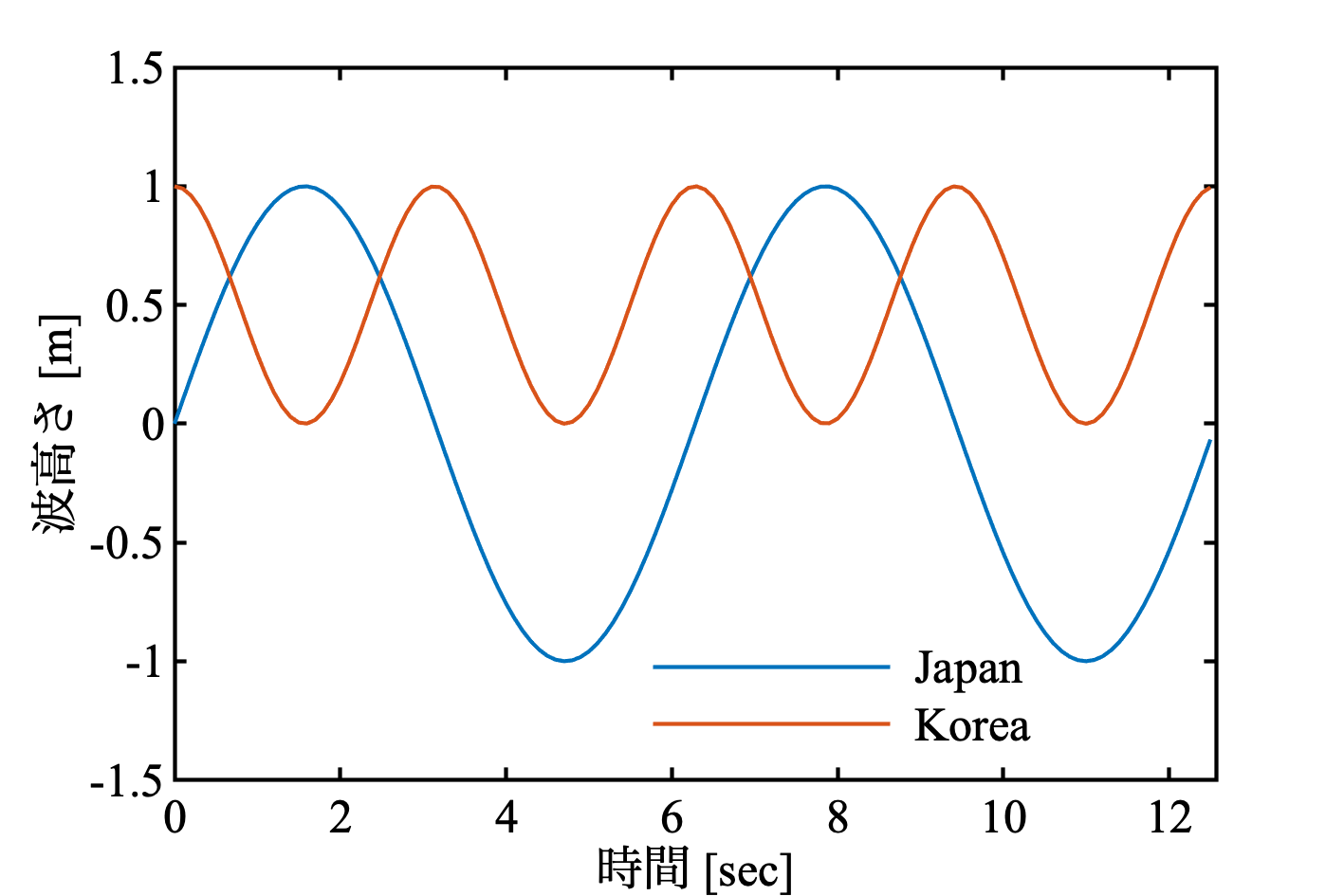
まずは僕が最もよく使う plot 関数.

図1

name
MATLAB 
x = 0:0.1:4*pi;
y = sin(x);
plot(x, y)

% ラベル
xlabel('時間 [sec]')
ylabel('波高さ [m]')

% 2つ以上図を重ねるならholdする. 
hold on

y2 = cos(x).^2;
plot(x, y2)

% x軸をy軸の範囲を指定する.
ylim([-1.5, 1.5])
xlim([0, 4*pi])

% 凡例をいれる(僕は凡例につく箱が嫌いなのでBox='off'で箱なしにしている).
legend('Japan', 'Korea', Box='off')

stem, histogram

データ特性を見るときに役立つ stem, histogram. 身長を想定して, 平均170, 標準偏差10のデータを100個(100人分)作る.

図2

name

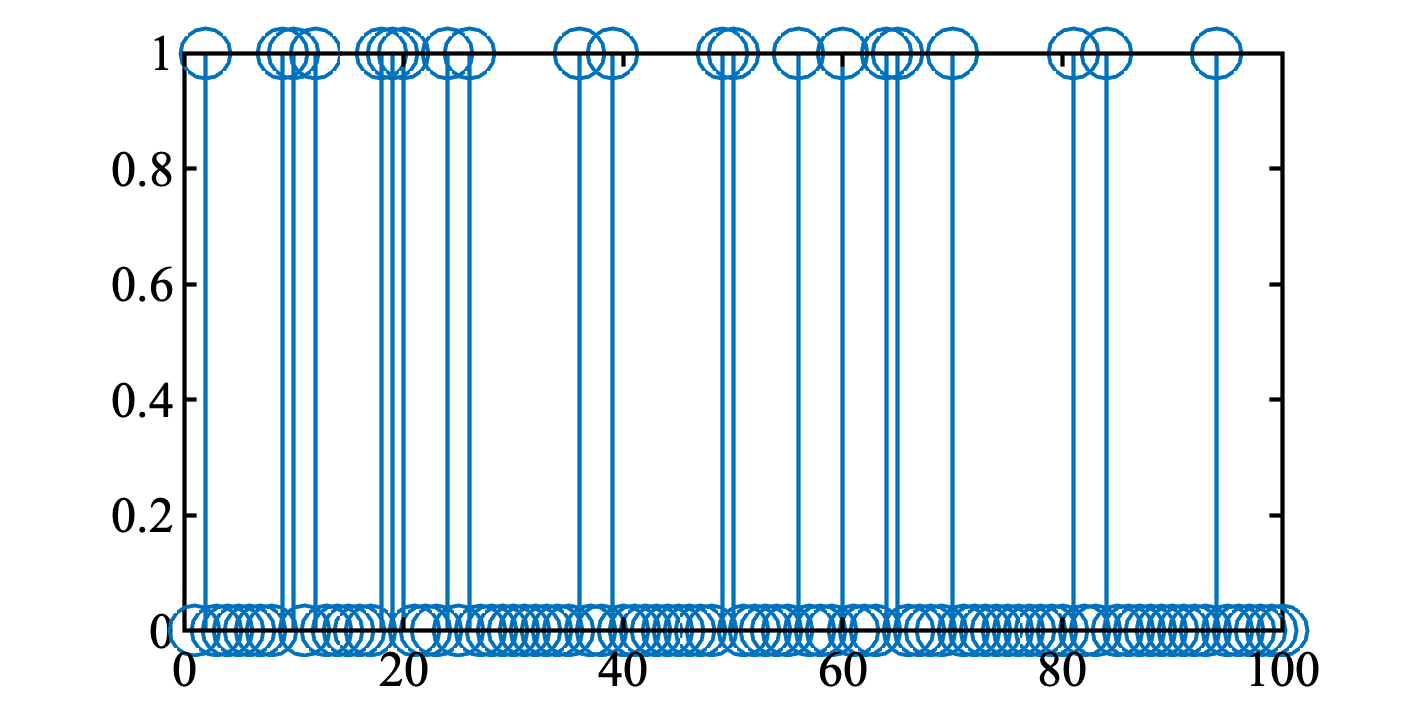
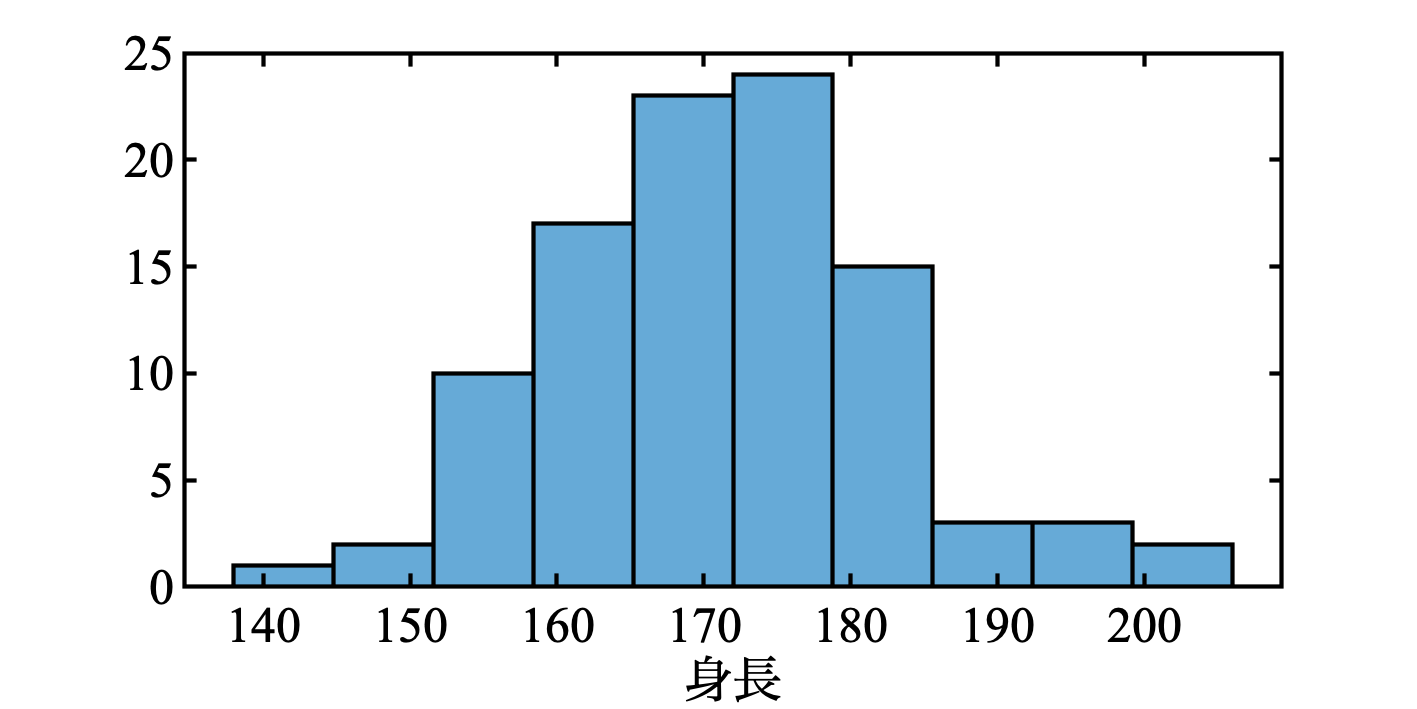
図3

name
MATLAB 
heikin = 170;
hensa  = 10;
shincho = heikin + randn(100, 1)*hensa;

% 色々プロットしてみる
% stem(shincho)
stem(shincho>180) % 180以上のデータの在り処をみる(図2)
% histogram(shincho) % ビンの数を自動的に決めてもらうならこれを使う
histogram(shincho, 'NumBins', 10) % (図3)

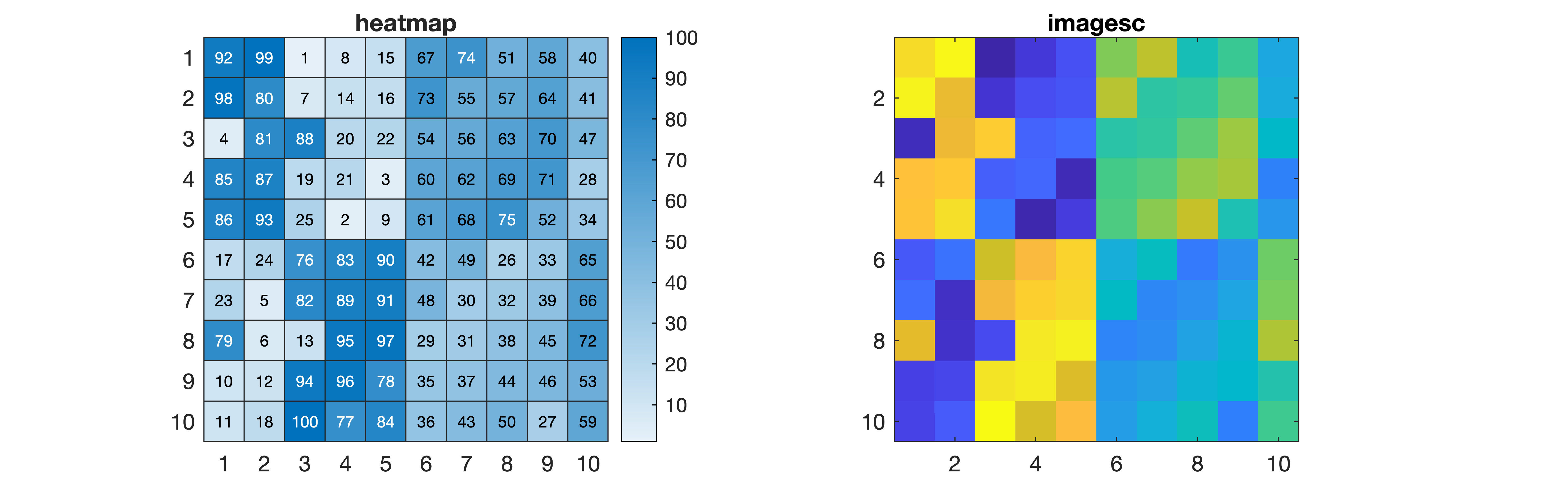
heatmap, imagesc

2次元のデータを見るときに役立つ heatmap, imagesc. magic という魔法陣を作る関数を使って二次元データを作り, 可視化.

name
MATLAB 
A = magic(10);
heatmap(A) % (図heatmap)
imagesc(A) % (図imagesc)

bar

よくスライドとかで使われる棒グラフを作る bar 関数. fibo というフィボナッチ数列を作る関数を自作し, 可視化. N を変えて, フィボナッチ数列が爆発的に増加することを確認しよう. logをとっても面白いかもしれない.

name
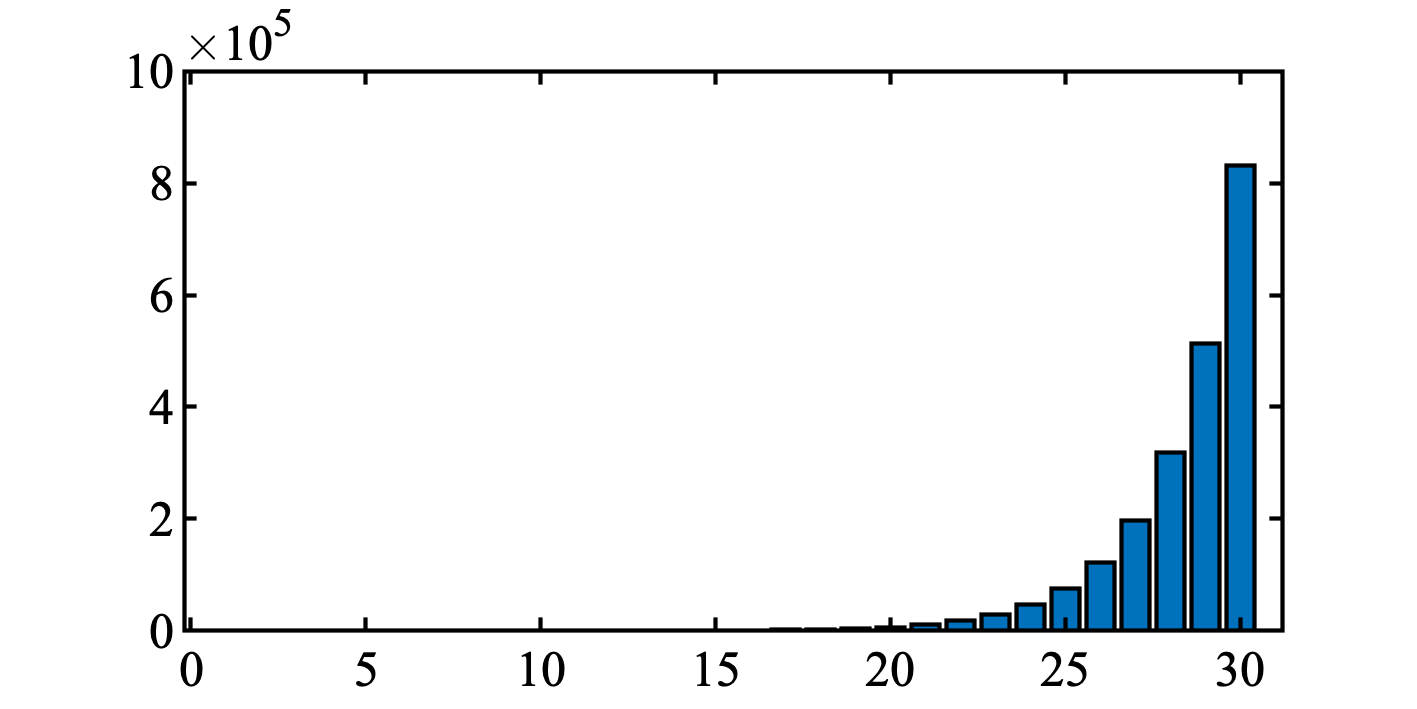
MATLAB 
N = 30;
F = fibo(N);
bar(F)

% フィボナッチ数列を作る関数(関数は一つのファイルの一番下か, 別ファイルとしないといけないので注意).
function out = fibo(N)
    out = zeros(N, 1);
    out(1) = 1;
    out(2) = 1;
    for I = 3:N
        out(I) = out(I-1) + out(I-2);
    end
end

三次元プロット

目で見て楽しい三次元プロットを作ろう. 2変数関数を可視化する. キーとなるのは meshgrid 関数.

\begin{align} f(x, y) = \cos(x)\sin(y) \end{align}
name
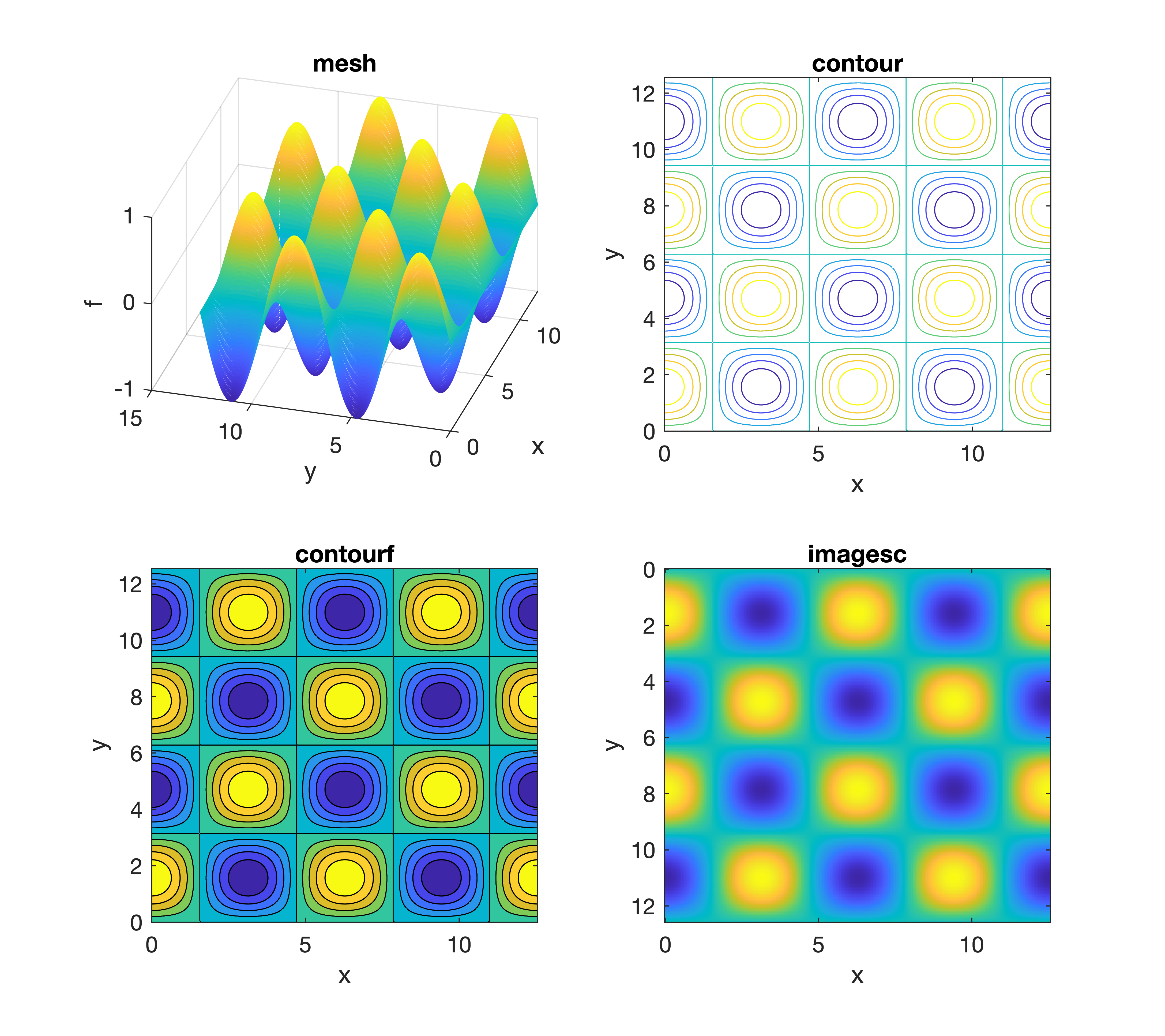
MATLAB 
x = 0:0.05:4*pi;
y = 0:0.05:4*pi;
[x_grid, y_grid] = meshgrid(x, y);

z = cos(x_grid) .* sin(y_grid);
mesh(x, y, z)
surf(x, y, z)
contour(x, y, z)
contourf(x, y, z)
imagesc(x, y, z)

% https://jp.mathworks.com/help/matlab/ref/colormap.html を みて,
% 色々変えてみてください.
colormap parula
colorbar

xlabel('x'); ylabel('y'); zlabel('f')

点プロット

点プロットを作ろう. データは, 決定論的な値に乱数を足すことで作る.

name
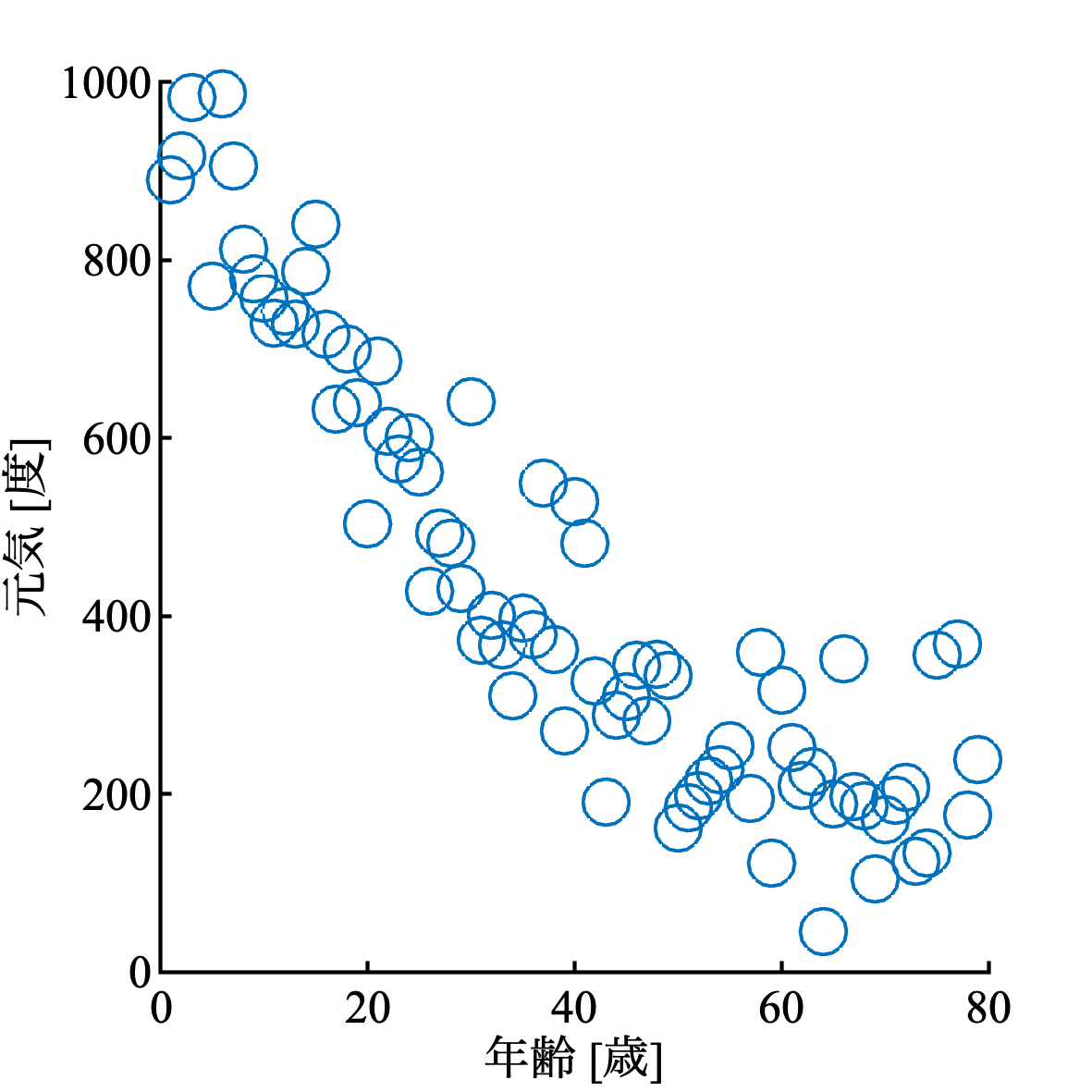
MATLAB 
x      = (0:1:80)';
y_true = 1000*exp(-x/40);
L = length(x);
scatter(x, y_true)
ylim([0, 1000])

r = 100*randn(L, 1);
y = y_true + r;
scatter(x, y)
ylim([0, 1000])
xlabel('年齢 [歳]')
ylabel('元気 [度]')

この記事のTOP    BACK    TOP