第8回 MATLAB seminar 2021年07月26日

最終更新：2021/07/26

今日は, 常微分方程式を簡単に差分法で解いた. 特に, Lotka-Volterra方程式とLorenz Attractorは, 見た目の不思議さに加え面白い背景があるので, 興味があれば各自調べてみてほしい.

1変数：空気抵抗のある自由落下

モデル

\begin{align}\large{ m \frac{dv}{dt} = mg - k v \notag }\end{align}

これは, みなわかるでしょう. $k$ は空気抵抗係数.

初速度0で落とした場合, 理論値は以下となる. せっかくなので, 理論値も計算してプロットしている.

\begin{align}\large{ v(t) = \frac{mg}{k} \left( 1 - \exp{ \left( -\frac{k}{m}t \right)} \right). }\end{align}

離散化

以下のように離散化する.

\begin{align}\large{ \frac{v_{i+1} - v_{i}}{\Delta t} = g - \frac{k}{m} v_i \\ }\end{align}
結局は以下の式を解けばいい. $\Delta t$ は時間の刻み幅, あまり大きいと計算がうまくいかない.
\begin{align}\large{ v_{i+1} = v_{i} + \Delta t \left( g - \frac{k}{m} v_i \right) }\end{align}

シミュレーション

MATLAB 
% INPUTS
dt     = 0.1;   % 時間刻み [sec]
T      = 10;    % 計算時間 [sec] 
g      = 9.81;  % 重力加速後 [m*s^(-2)]
m      = 0.3;   % 質量 [kg]
k      = 0.24;  % 空気抵抗係数 [kg/m]
v_init = 0;     % 速度の初期値

% 計算
t = 0:dt:T;         % 計算範囲 ( 時間 ) 
v = zeros(size(t)); % 事前割り当て 
L = length(t);
v(1) = v_init;

for I = 1:L-1
   v(I+1) = v(I) + dt * (g - (k/m) * v(I));
end

% 理論値
v_true = zeros(size(t)); 
for I = 1:L 
   v_true(I) = (m*g/k)*(1 - exp(-k*t(I)/m)); 
end

% OUTOUT (plot)
plot(t, v);      hold on    % 計算値
plot(t, v_true); hold off   % 理論値
legend('計算値', '理論値')

xlabel('Time [sec]')
ylabel('Velocity [m/s]')
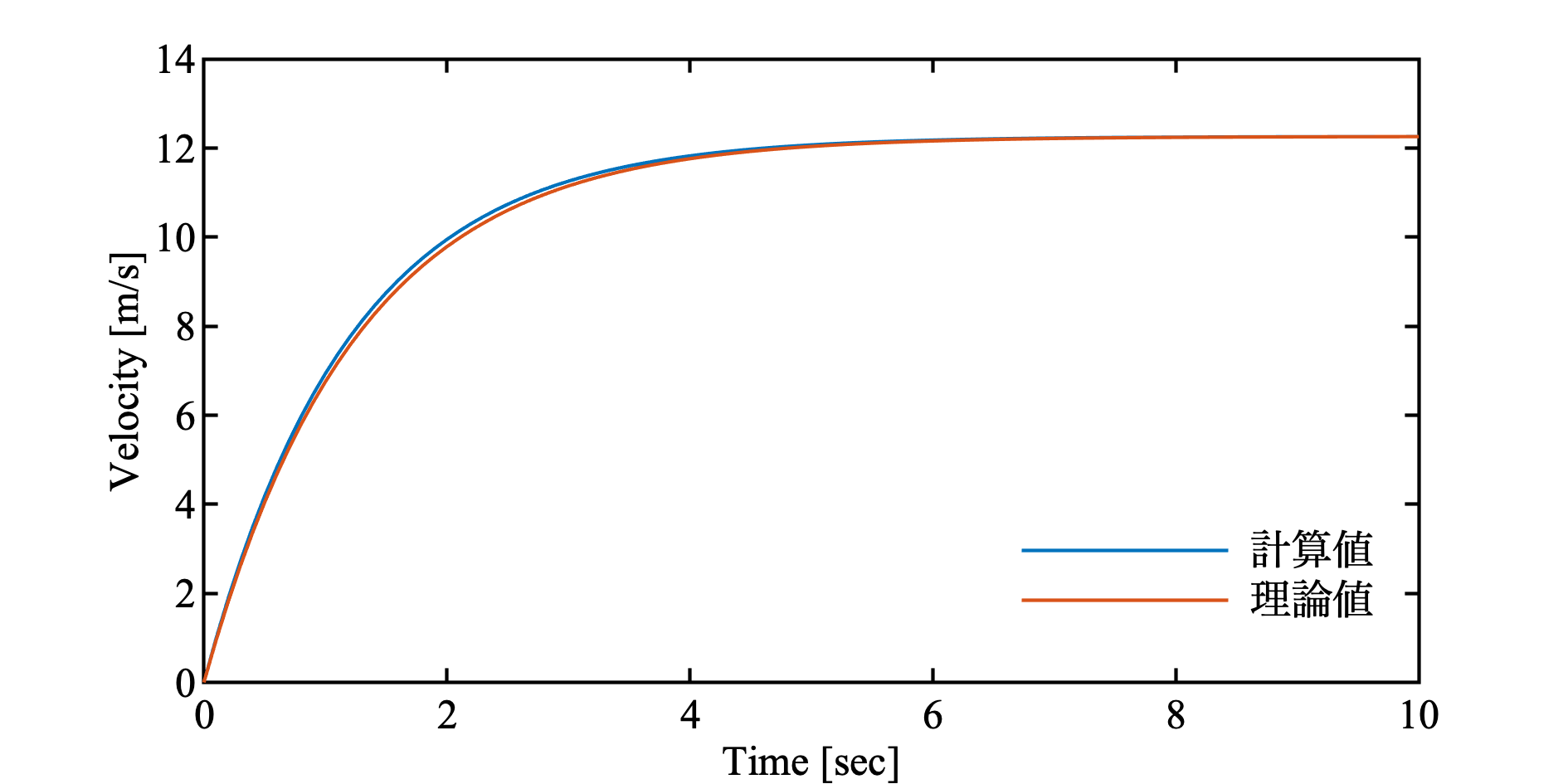
result

計算値の精度を少し落とすために時間刻みを少し大きめ ( $\Delta t = 0.1$ ) にとった.

2変数：Lotka-Volterra方程式

モデル

$x$ ：被食者の個体数と $y$ ：捕食者の個体数との関係が, 以下の4つのパラメータをもつ方程式で表されるときの, それぞれの個体数の時間発展を計算する. 詳しいことは, ロトカ・ヴォルテラの方程式 ( wikipedia ) など.

\begin{aligned} & \large{\frac{d x}{d t}=a x-b x y} \\ & \large{\frac{d y}{d t}=c x y-d y} \end{aligned}

離散化

以下のように離散化する.

\begin{align}\large{ \frac{x_{i+1} - x_{i}}{\Delta t} = a \, x_i - b \, x_i \, y_i, \\ \frac{y_{i+1} - y_{i}}{\Delta t} = c \, x_i \, y_i - d \, y_i. }\end{align}
結局以下の式を解けば良い.
\begin{align}\large{ x_{i+1} = x_{i} + \Delta t \left( a \, x_i - b \, x_i \, y_i \right), \\ y_{i+1} = y_{i} + \Delta t \left( c \, x_i \, y_i - d \, y_i \right). }\end{align}

シミュレーション

MATLAB 
% INPUT
dt = 0.002; 
T = 30;
a = 2.0;
b = 0.3;
c = 0.2;
d = 1.0;
x_init = 10;
y_init = 5;

% calc
t = 0:dt:T;
x = zeros(size(t)); x(1) = x_init;
y = zeros(size(t)); y(1) = y_init;
L = length(t);

for I = 1:L-1
    x(I+1) = x(I) + dt * (a * x(I) - b*x(I)*y(I));
    y(I+1) = y(I) + dt * (-d*y(I) + c*x(I)*y(I));
end

% OUTPUT
plot(t, x); hold on
plot(t, y); hold off

xlabel('時間')
ylabel('個体数')
l = legend('被食者', '捕食者', 'Box', 'off');
l.Orientation = 'horizontal';
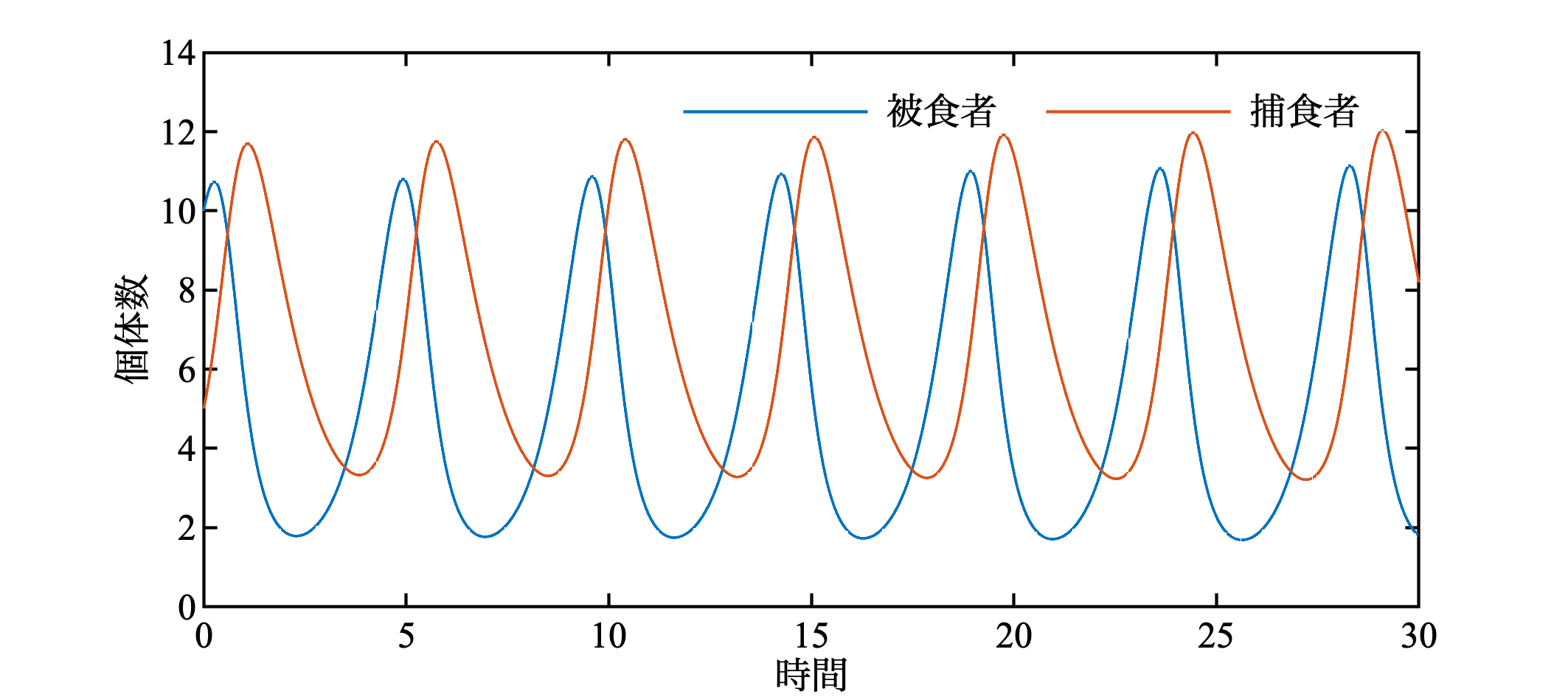
result

被食者が増えると, 捕食者が増え, 捕食者が増えると, 被食者が減るという関係が現れている. 是非, パラメータの意味を調べて, 色々パラメータを変えてみてほしい.

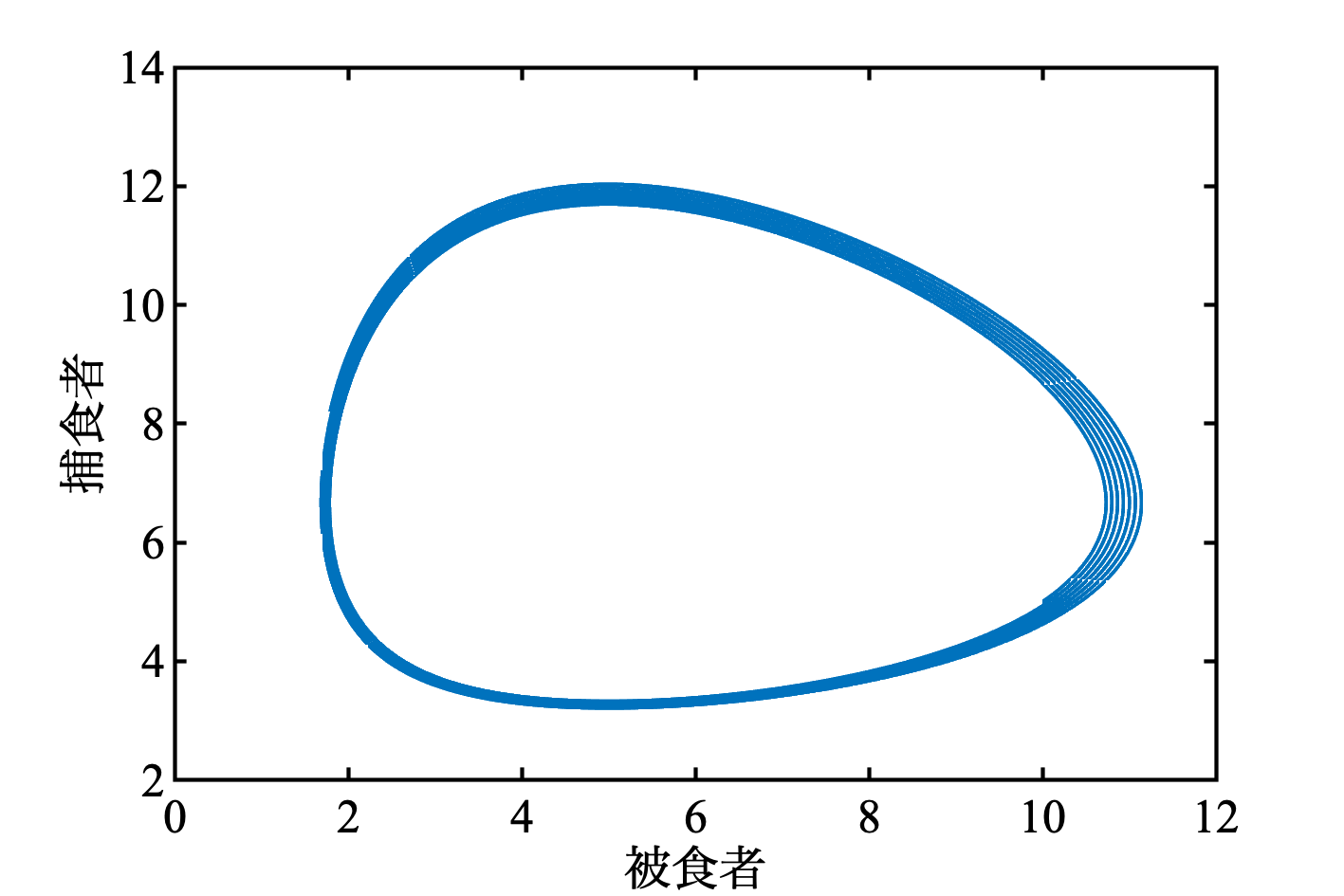
ちなみに, 被食者と捕食者の関係をプロットすると ( 一周する ) 閉曲線となることが理論的に知られている. しかし, このシミュレーションでは, 微妙に閉じていない. これは, 計算精度の問題である ( このモデルには保存量があるが, 離散的に計算する過程で減少し保存されていない ) . $\Delta t$ を色々変えて, このプロットがどうなるか見てみてほしい.

result
MATLABコード MATLAB 
plot(x, y)
xlabel('被食者')
ylabel('捕食者')

3変数：Lorenz Attractor

モデル

変数は, $x$, $y$, $z$ の3つ, パラメータも3つである. 詳しいことは, ローレンツ方程式 ( wikipedia ) など.

\begin{align}\large{ \frac{d x}{d t}=-p x+p y \\ \frac{d y}{d t}=-x z+r x-y \\ \frac{d z}{d t}=x y-b z }\end{align}

パラメータを $p = 10$, $r = 28$, $b = 8/3$ と設定したときの挙動が有名である.

離散化

以下のように離散化する.

\begin{align}\large{ \frac{x_{i+1} - x_{i}}{\Delta t} = -p x_i+p y_i \\ \frac{y_{i+1} - y_{i}}{\Delta t} = -x_i z_i+r x_i-y_i, \\ \frac{z_{i+1} - z_{i}}{\Delta t} = -x_i y_i - b z_i. }\end{align}
結局以下の式を解けば良い.
\begin{align}\large{ x_{i+1} = x_{i} + \Delta t \left(-p x_i+p y_i \right)\\ y_{i+1} = y_{i} + \Delta t \left(-x_i z_i+r x_i-y_i\right), \\ z_{i+1} = z_{i} + \Delta t \left(-x_i y_i - b z_i\right). }\end{align}

シミュレーション

MATLAB 
% INPUT
dt = 0.002;
T  = 30;
r = 28;
s = 10;
b = 8/3;
x_init = 1;
y_init = 1;
z_init = 1;

% calc

t = 0:dt:T;
x = zeros(size(t)); x(1) = x_init;
y = zeros(size(t)); y(1) = y_init;
z = zeros(size(t)); z(1) = z_init;
L = length(t);


for I = 1:L-1
    x(I+1) = x(I) + dt*(s*(y(I) - x(I)));
    y(I+1) = y(I) + dt*(x(I)*(r - z(I)) - y(I));
    z(I+1) = z(I) + dt*(x(I)*y(I) - b*z(I));       
end

plot3(x, y, z)
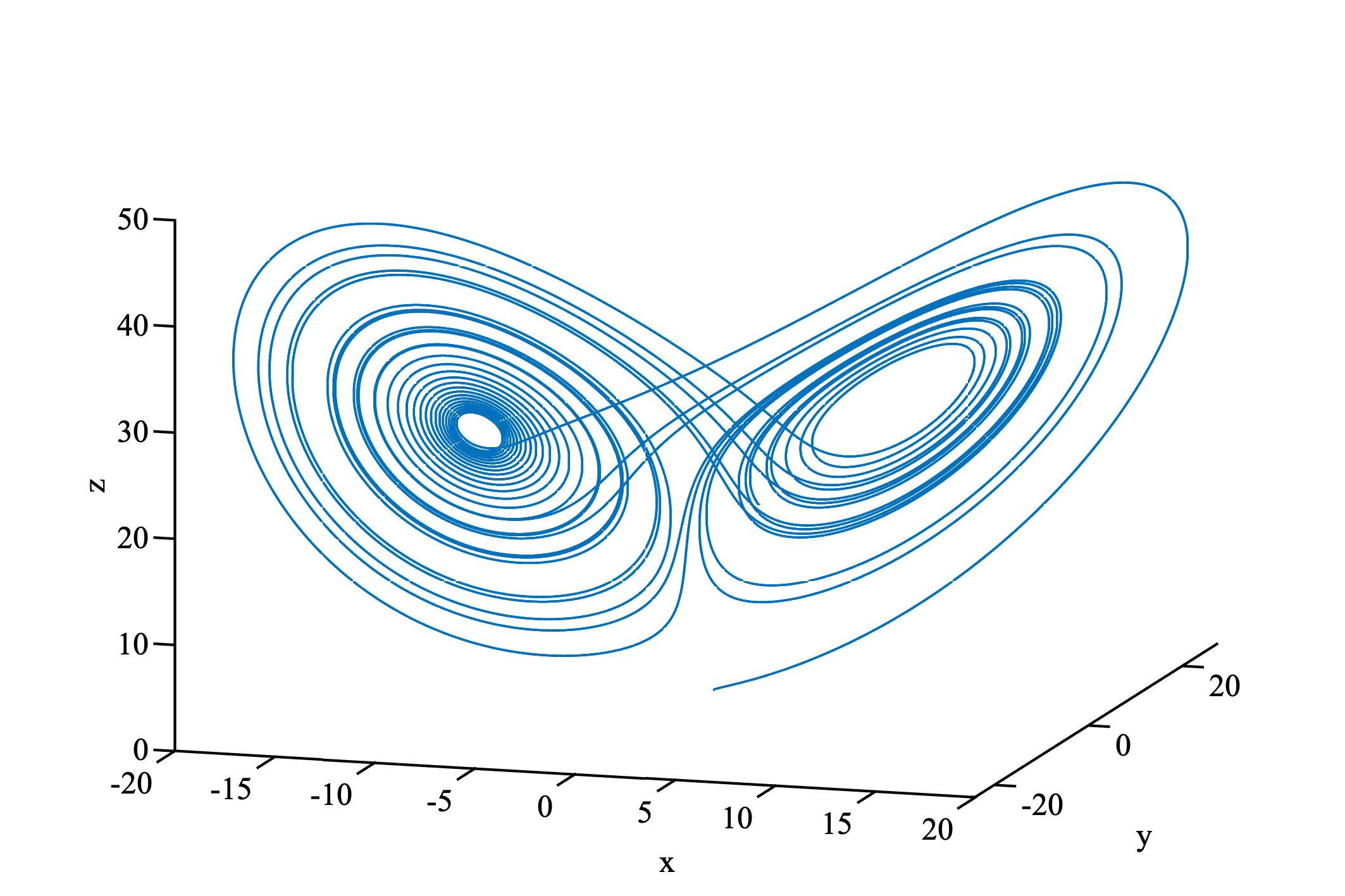
result

カオス的なふるまいをする. 初期値鋭敏性をもっており, ほんの少しでも初期値を変えると途中から全然異なる動きをする. それが, 気象の予想の難しさなどと関係がある. 興味がある人は調べてみてほしい.

なお, 以下のコードを使うとアニメーションとしてみることができる.

MATLAB 
plot3(x, y, z)
yl = ylim;
xl = xlim;
zl = zlim;

figure;
int = 50;
h = animatedline;
axis([xl yl zl])
temp = int - 1;

pause(3)
for k = 1:int:length(t)-temp
    xvec = x(k:k+temp);
    yvec = y(k:k+temp);
    zvec = z(k:k+temp);
    addpoints(h, xvec, yvec, zvec);
    drawnow 
end

参考文献

数理モデルに興味があれば, 以下の本がおすすめ. 微分方程式で数学モデルを作ろう

この記事のTOP    BACK    TOP