第7回 MATLAB seminar 2021年07月20日

最終更新：2021/07/26

乱数の勉強.

乱数を作ってみる

MATLABで作れる基本的な乱数をいくつか作ってみた.

$[0, 1]$ の一様分布

MATLAB 
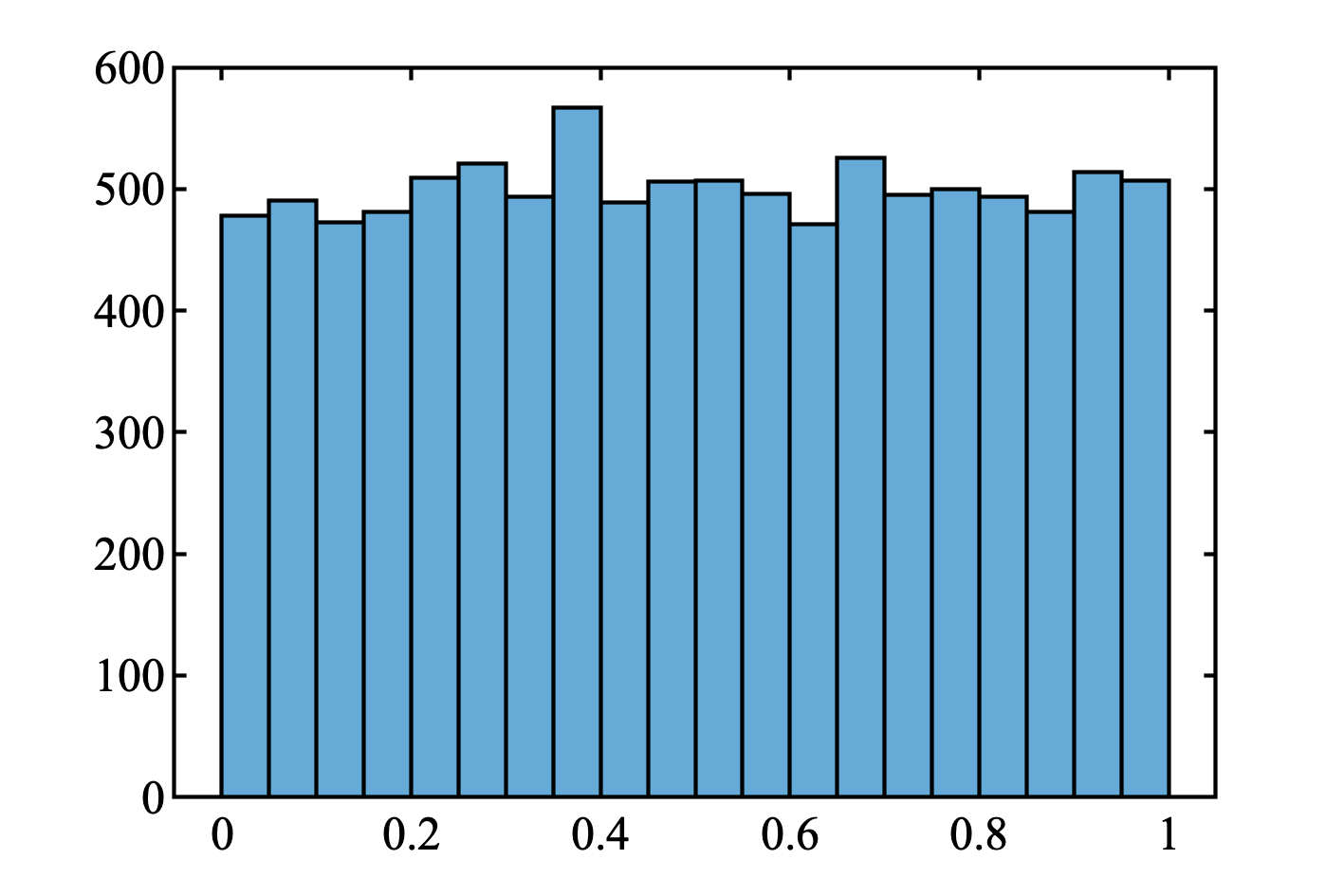
% 一つ作ってみる
>> rand()
ans = 0.1415

% 10000個作って分布をみてみる. 
r = rand([10000 1]);
histogram(r)

一様分布っぽいのでOK.

result

平均 $0$ 分散 $1$ の正規分布

MATLAB 
% 一つ作ってみる
>> randn()
ans = 0.0460

% 10000個作って分布をみてみる. 
r = randn([10000 1]);
histogram(r)
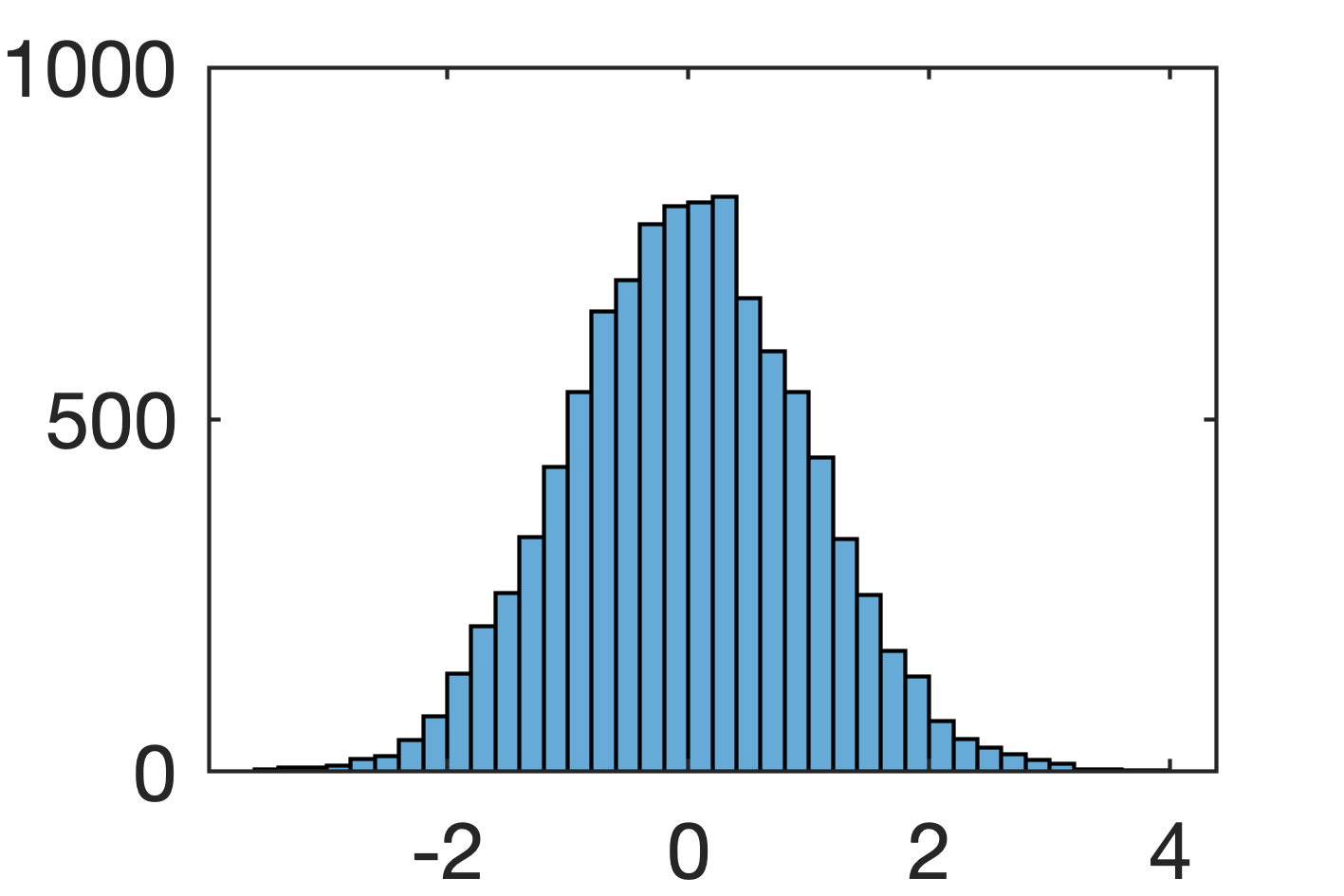
result

正規分布っぽいのでOK. 僕は, ( というか一般的に ) 平均 $\mu$, 分散 $\sigma^2$ の正規分布をしばしば, $\mathcal{N}(\mu, \sigma^2)$ と書き, 変数 $r$ がこの分布にしたがってサンプルされていることを,

\begin{align}\large{ r \sim \mathcal{N}(\mu, \sigma^2) \notag }\end{align}
とかく.

上のコードでのサンプルは, $r \sim \mathcal{N}(0, 1)$ である. もし, $\mathcal{N}(\mu, \sigma^2)$ からサンプルしたければ, $r * \sigma + \mu$ などすればよい.

整数からの乱数

整数からサンプルを取る場合は, 範囲を指定しなければならない. 以下は, $3 \sim 10$ の範囲から５つサンプルする例.

MATLAB 
>> randi([3 10], [1 5])

ans =
8     7     5     7    10

乱数のシード

乱数を発生させる前にシードをrngで発生させることにより, 同じ乱数を発生させることができる.

MATLAB 
% try 1
rng(12345)
rand(2) % 整数nを一つ渡すとn×n行列の乱数を返す. 

ans =
0.9296    0.1839
0.3164    0.2046

% try 2
rng(12345)
rand(2)

ans =
0.9296    0.1839
0.3164    0.2046

% seedをシャッフル
rng('shuffle')
rand(2)

ans =
0.2173    0.6851
0.0079    0.9720

簡単な検定

日本で, 夫婦が完全にランダムに相手を選ぶと仮定すると, どれくらいの確率で夫の身長＜妻の身長となるかシミュレーションしてみる.

MATLAB 
% 基本情報
muXX = 167.6;  % 20以上の男性の平均身長
muXY = 154.1;  % 20以上の女性の平均身長
stdXX = 5.8;   % 20以上の男性の身長の標準偏差
stdXY = 5.4;   % 20以上の女性の身長の標準偏差

% 3000 夫婦のデータを作る. 
N = 3000;
rng(12345) % seed 
XXs = randn([N, 1])*stdXX + muXX;
XYs = randn([N, 1])*stdXY + muXY;

% 一応ヒストグラムをみてみる
histogram(XXs); hold on
histogram(XYs); hold off
legend('男', '女')
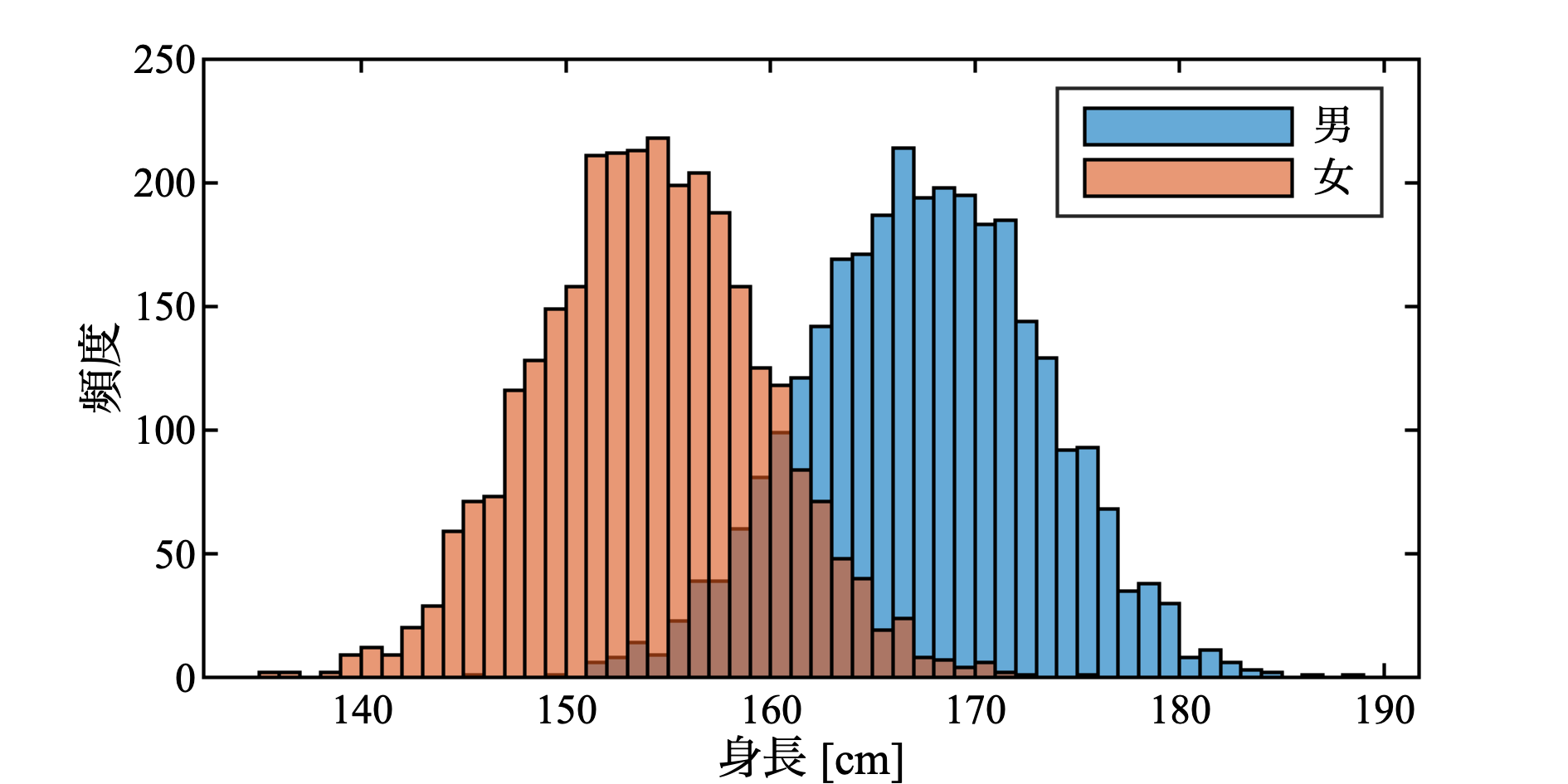
result

結構それらしいヒストグラム. まあ, 平均身長などは本当の統計データを使っているので当然か.

女性の身長の方が大きいペアを数え, 割合をだす.

MATLAB 
>> 100*sum(XXs < XYs)/N

ans =
4.7667

4.7%くらいになった. 男女が全く身長を考慮に入れずに結婚しているなら２０組に１組くらいは女性の方が身長が大きい夫婦が生じるはずである.

もちろん, この解析はガバガバなので結果を真実だと真に受けないように.

線形回帰モデルからのシミュレーション

線形回帰を行った後, もう一歩進んだ見方をすることで理解を深める.

データを見てみる

以下のようなデータに線形回帰を適用する. これは, 僕が作った人工データだけど, まあ小型動物の体長と走る速さの関係などと思ってくれたらいい.

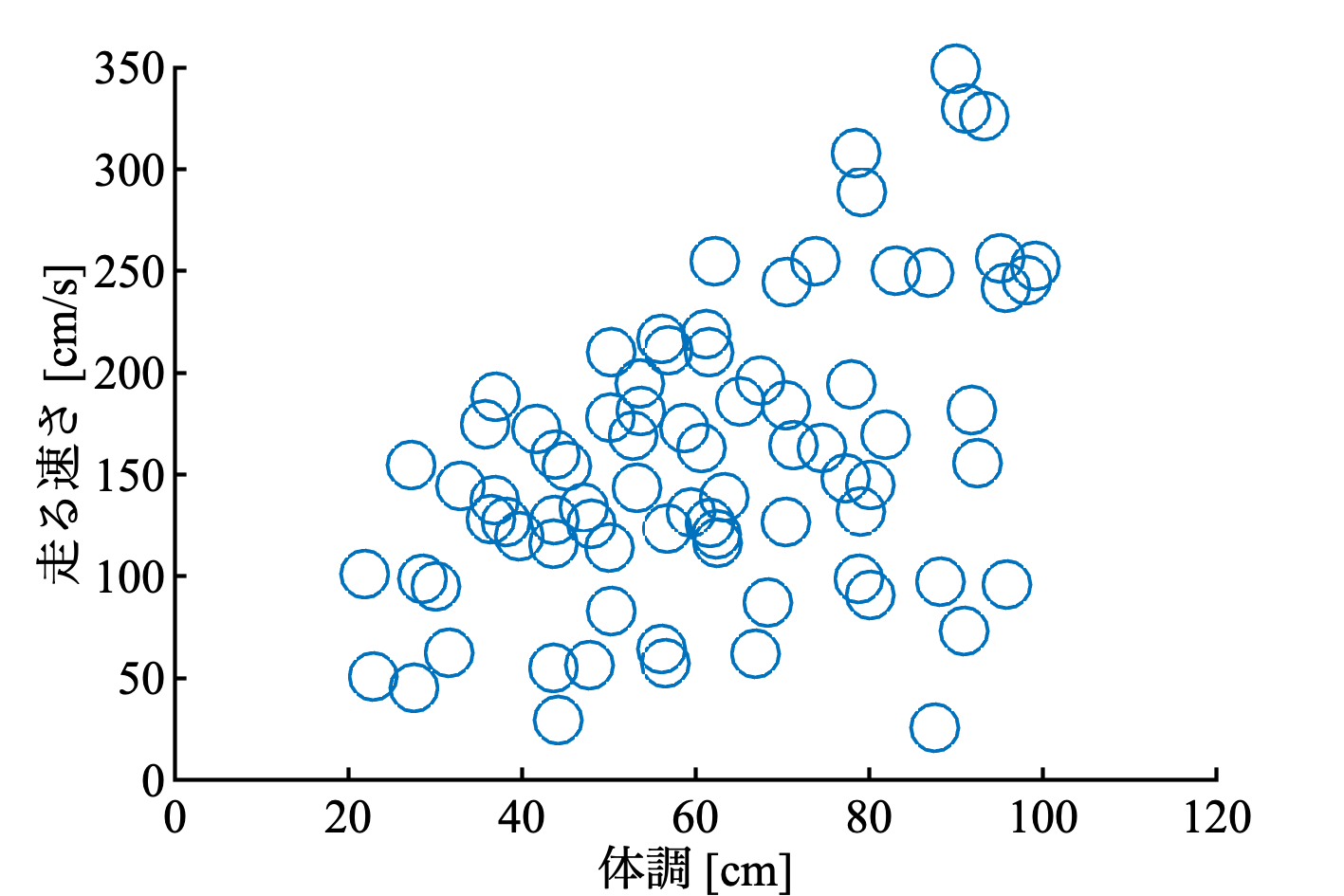
result
図を描くMATLABコード MATLAB 
scatter(x, y)
xlim([0 120])
ylim([0 350])
xlabel('体調 [cm]')
ylabel('走る速さ [cm/s]')

線形回帰を行う

以下の形の線形回帰の係数を求める. 係数の求め方は, 第二回参照.

\begin{align}\large{ y = b(1) + b(2)x. \notag }\end{align}

MATLAB 
X = [ones(L,1) x];
% 以下, どちらでもいい. 
b = X\y; 
b = inv(X'*X)*X'*y; 

% 可視化
scatter(x, y); hold on
xfit = (15:105)';
yfit = b(1) + b(2)*xfit;
plot(xfit, yfit)
xlim([0 120])
ylim([0 350])
xlabel('体調 [cm]')
ylabel('走る速さ [cm/s]')
legend('データ', '線形回帰', 'Box', 'off')
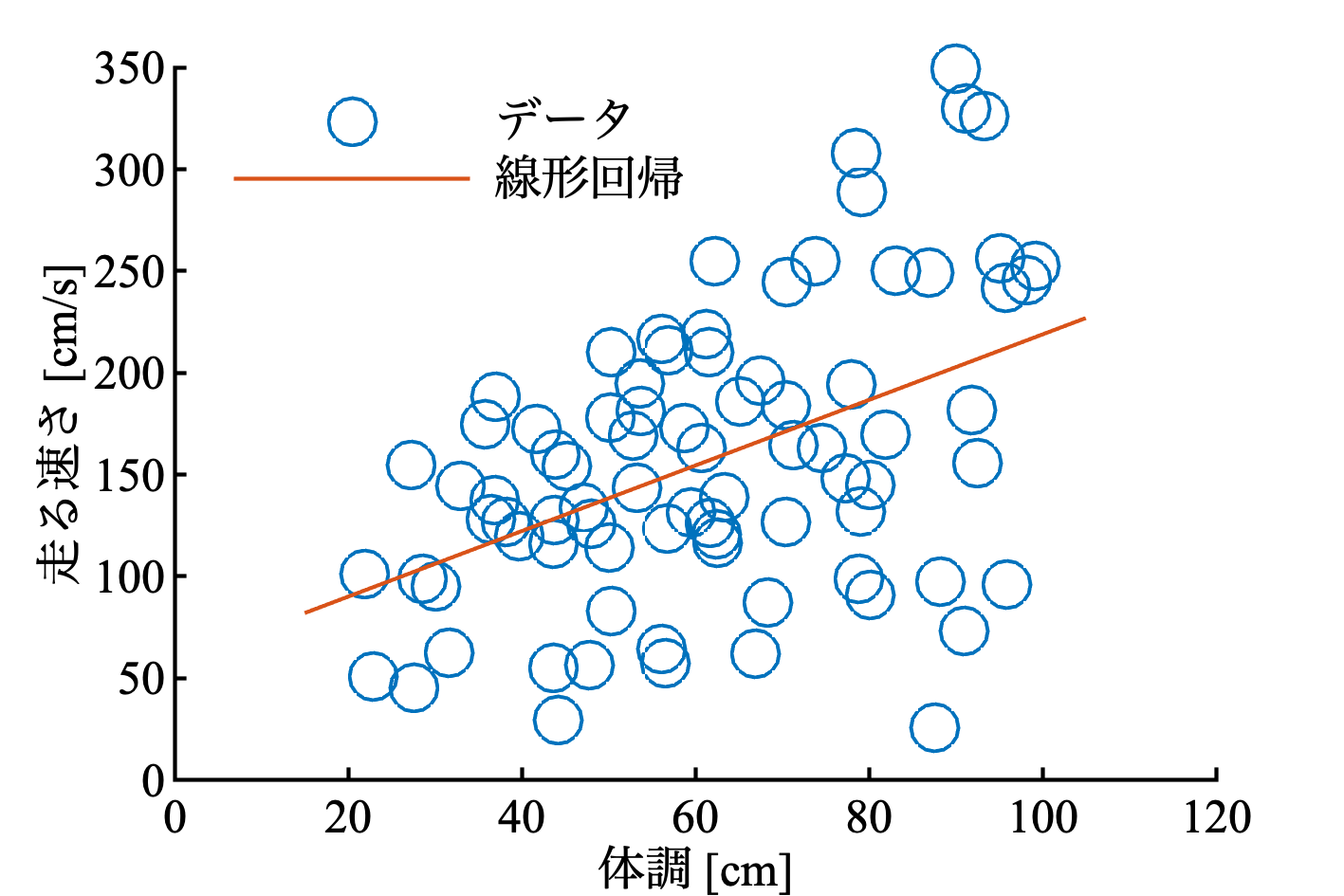
result

どうだろう？ 残差は正規分布にしたがっているだろうか？ 残差を計算してみる.

MATLAB 
res = y - (b(1) + b(2)*x); % 残差
stem(x, res, 'MarkerSize', 3)
xlim([0 120])
ylim([-150 150])
xlabel('体調 [cm]')
ylabel('残差')
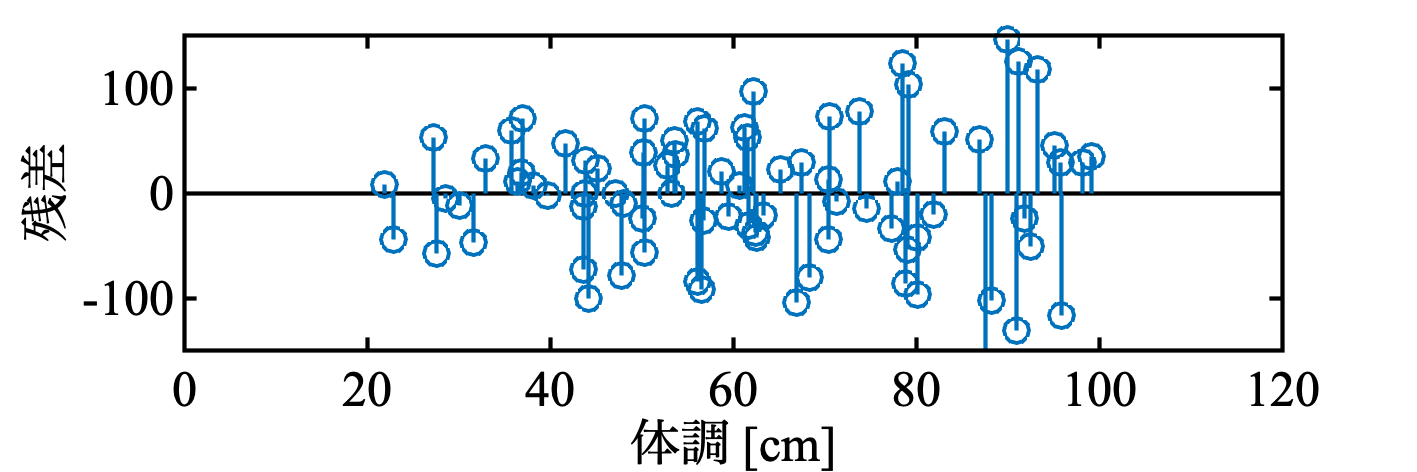
result

明らかに, 分散が一定ではない.

学習済みのモデルからデータを生成してみる

今, 我々のもモデルは以下の形をしている.

\begin{align}\large{ y = b(1) + b(2)x + \varepsilon, \quad \varepsilon \sim \mathcal{N}(0, \sigma^2). \notag }\end{align}
この式に, 推定したパラメータ ( $\sigma$ はstd(res) で計算 ) を代入すると,
\begin{align}\large{ y = 57.84 + 1.61x + \varepsilon, \quad \varepsilon \sim \mathcal{N}(0, 63.78^2). \notag }\end{align}
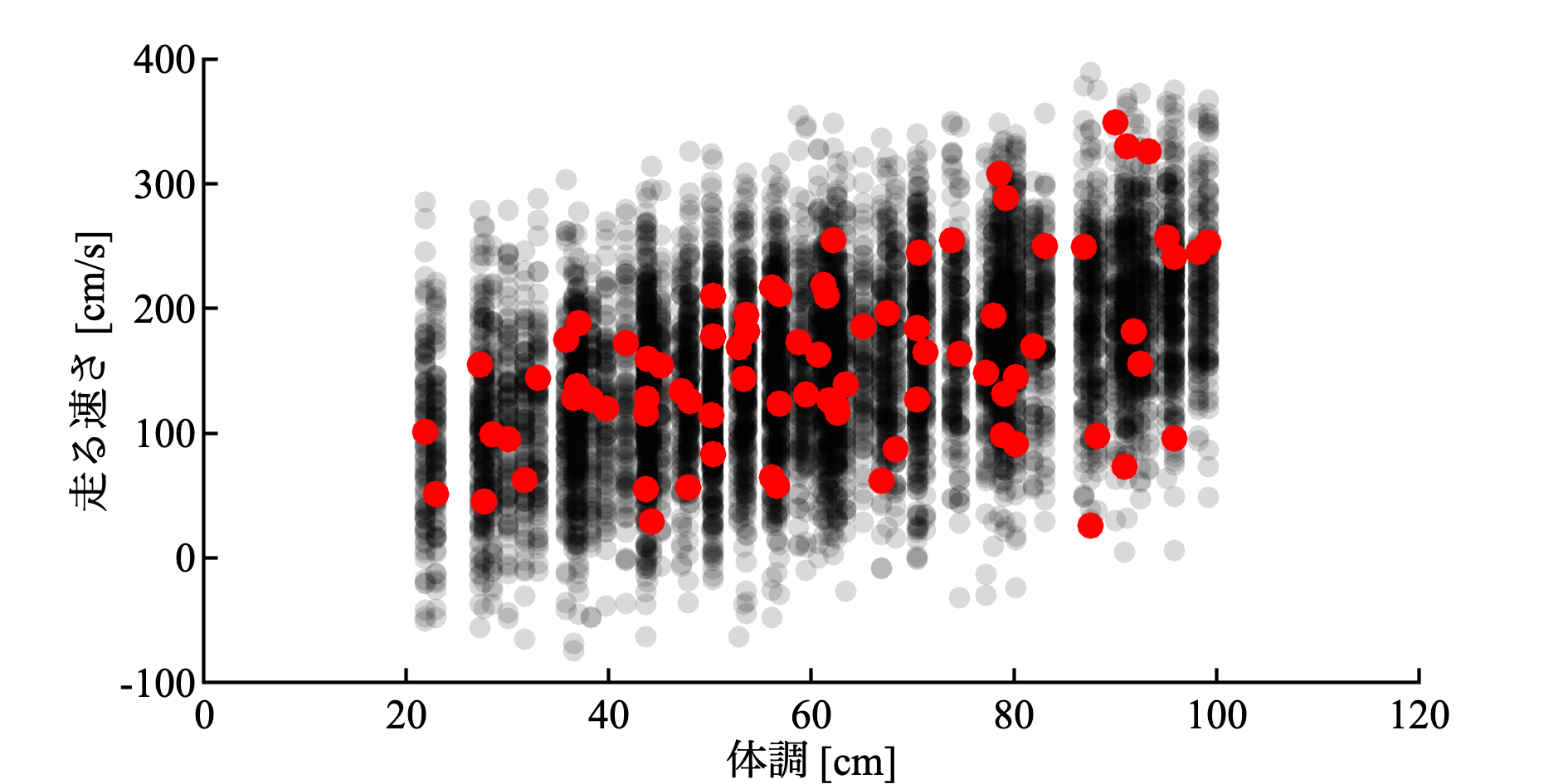
となる. このモデルからたくさんサンプルを作ってみる. モデルがデータと合っていたら, データの分布 ( ちらばり具合 ) が原データと同じ感じになるはずである. 100回原データの体長に対する実現値を発生させ, 透過 ( 'MarkerFaceAlpha' ) させて重ねた. 原データは赤丸で示している.

MATLAB 
for I = 1:100
    rng('shuffle')
    y_est = b(1) + b(2)*x;
    y_est = y_est + randn(L, 1) * std(res);
    scatter(x, y_est, 10, 'k', 'filled', 'MarkerFaceAlpha', 0.15); hold on
end
scatter(x, y, 15, 'r', 'filled'); hold off
xlim([0 120])
ylim([-100 400])
xlabel('体調 [cm]')
ylabel('走る速さ [cm/s]')

どうだろうか？ 原データは, 生成されたデータのばらつきの範囲に入っていて, とんでもなく悪いモデルでは無いと思うが, 以下のような不一致もある.

  • ｘ ( 体長 ) が小さいあたりでは, モデルに対してデータの分散が小さい.
  • ｘ ( 体長 ) が大きいあたりでは, モデルに対してデータの分散が大きい.
  • ｙ ( 走る速さ ) が負の値になっている実現値がある.

実際, このデータは, ｘの増加とともに誤差分散が大きくなるように作っている. できたら, モデルを改良したい. より, 複雑なモデルについては, 今後扱うかもしれない. 今回は, このように乱数をうまく使って, 作ったモデルからデータを擬似的に生成 ( シミュレーション ) できるということを覚えておいてほしい.

result

データ

セミナーで使ったデータはここをクリック.

また, 以下のコードでこのデータを生成することもできる ( 以下のコードから, データの分散が定数ではないことに気づいてほしい ) .

MATLAB 
rng(1234)
N = 100;
scale = 100;
f = @(x) 2*x + 30;
x = rand([N 1])*100;
x = x(x>20);
L = length(x);
y = f(x) + randn(L, 1) .* x;

この記事のTOP    BACK    TOP