『ゼロからできるMCMC』 Chapter7 巡回セールスマン問題をJuliaで

最終更新：2021/08/19

『ゼロからできるMCMC』 Chapter7 巡回セールスマン問題 ( traveling salesman problem、TSP ) のコードを, 練習を兼ねてJuliaで書いてみました. 素朴なアルゴリズム, 焼きなまし法, レプリカ交換法を使います. また, 詳細なことを書くと著作権的にだめな気もするので, 解説などはありません.

注：僕の不注意で, 全て巡回しないセールスマンになってしまっています！「最短距離で全ての街を回ってもとの街に戻る」ではなく，「最短距離で全ての街を回る」が問題設定となっていますが，本質的にはそんなに変わらないと信じています.

Julia Version 1.6.2

この記事で用いたライブラリ.

Julia

using Plots
using Distributions
using Random: seed!
using LinearAlgebra
using StatsBase
using Combinatorics
using BenchmarkTools
using Profile
using ProgressMeter

TSPの問題設定と総当たり法

問題設定

名前から想像がつくように, 巡回セールスマン問題 ( TSP ) はN個の街を効率よく巡回するルートの中で総移動距離が最小となるルートを見つける組み合わせ最適化問題である. 始点をきめていても, 総当りで調べると $(N-1)!/2$ 通りあるので爆発的に組み合わせ数が増えてしまう. まず, この節では $N＝12$ として問題をたててみる. ランダムにX座標とY座標をサンプルして, 以下のような12の都市を作った. 変数citiesの第1列にX座標を, 第2列にY座標を格納している.

Julia

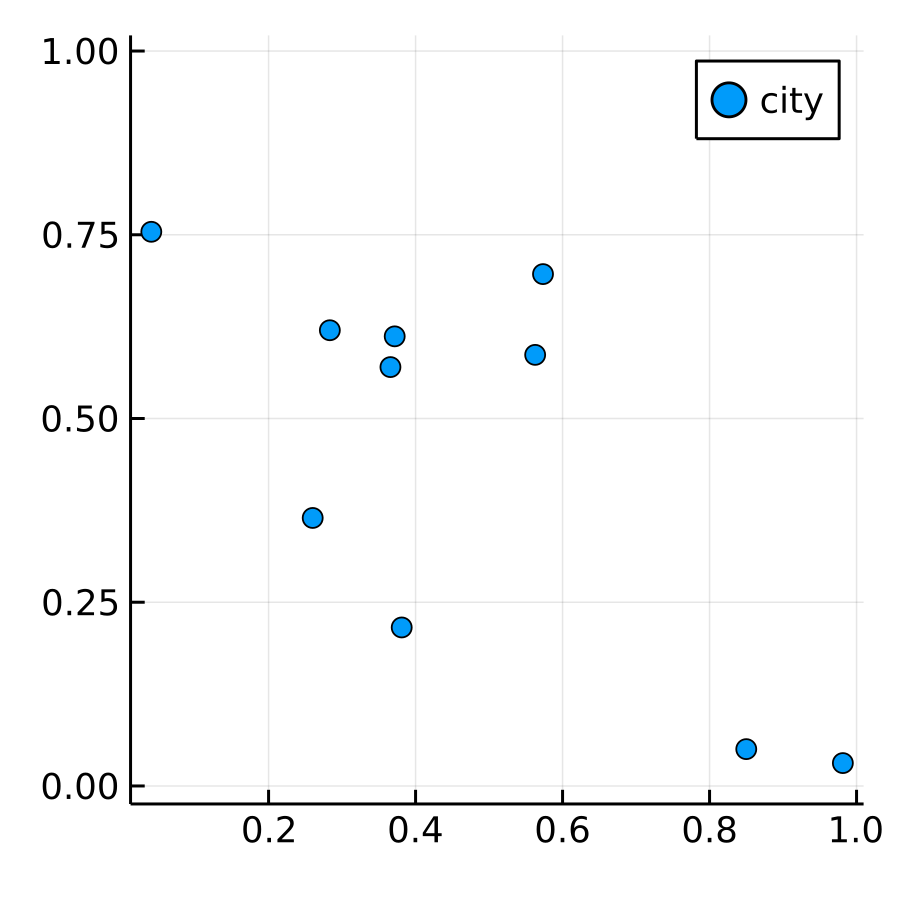
Random.seed!(12345)
N = 12
cities = rand(N, 2)
p = scatter(cities[:, 1], cities[:, 2], label="city", aspect_ratio=:equal, dpi=300, size=(300, 300))

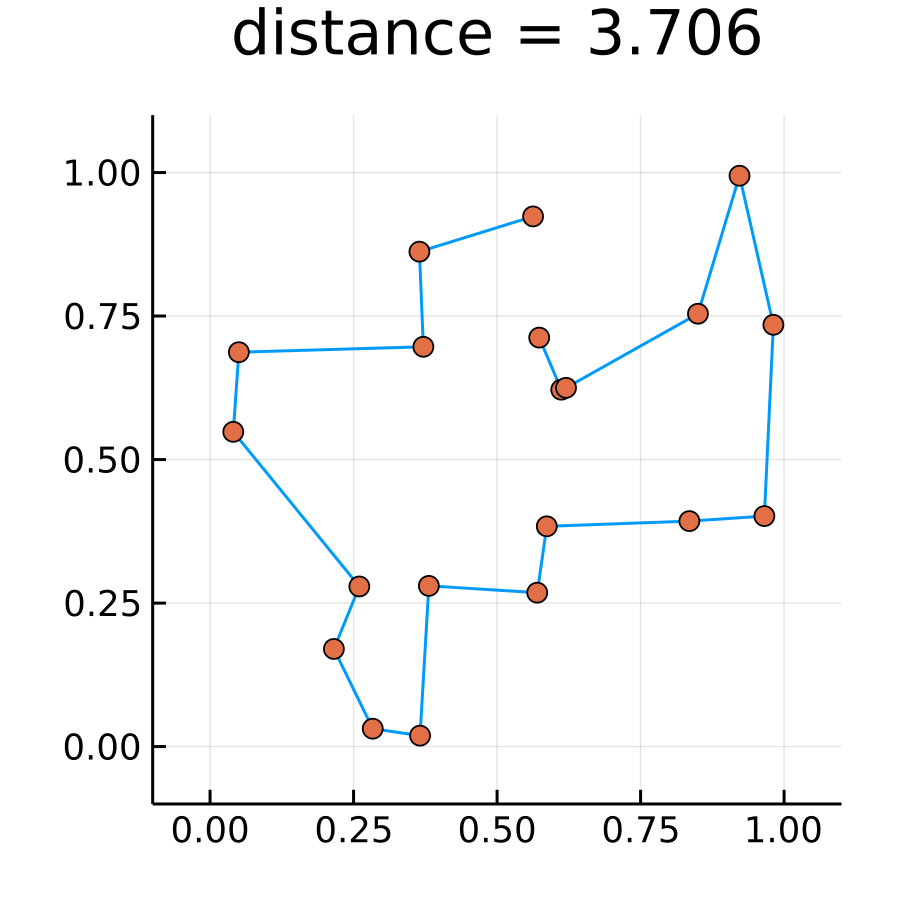
ルートrouteを与えると距離を返す函数calcDistance, とそれをプロットする函数plotRouteを作り, 適当なルートを与えてみる. ここでは, 非復元抽出を行うためにStatsBase.jlのsample函数を使っている. 以下のような巡回ルートでは, 距離が6.045となった.

Julia

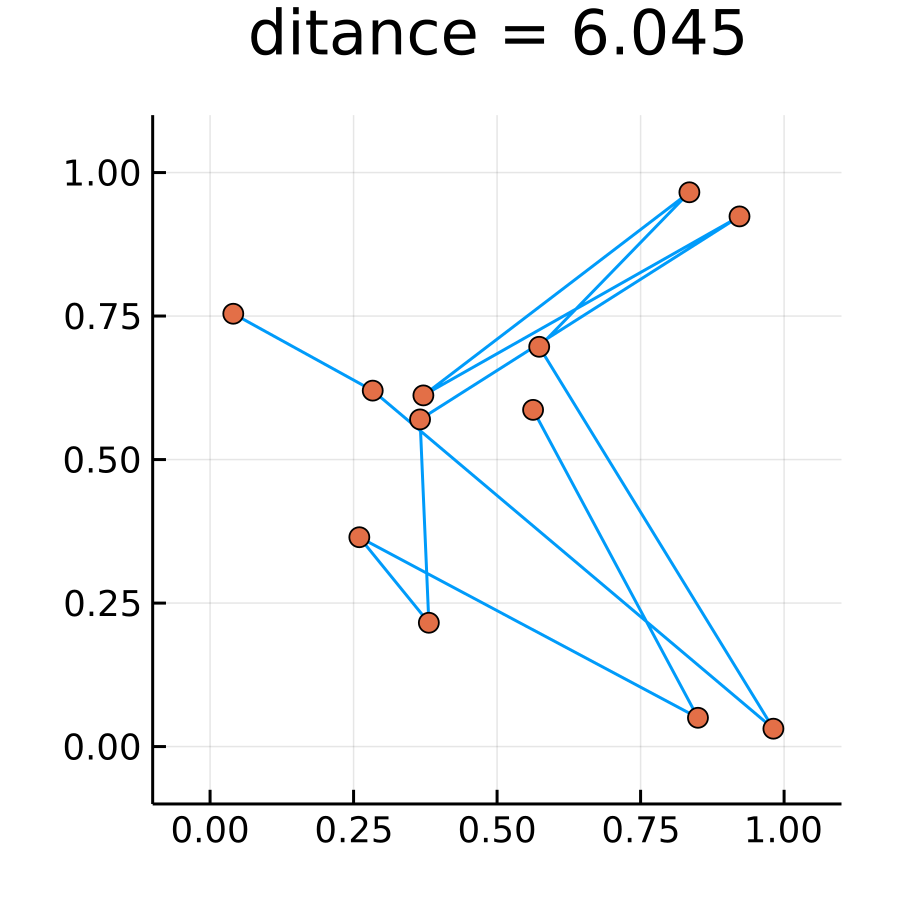
route = sample(2:N, N-1, replace=false)
route = [1; route];
plotRoute(cities, route)
julia> route
12-element Vector{Int64}:
  1
  2
  8
  5
  6
  9
  3
  7
 11
 12
  4
 10

# ルートrouteを与えると距離を返す函数
function plotRoute(cities, route)
    L = length(route)
    X = [cities[I, 1] for I in route]
    Y = [cities[I, 2] for I in route]
    plot(X, Y, aspect_ratio=:equal, label="route", leg=:none, dpi=300, size=(300, 300))
    scatter!(cities[:, 1], cities[:, 2], label="city")
    xlims!(-0.1, 1.1)
    ylims!(-0.1, 1.1)
    d = calcDistance(cities, route, L)
    title!("ditance = $(round(d, digits=3))")
end

# ルートをプロットする函数
calcDistance(cities, route, L) = sum([norm([cities[route[I+1], 1]-cities[route[I], 1], cities[route[I+1], 2]-cities[route[I], 2]]) for I = 1:L-1])

総当りで厳密解を求める

以下のような, 総当りで厳密な最短ルートを求める函数を作った.

Julia

function exactMinRoute(cities)
    N = size(cities, 1)
    perm = permutations(2:N)
    minDist = 100.0
    minRoute =  Vector(1:N)
    route =  Vector(1:N)
    for p in perm
        route[2:N] = p
        d = calcDistance(cities, route, N)
        if minDist > d
            minRoute .= route
            minDist  = d
        end
    end
    @show minDist
    return minRoute, minDist
end

厳密な最短ルートは以下となった. ここで, 全てのルートを虱潰しに調べるためにCombinatorics.jlのpermutation函数を用いていいる.

Julia

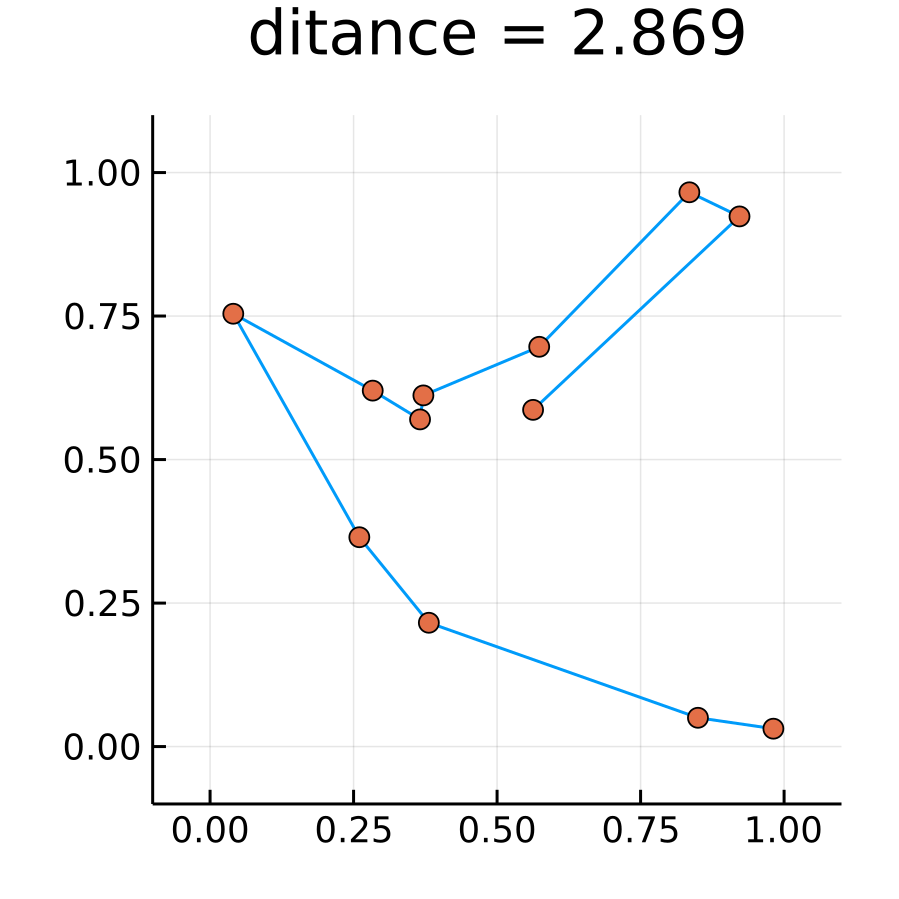
@time minRoute, d = exactMinRoute(cities) # 26 seconds with N = 12
>>  26.914316 seconds (598.77 M allocations: 60.077 GiB, 18.33% gc time)
plotRoute(cities, minRoute)

N=10程度なら一瞬だったが, 12では26秒, 15にすると15分まっても終わらなかった.

素朴なアルゴリズム

アルゴリズムとコード

教科書p.175の素朴なアルゴリズムを使ってみる. これは, 初期ルートを適当に与えて, 適当に2つの都市を交換し, 距離が短くなればそのルートを採用, 短くならなければ元のルートにもどる, という操作を繰り返す手法である. もちろん, 局所解に陥るおそれがある.

Julia

function naiveTSP(cities, iter)
    N = size(cities, 1)
    init = sample(2:N, N-1, replace=false);
    route = [1; init]
    distances = zeros(iter)
    distances[1] = calcDistance(cities, route, N)
        
    for I = 2:iter
        
        oldroute = copy(route)
        swapCoords = sample(2:N, 2, replace=false)
        route[swapCoords[1]], route[swapCoords[2]] = route[swapCoords[2]], route[swapCoords[1]]
        newDist = calcDistance(cities, route, N)
        if newDist < distances[I-1]
            distances[I]  = newDist
        else
            distances[I] = distances[I-1]
            route = copy(oldroute)
        end
    end
    # display(minimum(distances))
    return route, distances
end

一回の計算

繰り返し回数を10^5回にして計算してみた. 以下のような結果となった. 厳密解にはいきつかなかった.

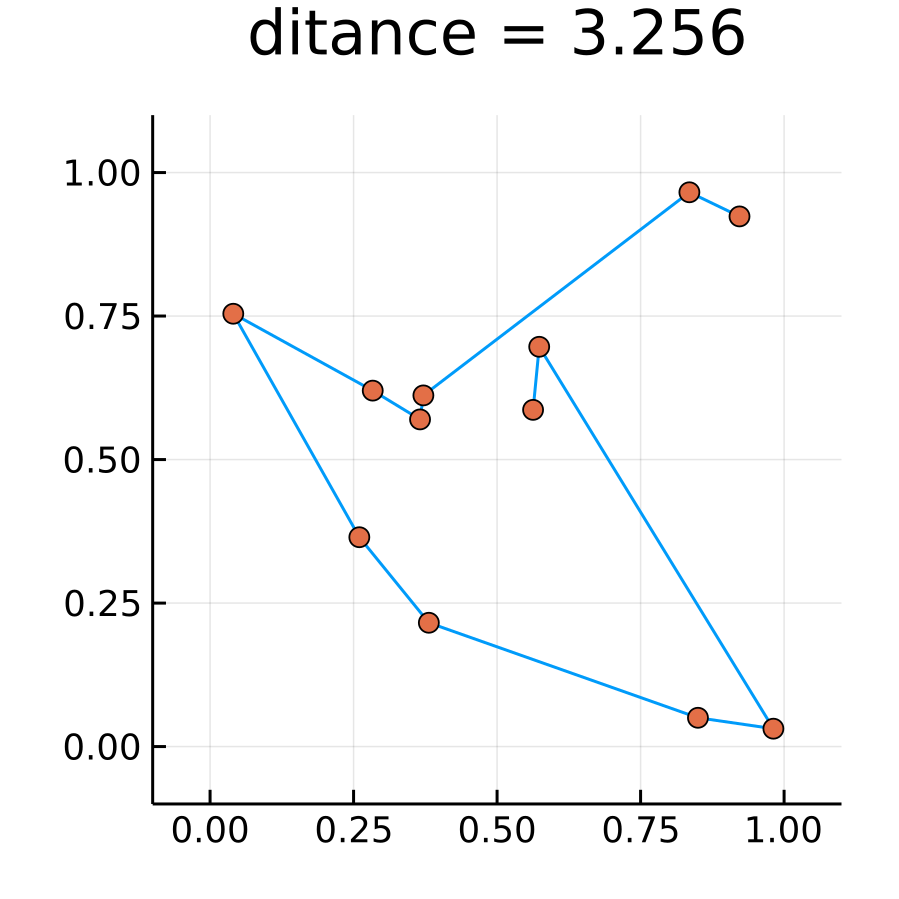
10^5回のイテレーションの中で最小距離がどのように遷移したのかを確認してみる. するとなんと最初の250回くらいですでに局所解に捕まっていたことがわかった.

Julia

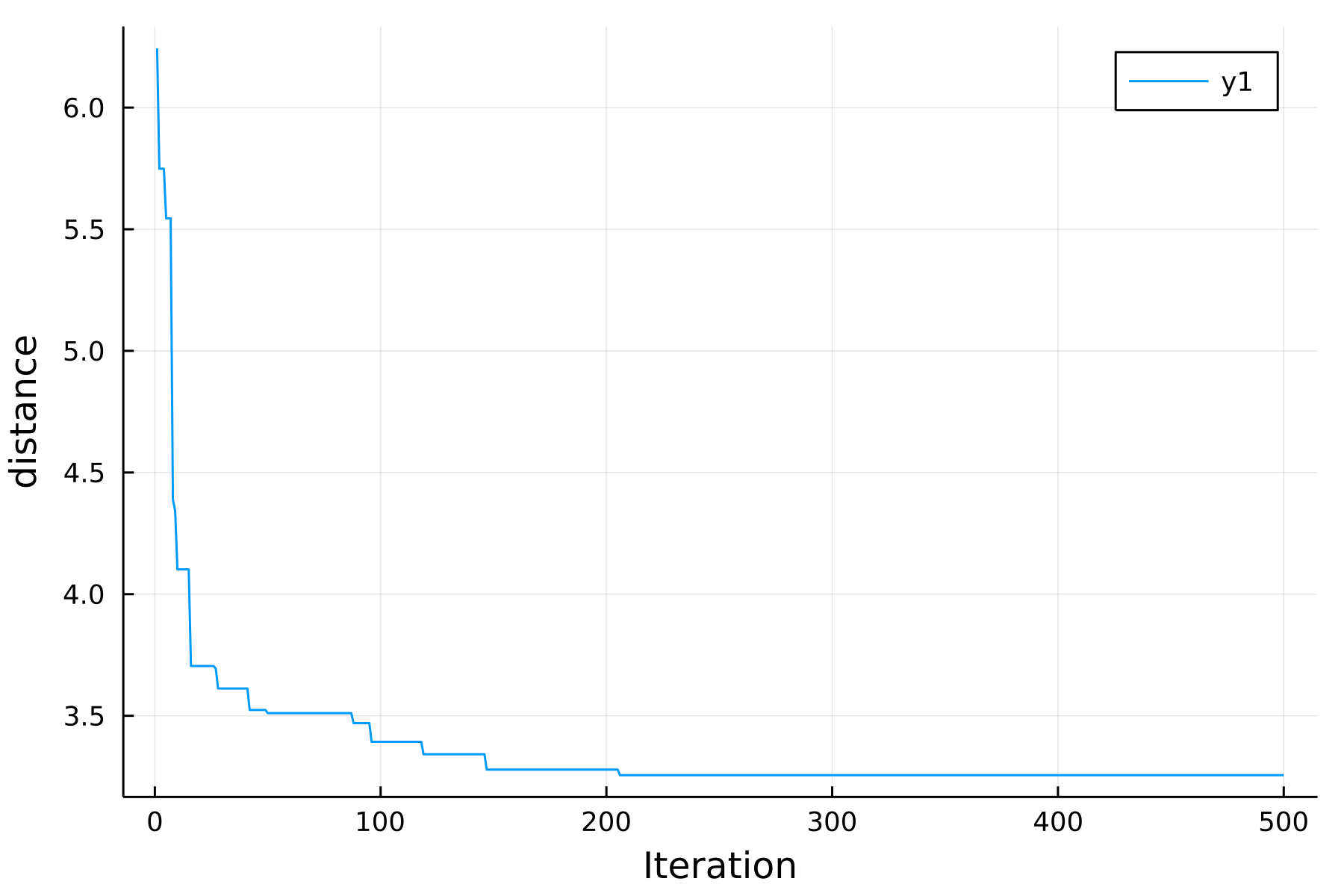
iter = 10^5
@time route, d = naiveTSP(cities, iter);
plotRoute(cities, route)
plot(d[1:500], xlabel="Iteration", ylabel="distance", dpi=300, legend=:none)

初期値を変えての計算

ならば, 大きな回数回すのではなく, 小さな回数で初期値を変えて何度も回すのがいいのではないか. 試してみた.

一回のイテレーション回数を1000回にして100回まわしてみた. 100回それぞれの最小値を取得し, 小さい順にソートした結果が以下である. 数回は無事最小値 ( 2.869 ) に辿り着いている. 計算時間も 0.06秒程度で, 27秒と比べると大幅に下げることができた. もちろん局所解に全て捕われる可能性もあるが, 実用的な手法だと感じた.

Julia

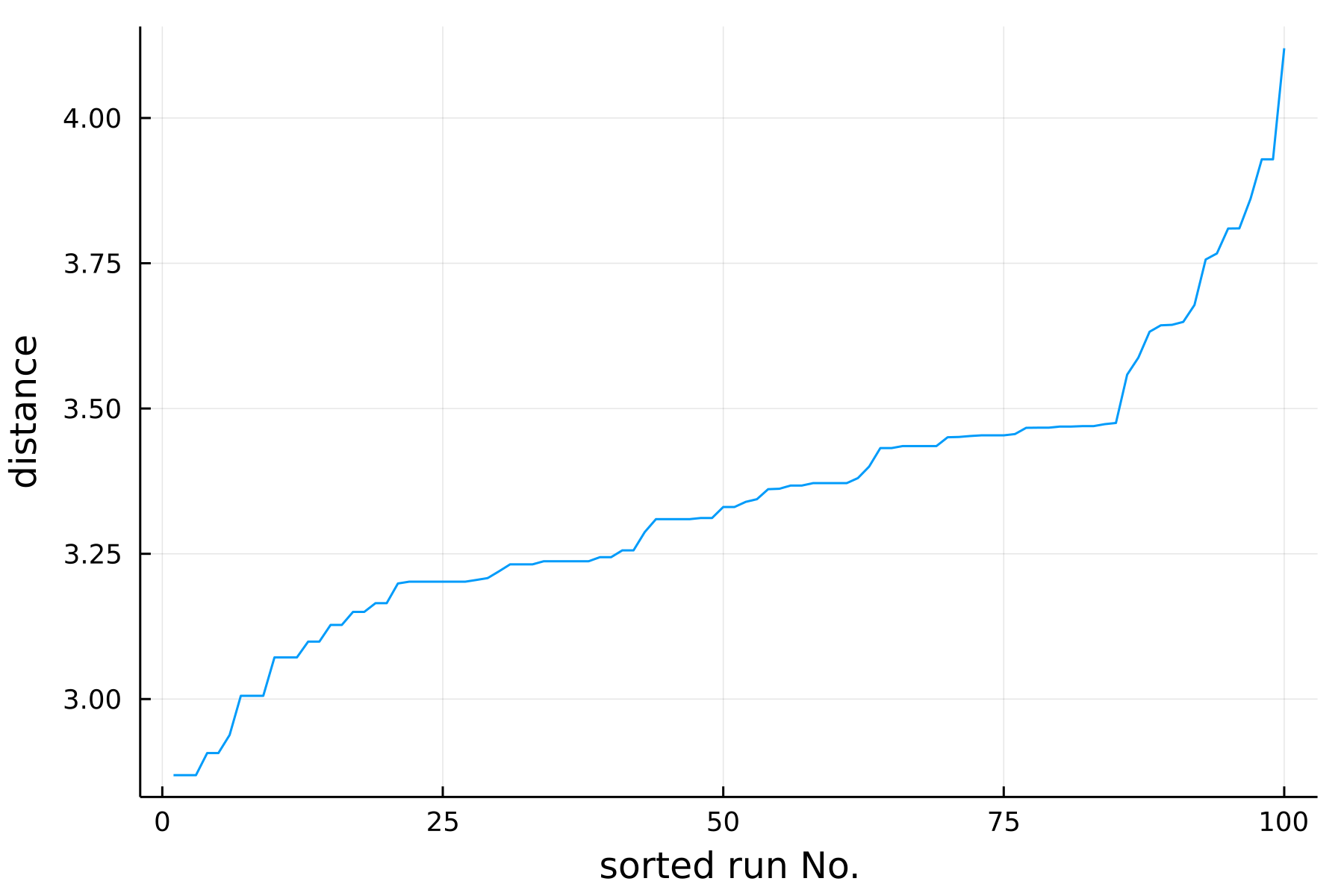
temp = zeros(100)
iter = 10^3
@time for I = 1:100
    route, d = naiveTSP(cities, iter);
    temp[I] = d[end]
end
>> 0.066487 seconds (1.50 M allocations: 160.790 MiB, 15.38% gc time)
plot(sort(temp), xlabel="sorted run No.", ylabel="distance", dpi=300, legend=:none)

20都市にチャレンジ

この方法を使えば, 総当りでは到底計算できなさそうだったN=20でもそれらしい結果がえられた.

Julia

Random.seed!(12345)
N = 20
cities = rand(N, 2)
temp = zeros(100)
iter = 10^4
minRoute20 = collect(1:20);
minD = 100.0
@time for I = 1:100
    route, distances = naiveTSP(cities, iter)
    d = distances[end];
    if d < minD
        minD = d
        minRoute20 .= route
        temp[I] = d[end]
    end
end
plot(sort(temp), xlabel="sorted run No.", ylabel="distance", dpi=300, legend=:none)
plotRoute(cities, minRoute20)

焼きなまし法

コード

焼きなまし法 ( Simulated Annealing ) に関してはレプリカ交換法の前置きとして書かれており, 特に例もなかったのでサラッとすます. 特に, 温度の最大値や下げ方についてはわからなかったので ( 調べたらいいだけだけど ) 適当に試行錯誤で行った. アルゴリズム自体は驚くほど簡単で, コードもシンプル. ただ, このコードは遅い.

Julia

function yakinamashi(cities, iter, Tlist)
    N = size(cities, 1)
    # ルートの初期値をランダムにきめる
    init = sample(2:N, N-1, replace=false)
    route = [1; init]
    oldRoute = copy(route) 
    # 採択率を計算するための採択カウンタ
    naccept = 0
    
    for T in Tlist # 温度を帰る
        for I = 1:iter # それぞれの温度でiter回サンプリング
            oldRoute .= route
            actionInit = calcDistance(cities, route, N)/T　# 作用がこのように定義される, 普通のメトロポリス法
            
            # ルートを更新
            swapCoords = sample(2:N, 2, replace=false)
            route[swapCoords[1]], route[swapCoords[2]] = route[swapCoords[2]], route[swapCoords[1]]
            action = calcDistance(cities, route, N)/T
            
            # Metropolis tests
            exp(actionInit - action) > rand() ? naccept += 1 : route .= oldRoute 
        end
    end
    
    display("accepted rate is $(100*naccept/(length(Tlist)*iter)) %")
    
    return route
end

12都市

上と同じ12都市でやってみた. 色々条件を変えてこれくらいなら十分かな, という値でのシミュレーションを以下に示す.

Julia

Tlist = collect(5:-0.01:0)
iter = 10000

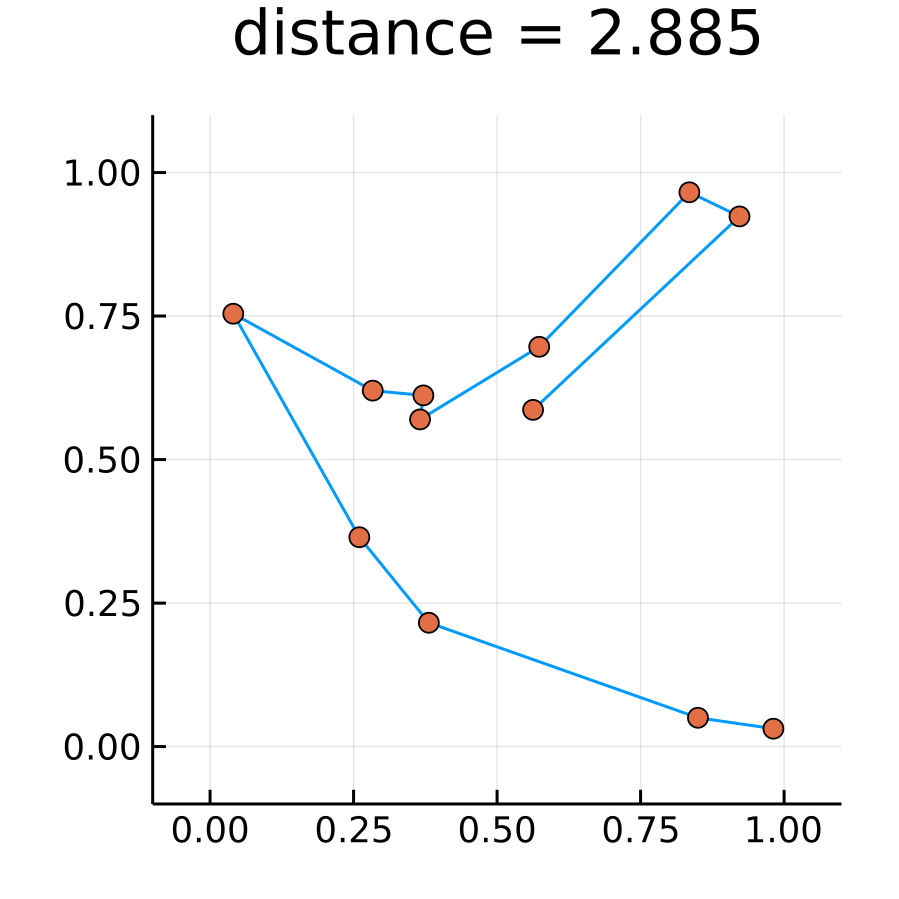
つまり温度を5から0.01刻みで0まで下げて, それぞれの温度で10000回のサンプリング ( Metropolis法 ) を行う. 次のように, Random.seed!(12345)の場合は厳密解に近い値に辿り着いた. もちろん, 乱数の種を変えるとコロコロと結果は変わるが, あまりひどいものにはならなかった.

Julia

Random.seed!(12345)
@time sampledRoutes = yakinamashi(cities, iter, Tlist) 
>> "accepted rate is 83.16135728542915 %"
>> 6.922386 seconds (125.25 M allocations: 11.945 GiB, 24.48% gc time)
plotRoute(cities, sampledRoutes)

思い切って100都市

10分くらいかかったし, 交点があり確実に大域的局所解ではないが, 十分いい感じだと思う. ぜひ, コードを高速化したい.

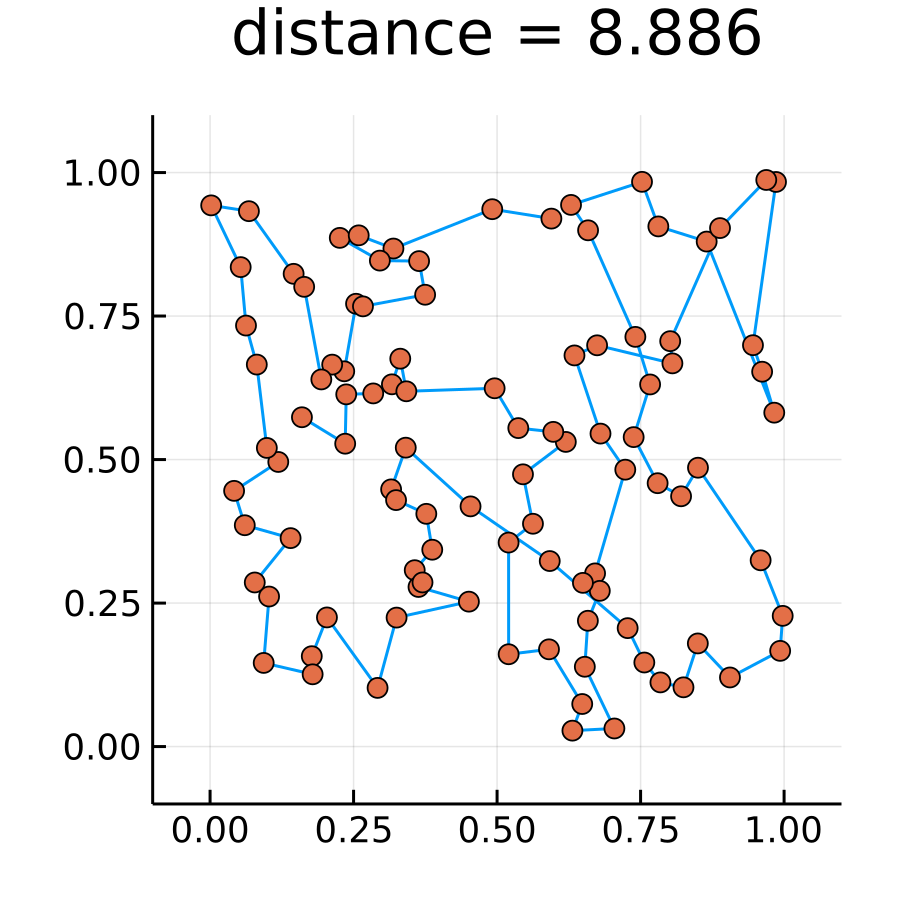
レプリカ交換法

コード

焼きなまし法で作った温度が可変なメトロポリス法のコードがそのまま使える. 違うのは, レプリカを交換するところだけ. それより, 難しかったのは @code_warntypeで赤文字をださないようにすることなど, Juliaプログラミングの過程. 下のコードも相当汚いと思う. なんとか早く計算できるようにしたいが, とりあえずはこれでちゃんとした結果がでたので公開する.

ここで, βに逆温度をベクトルとして渡す. そして, そのベクトルの要素の数がレプリカの数となる. それぞれのレプリカについてMetropolis法をiter回行う. そして, 毎Metropolis法ごとに, レプリカ交換の条件をみたす組の中からランダムに一つ選び, レプリカを交換する. 同時に, 最も逆温度が大きいレプリカについてその時点までで距離が最小となったルートをminRouteに保存する. perOutput回に一度, 最大逆温度のレプリカのルートと距離を保存する.

Julia

function replicaExchangeTsp(cities, iter, β, perOutput=1000)
    
    # 定数
    Δβ = diff(β)            # 温度の差分, レプリカ交換の際に使う
    N  = size(cities, 1)    # 都市の数
    M  = length(collect(β)) # レプリカの数
    
    # 初期値 全てのレプリカで1,2,...という順路
    routes =  collect(1:N) .* ones(Int, 1, M) 
    
    # preallocation
    oldRoute        = routes[:, 1]                      # 各iterでのルートのバックアップを格納するため
    routeOut        = Matrix{Int64}(undef, N, 1);       # perOutput毎に最大逆温度を持つレプリカのルートを格納するため
    routeOut[:, 1] .= oldRoute  
    distOut         = Vector{Float64}(undef, 1)         # perOutput毎に最大逆温度をもつレプリカのルートの距離を格納
    distOut         = calcDistance(cities, oldRoute, N) 
    rs              = fill(distOut, M)                  # 各レプリカの距離, レプリカ交換の際に使う
    exchange        = 1:M-1                             # 交換するレプリカの候補
    minRoute        = routes[:, 1]                      # 最大逆温度をもつレプリカの距離の最小値
    minDist         = calcDistance(cities, oldRoute, N) # 上記のルート
    
    @showprogress for I = 1:iter
        for m = 1:M # 各レプリカでメトロポリス法

            oldRoute .= routes[:, m]
            rPre      = calcDistance(cities, routes[:, m], N) 
            
            # ルートを更新
            c1, c2        = sample(2:N, 2, replace=false)
            routes[:, m] .= swapcol(routes[:, m], c1, c2)
            rPost         = calcDistance(cities, routes[:, m], N)
            
            # Metropolis tests
            exp((rPre - rPost)*β[m]) > rand() ? rs[m] = rPost : routes[:, m] .= oldRoute 
        end
        
        # replica exchange
        bool = exp.(Δβ .* diff(rs)) .> rand(M-1) 
        cand = exchange[bool] # 入れ替えの候補
        m    = cand[rand(1:length(cand))] # 候補から一つ選ぶ 
        swapcol!(routes, m, m+1)
        
        # ここまでの最小値ならルートと距離を保存 ( 最大逆温度をもつレプリカに対して ) 
        if minDist > rs[end]
            minDist   = rs[end]
            minRoute .= routes[:, end]
        end 
        
        # perOutput毎にルートと距離を保存 ( 最大逆温度をもつレプリカに対して ) 
        if mod(I, perOutput) == 0
            routeOut = [routeOut routes[:, end]]
            distOut  = [distOut; rs[end]]
        end
    end
    return Result(routeOut, distOut, minRoute)
end

# ベクトルの要素を交換するようにしている
function swapcol(mat::Vector{Int64}, c1, c2)
    temp    = mat[c1]
    mat[c1] = mat[c2]
    mat[c2] = temp
    return mat
end

# 行列の列を交換する破壊的函数
function swapcol!(mat::Matrix{Int64}, c1, c2)
    temp        = mat[:, c1]
    mat[:, c1] .= mat[:, c2]
    mat[:, c2] .= temp
end

# 結果の構造体
struct Result
    routeOut::Matrix{Int64}
    distOut::Vector{Float64}
    minRoute:: Vector{Int64}
end

12都市

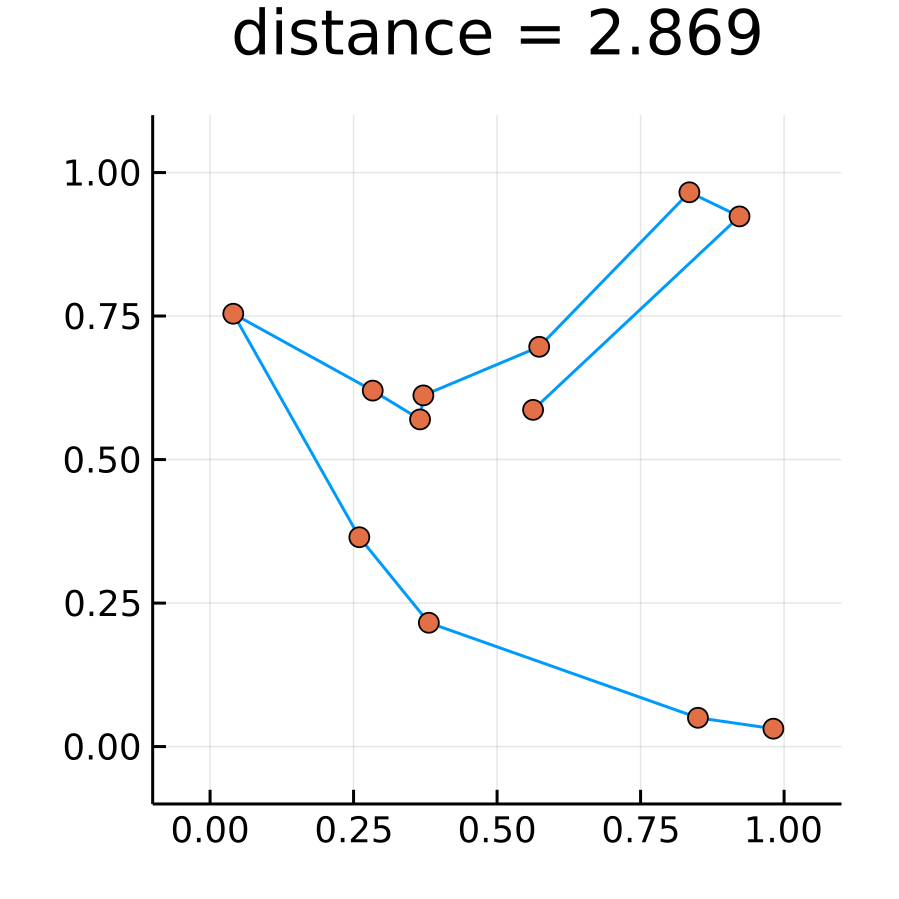
レプリカは教科書とあわせて200に設定. イテレーションは10000回. 厳密解に辿り着いた.

Julia

seed!(12345)
N = 12
cities = rand(N, 2)
iter = 10000
β = 0.5:0.5:100

seed!(12345)
@time res = replicaExchangeTsp(cities, iter, β,  100)
>>   3.102505 seconds (58.08 M allocations: 6.134 GiB, 23.61% gc time)
plotRoute(cities, res.minRoute)

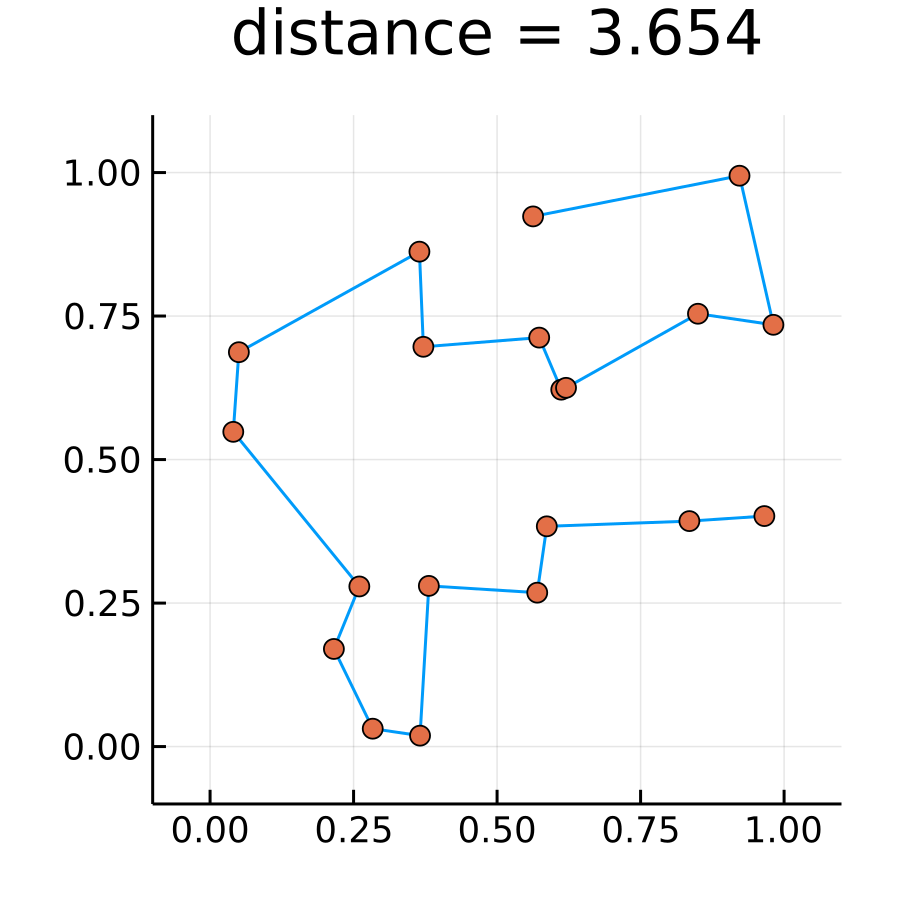
20都市

イテレーションを50000回にして20都市. 厳密解かはわからないが, 素朴なアルゴリズムよりは短い距離となった.

Julia

seed!(12345)
N = 20
cities = rand(N, 2)
iter = 50000
β = 0.5:0.5:100

seed!(12345)
@time res = replicaExchangeTsp(cities, iter, β,  100)
>>   23.725103 seconds (450.37 M allocations: 48.574 GiB, 22.63% gc time)
plotRoute(cities, res.minRoute)

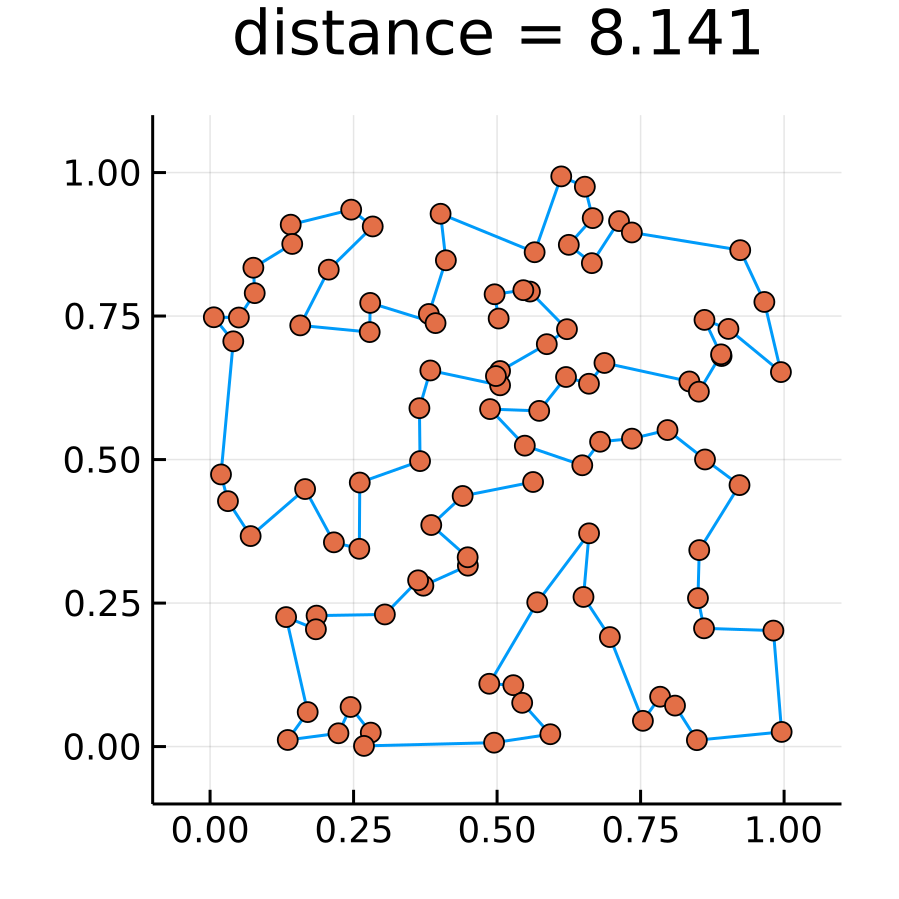
100都市

イテレーションを2,000,000回にして100都市. およそ一時間かかった. 教科書は五千万回回していて, このプログラムを使うと25倍なので25時間くらいかかる. この結果が厳密解かは, . . . わからない. けれども交差もなく, なかなかよいように見える.

Julia

seed!(12345)
N = 100
cities = rand(N, 2)
iter = 2000000
β = 0.5:0.5:100

seed!(12345)
@time res = replicaExchangeTsp(cities, iter, β,  100)
>> 4047.016518 seconds (82.02 G allocations: 9.066 TiB, 21.51% gc time)
plotRoute(cities, res.minRoute)
plot(res.distOut)

最大逆温度のレプリカの距離の遷移はこんなかんじ．

Julia

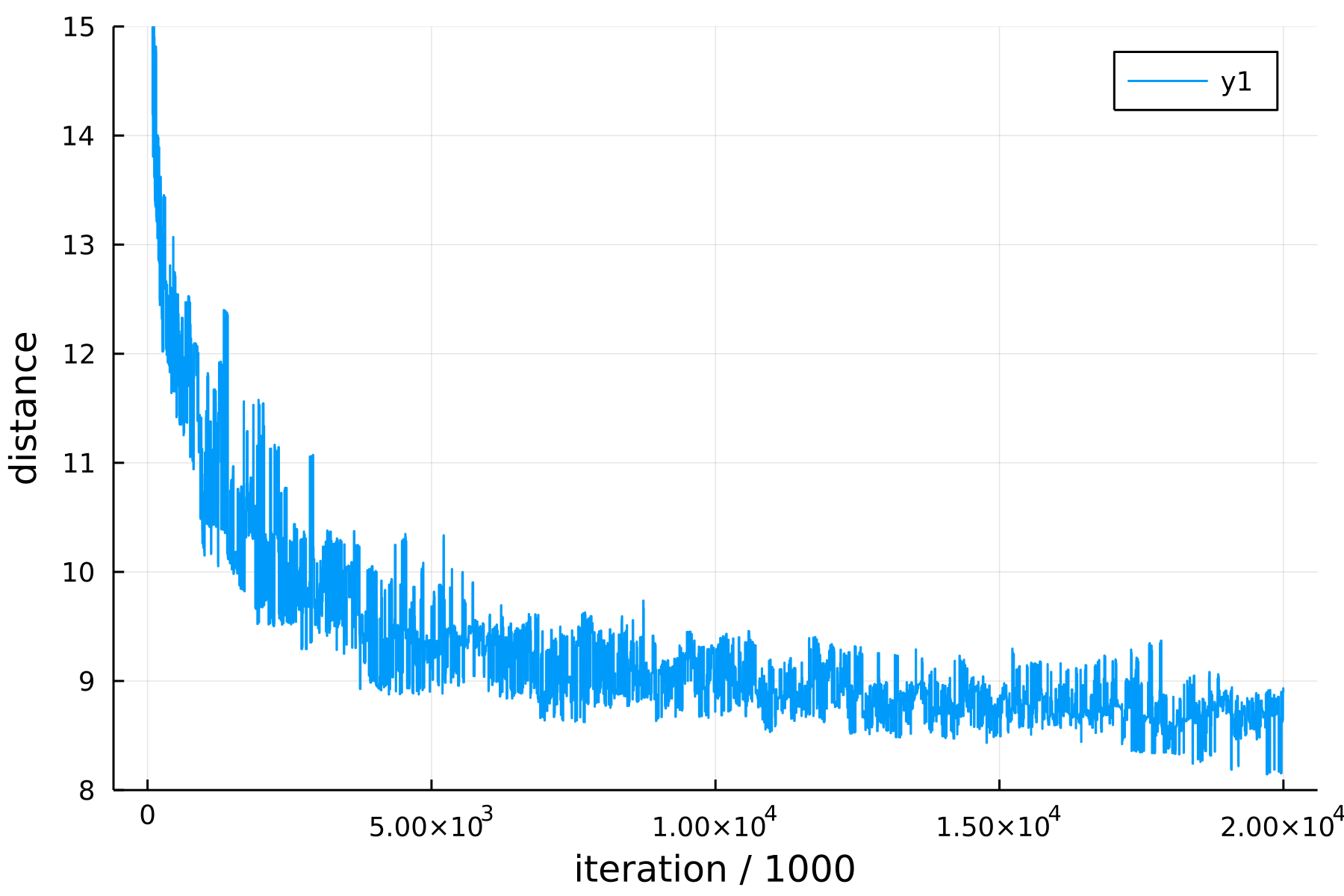
plot(res.distOut, ylims=(8.0, 15.0), xlabel="iteration / 1000", ylabel="distance", dpi=300)

いつか：高速化・並列化したい

この記事のTOP BACK TOP