『ゼロからできるMCMC』 Chapter6 Gibbs SamplingをJuliaで
最終更新:2020/11/24
『ゼロからできるMCMC』 Chapter6 Gibbs Samplingのコードを, 練習を兼ねてJuliaで書いてみました. 詳細なことを書くと著作権的にだめな気もするので, 解説などはありません.
Julia Version 1.5.0
GSを用いた3次元正規分布からのサンプリング
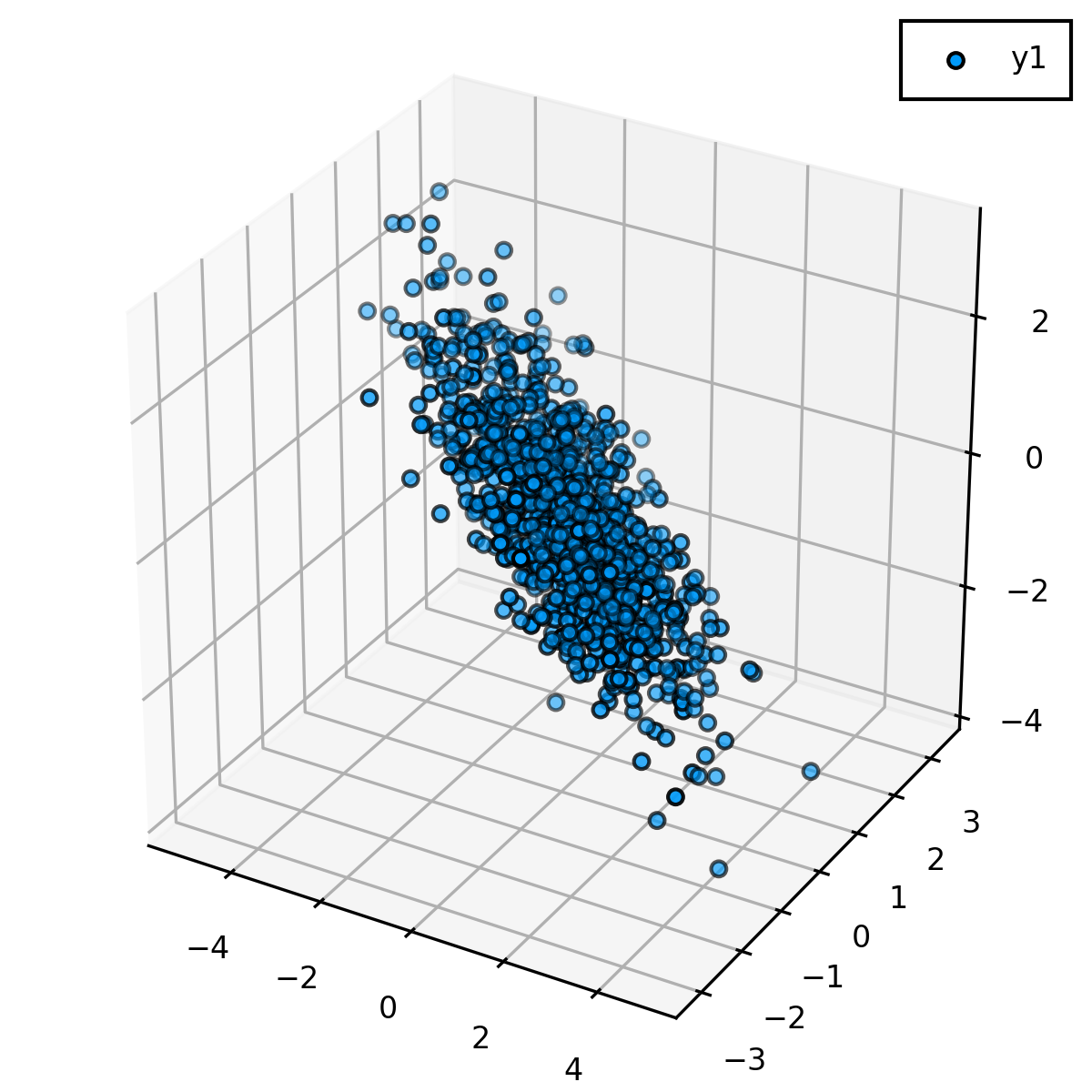
Gibbs Sampling ( GS ) を用いて, 3次元正規分布からサンプルをとります.
Julia
using Plots
using Random:seed!
using Distributions
function gs3dgaussian(;niter=10^3)
# ================= 準備 =================
seed!(12345)
x, y, z = 0.0, 0.0, 0.0 # 初期配位
res = zeros(niter+1, 3) # サンプルを格納する
res[1, :] .= x, y, z
# ========================================
# ================= 更新 =================
σx = 1/sqrt(A[1, 1])
σy = 1/sqrt(A[2, 2])
σz = 1/sqrt(A[3, 3])
μx(y, z) = -y*A[1, 2]/A[1, 1] - z*A[1, 3]/A[1, 1]
μy(x, z) = -x*A[2, 1]/A[2, 2] - z*A[2, 3]/A[2, 2]
μz(x, y) = -x*A[3, 1]/A[3, 3] - y*A[3, 2]/A[3, 3]
for iSample in 1:niter
x = σx*randn() + μx(y, z)
y = σy*randn() + μy(x, z)
z = σz*randn() + μz(x, y)
res[iSample+1, :] .= x, y, z
end
# ========================================
return res
end
# 結果
# 作用にでててくるAᵢⱼを定義
A = [1.0 1.0 1.0;
1.0 2.0 1.0;
1.0 1.0 2.0];
res = gs3dgaussian();
pyplot(fmt=:svg, size=(400, 400))
scatter3d(res[:, 1], res[:, 2], res[:, 3])
PyPlot.savefig("GS_q.png", dpi=300)
多分大丈夫でしょう.