『pythonで学ぶ流体力学の数値計算法』 Chapter 2-7をJuliaで
最終更新:2020/11/28
『pythonで学ぶ流体力学の数値計算法』 Chapter 2-7のコードを, 練習を兼ねてJuliaで書いてみました. 詳細なことを書くと著作権的にだめな気もするので, 詳しい解説などはありません.
Julia Version 1.5.0
Gaussian Hill問題
以下で示される二次元移流方程式を解く.
\begin{align}
\frac{\partial q}{\partial t} +
c\frac{\partial q}{\partial x} +
d\frac{\partial q}{\partial y} = 0
\end{align}
初期状態は, 教科書にならい, ガウシアンにした. Distributions.jlのpdf函数+
多次元正規分布MvNormalを拝借して, 初期状態を作った.
一次元風上差分を使い, 以下のように離散化される.
\begin{align}
q^{n+1}_{j,\,k} = q^{n}_{j,\,k} -
\frac{c \Delta t}{\Delta x} \cdot \left(q^{n}_{j,\,k} - q^{n}_{j-1,\,k}\right)-
\frac{d \Delta t}{\Delta y} \cdot \left(q^{n}_{j,\,k} - q^{n}_{j,\,k-1}\right)
\end{align}
Julia
using Plots
using Distributions
# パラメータ
struct Params
c::Float64
d::Float64
Δt::Float64
Δx::Float64
Δy::Float64
jmax::Int64
kmax::Int64
nmax::Int64
end
# メイン関数
function do_computing(p)
# 初期化
x = collect(range(0.0, p.Δx*(p.jmax-1), length=p.jmax))
y = collect(range(0.0, p.Δy*(p.kmax-1), length=p.kmax))
μ = [maximum(x)/4, maximum(y)/4]
Σ = [maximum(x)/50 0; 0 maximum(y)/50]
f(x, y) = pdf(MvNormal(μ, Σ), [x, y])
q = f.(transpose(x), y)
# 結果を格納する変数
res = zeros(p.nmax, p.jmax, p.kmax)
res[1, :, :] = q
# UPWINDの計算
tmp1 = p.c*p.Δt/p.Δx
tmp2 = p.d*p.Δt/p.Δy
for n = 2:p.nmax
qold = q[:, :]
for k = 2:p.kmax-1
for j = 2:p.jmax-1
q[j, k] = (qold[j, k] - tmp1*(qold[j, k]-qold[j-1, k])
- tmp2*(qold[j, k]-qold[j, k-1]))
end
end
res[n, :, :] .= q
end
return x, y, res
end
実行して, gifにしてみた.
Julia
p = Params(1.0, 1.0, 0.05, 0.1, 0.1, 41, 41, 31)
x, y, res = do_computing(p)
# 図示
anim = Animation()
for n = 1:31
plt = surface(x, y, res[n, :, :], clims=(0.0, 2.0), xlabel="x",ylabel="y")
plt.subplots[1][:zaxis][:lims] = [0, 2]
frame(anim, plt)
end
gif(anim, "test.gif", fps=10)
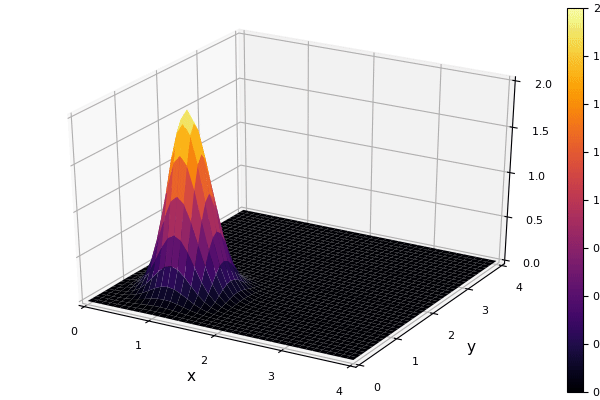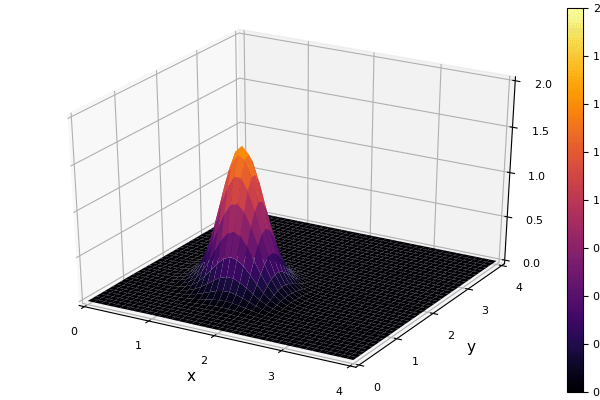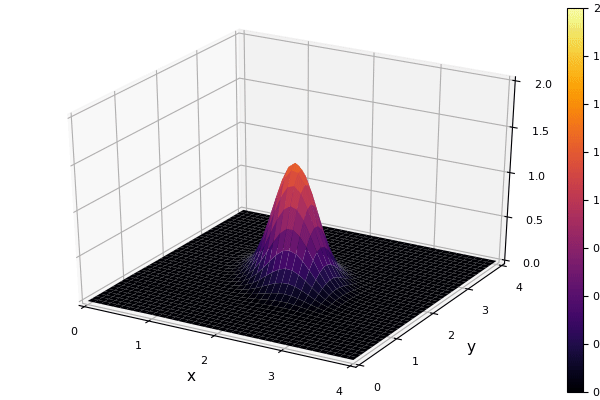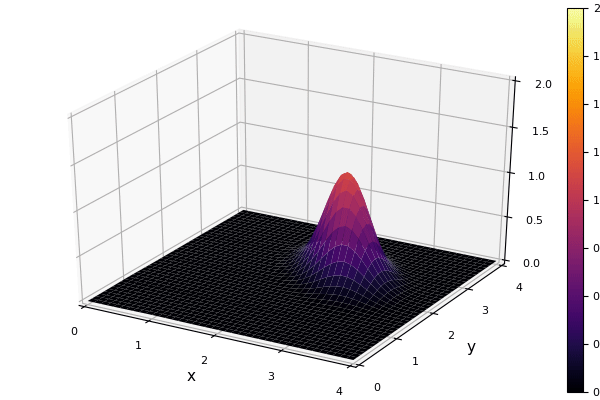
上手く流れてくれた. たしかに, 風上差分による数値粘性のせいで, 減衰している.