『pythonで学ぶ流体力学の数値計算法』 Chapter 2-6をJuliaで

最終更新：2020/11/28

『pythonで学ぶ流体力学の数値計算法』 Chapter 2-6のコードを, 練習を兼ねてJuliaで書いてみました. 詳細なことを書くと著作権的にだめな気もするので, 詳しい解説などはありません.

Julia Version 1.5.0

Murman-Cole法


以下のBurgers方程式を解く.

\begin{align} \frac{\partial q}{\partial t} + q\frac{\partial q}{\partial x} = 0 \end{align}
初期条件(函数init)
\begin{align} \mathrm{I.C.} \:\:q= \begin{cases}q_{1} & x \lt 0\\ q_{2} & x \geq 0\end{cases} \end{align}
保存型で表すと以下になる.
\begin{align} \frac{\partial q}{\partial t} + \frac{\partial}{\partial x} \left( \frac{1}{2}q^2 \right)= 0 \end{align}
Murman-Cole法では, これを以下のように離散化する. (函数do_computing)
\begin{align} q_{j}^{n+1} = q_{j}^{n} - \frac{\Delta t}{\Delta x} (\tilde{f}_{j+1/2}^{\,n} - \tilde{f}_{j-1/2}^{\,n}), \end{align}
ここで, (函数MC)
\begin{align} \tilde{f}_{j+1/2}^{\,n} = \begin{cases} \frac{1}{2}q_{j}^2 & (q_{j}+q_{j+1})/2 \gt 0\\ \frac{1}{2}q_{j+1}^2 & (q_{j}+q_{j+1})/2 \leq 0 \end{cases}. \end{align}

必要な函数群. 関数名を, 教科書と同じにした.

Julia 

# 初期化函数
function init(q1, q2, Δx, jmax)
    xs = -1.0
    x = collect(range(xs, xs+Δx*(jmax-1), length=jmax))
    q = @. q1 * (x<0.0) + q2 * (x>=0.0)
    return x, q
end

# メイン関数
function do_computing(x, q, Δt, Δx, nmax, ff; order=1, interval=2)

    jmax = length(x)
    res  = zeros(jmax, nmax)
    res[:, 1] = q

    for n in 2:nmax
        qold = q[:]
        for j in order+1:nmax-order-1
            ff1 = ff(qold, Δt, Δx, j)
            ff2 = ff(qold, Δt, Δx, j-1)
            q[j] = qold[j] - (ff1-ff2)*Δt/Δx
        end
        res[:, n] = q
    end
    return res
end

# Murman-Cole法の数値流束
function MC(q, Δt, Δx, j)
    ur = q[j+1]
    ul = q[j]
    fr = 0.5*ur^2
    fl = 0.5*ul^2
    c  = 0.5*(ur + ul)
    return 0.5*(fr + fl - sign(c)*(fr-fl))
end

プログラムの実行と結果.

Julia 

# パラメータ
q1   = 1.0;
q2   = 0.0;
Δt   = 0.05;
Δx   = 0.1;
nmax = 21;
jmax = 21;

# 実行
x, q = init(q1, q2, Δx, jmax)
res  = do_computing(x, q, Δt, Δx, nmax, MC)

# 図示
pyplot(fmt=:svg, size=(400, 250))
plot(x, res[:, 1:5:end],
     labels=["t=0" "t=5" "t=10" "t=15" "t=20"],
     color_palette=palette([:red, :blue], 5))
xlabel!("x")
ylabel!("q")
PyPlot.savefig("img/2_6_1.png", dpi=300)
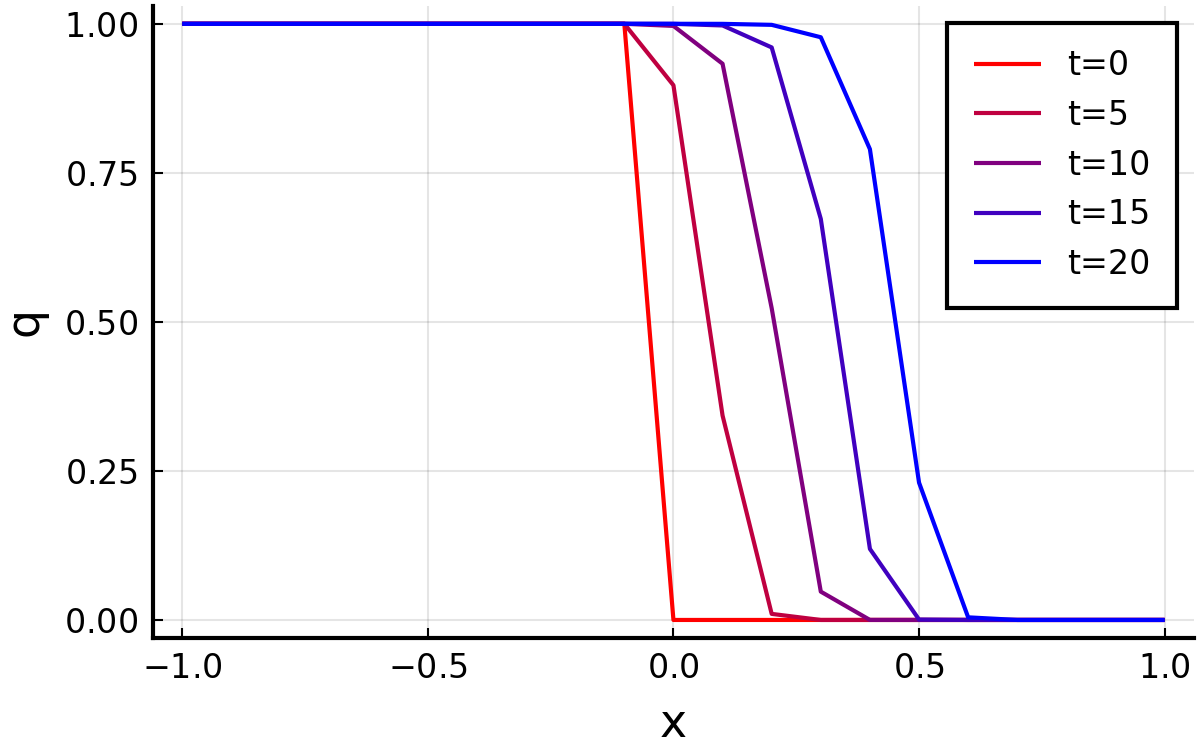
result

教科書と同じ結果担ったように見える.

様々な初期値


p.62 リスト2.13にある初期値を試してみる. 例えば, ケース1なら以下のパラメータを変えるだけ.

Julia 

q1   = 2.0;
q2   = 1.0;

# 実行
x, q = init(q1, q2, Δx, jmax)
res  = do_computing(x, q, Δt, Δx, nmax, MC)

ケース1：\( q_{1}=2.0,\:q_{2}=1.0 \)

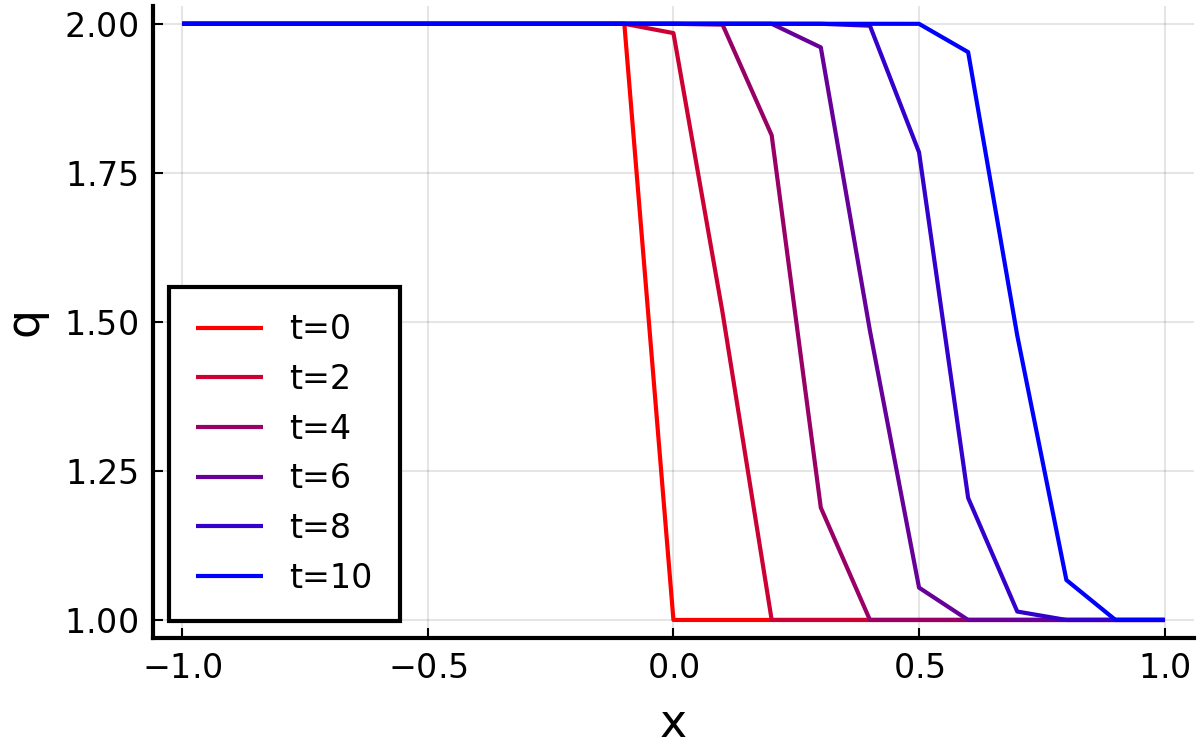
result

ケース2：\( q_{1}=1.0,\:q_{2}=2.0 \)

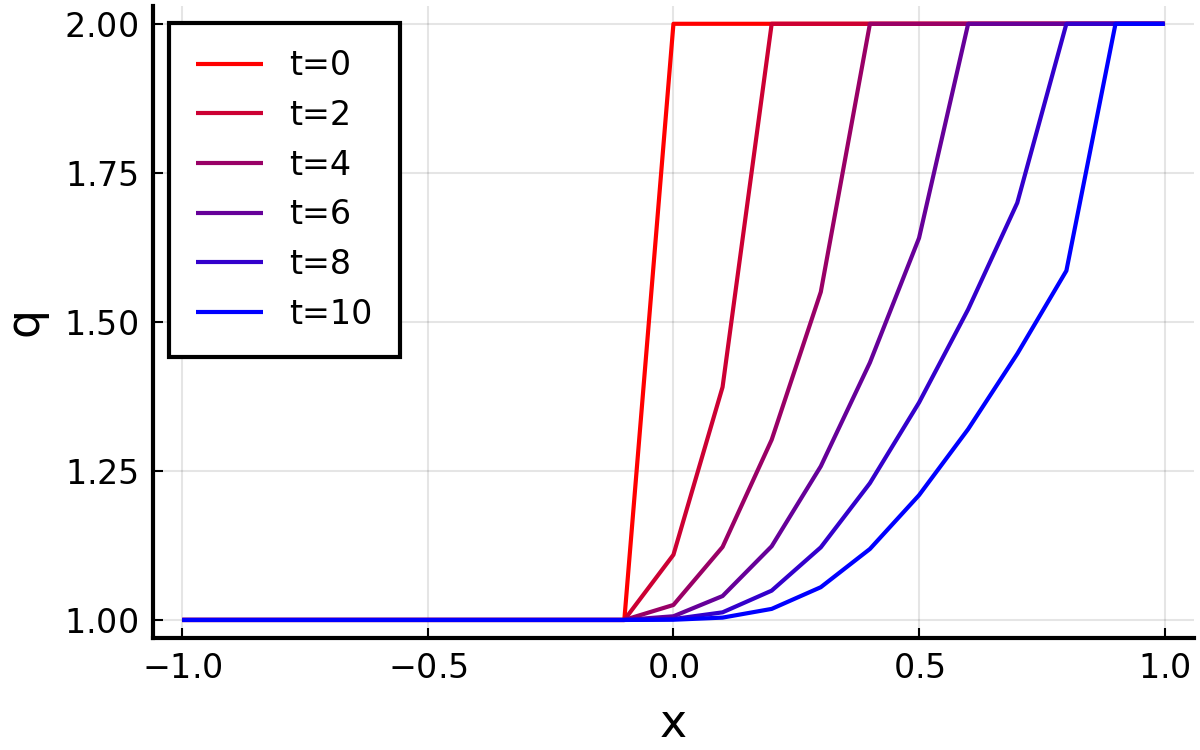
result

ケース3：\( q_{1}=1.0,\:q_{2}=-1.0 \)

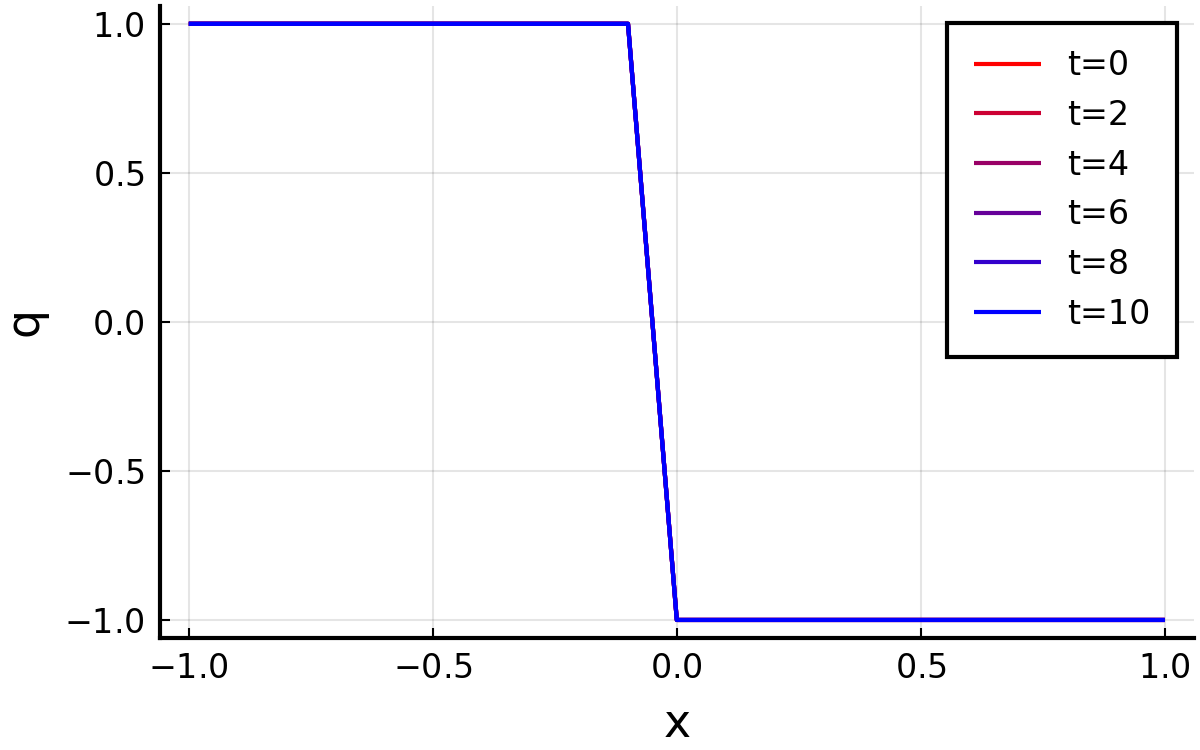
result

ケース4：\( q_{1}=-1.0,\:q_{2}=1.0 \)

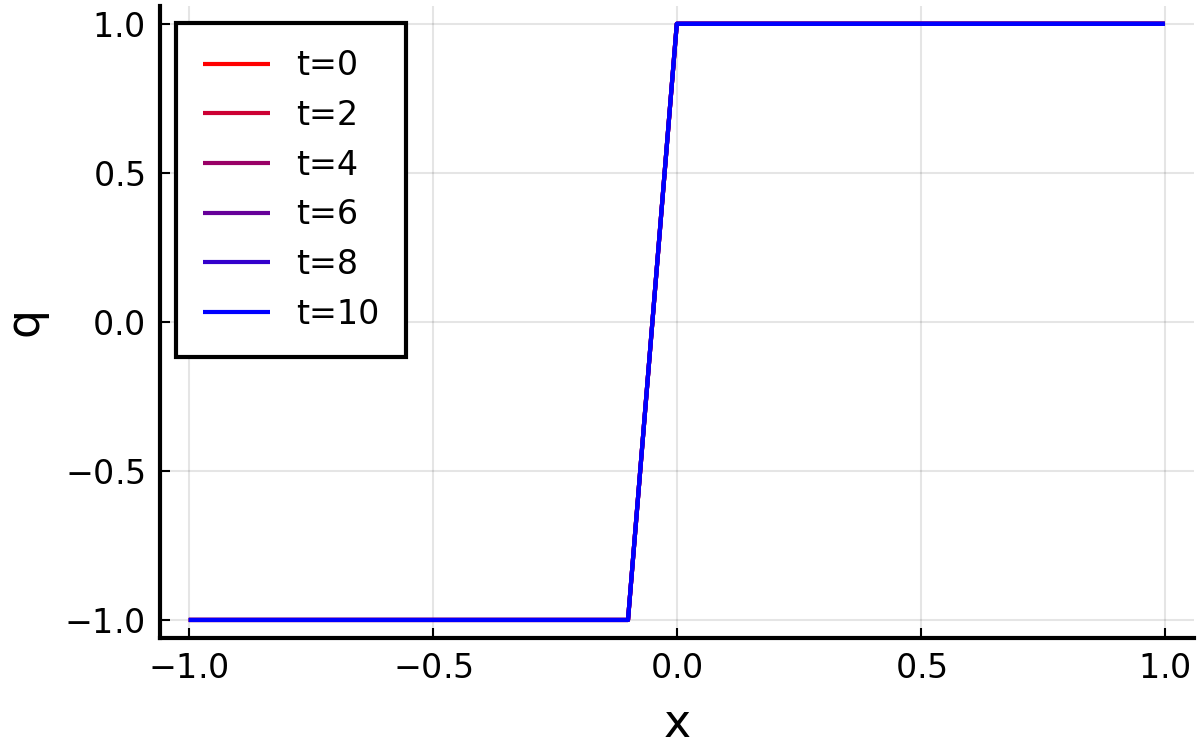
result

Godunov法


Godunov法を使って, ケース4を計算する. 新たに以下の数値流束を定義.

Julia 

function GODUNOV(q, Δt, Δx, j)
    qm = 0.5 * (q[j] + abs(q[j]))
    qp = 0.5 * (q[j+1] - abs(q[j+1]))
    return max(0.5*qm^2, 0.5*qp^2)
end

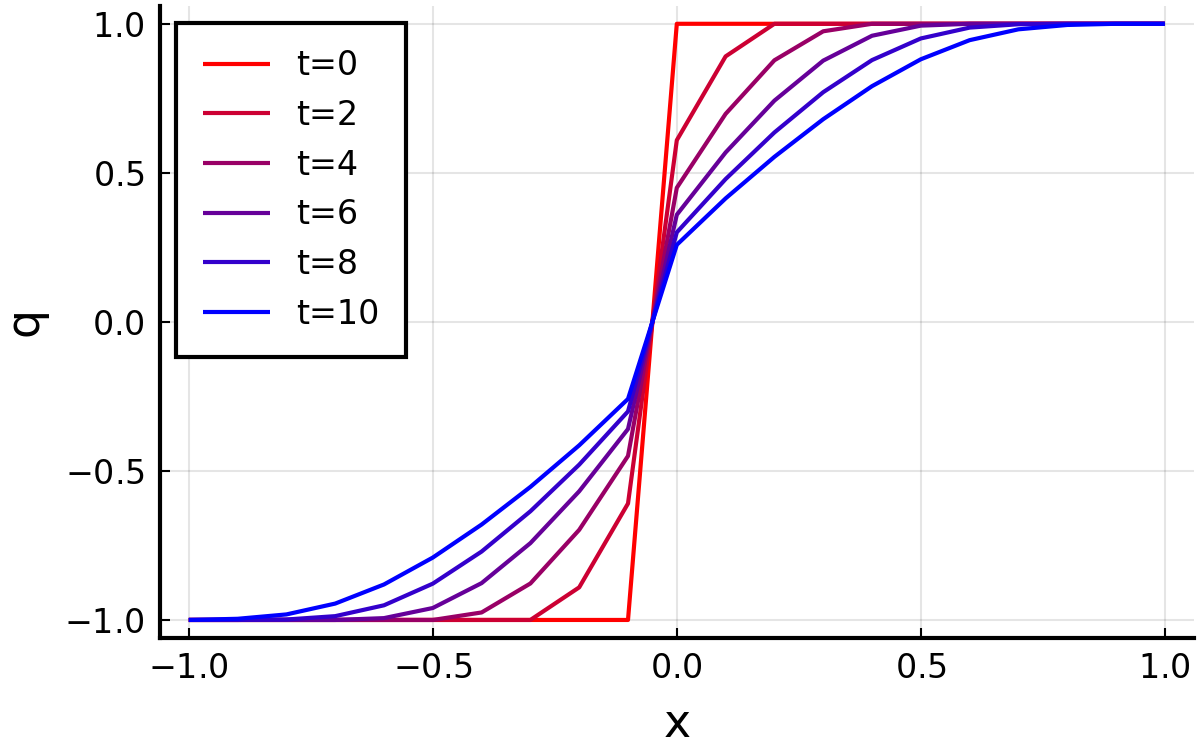
計算結果.

不連続がひろがっていく様子がわかる. これは, 物理的にも正しい現象である ( ということが解説されている ) . 前節のケース4の結果は, 数学的には正しいが, 物理的に実現する 現象ではない.

result
コード(click) Julia 

q1   = -1.0;
q2   = 1.0;
Δt   = 0.05;
Δx   = 0.1;
nmax = 21;
jmax = 21;

x, q = init(q1, q2, Δx, jmax)
res  = do_computing(x, q, Δt, Δx, nmax, GODUNOV)

# 図示
pyplot(fmt=:svg, size=(400, 250))
plot(x, res[:, 1:2:11],
     labels=["t=0" "t=2" "t=4" "t=6" "t=8" "t=10"],
     color_palette=palette([:red, :blue], 6))
xlabel!("x")
ylabel!("q")
PyPlot.savefig("img/2_6_godunov.png", dpi=300)

この記事のTOP    BACK    TOP