『pythonで学ぶ流体力学の数値計算法』 Chapter 2-4をJuliaで
最終更新:2020/11/21
『pythonで学ぶ流体力学の数値計算法』 Chapter 2-4のコードを, 練習を兼ねてJuliaで書いてみました. 詳細なことを書くと著作権的にだめな気もするので, 詳しい解説などはありません.
Julia Version 1.5.0
各手法の数値流束函数を定義
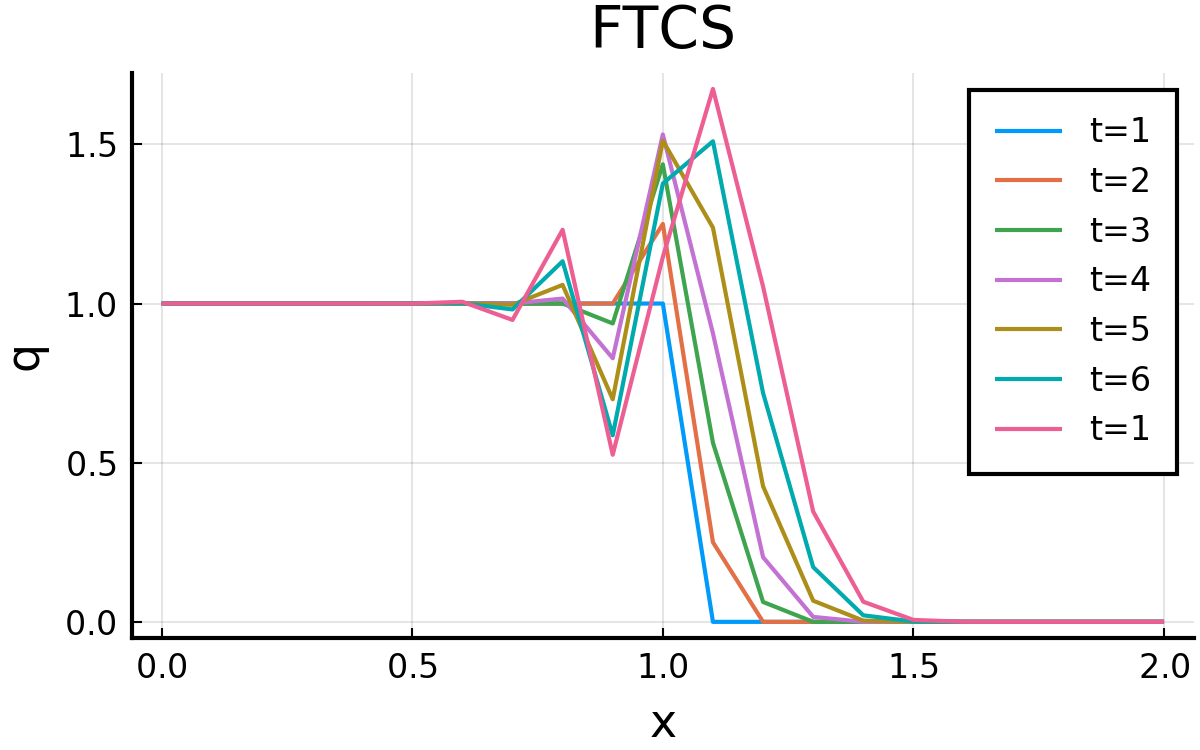
FTCS, 一次精度風上差分, LAX法, Lax-Wendroff法を, 数値流束の考え方を活用したプログラム化する. それぞれの計算結果を示し, Chapter2−2の結果と同じになることを確認する.
以下に, 各手法の数値流束函数を定義する.
FTCS
\begin{align}
\tilde{f}_{j+1/2}^{\,n} =c \cdot \frac{q_{j+1}^{n}+q_{j}^{\,n}}{2}
\end{align}
Julia
function FTCS(q, c, Δt, Δx, j)
0.5 * c * (q[j+1] + q[j])
end
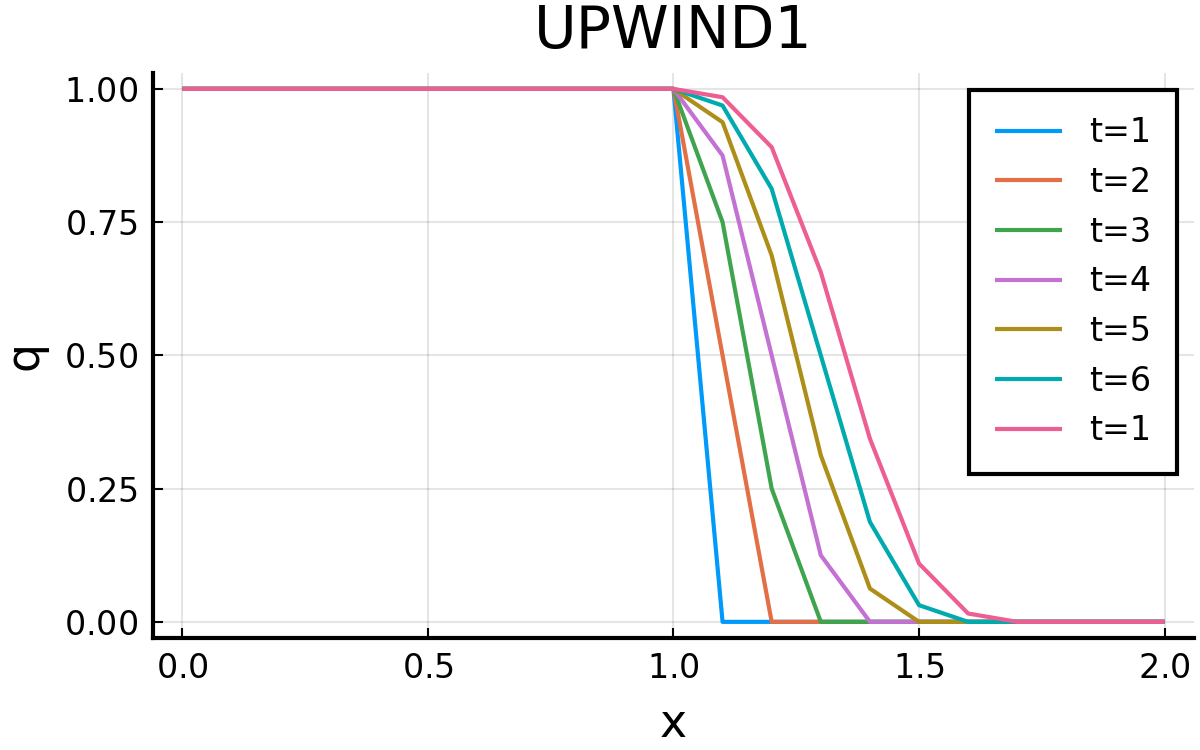
一次精度風上差分
\begin{align}
\tilde{f}_{j+1/2}^{\,n} = c \cdot q_{j}^{\,n}
\end{align}
Julia
function UPWIND1(q, c, Δt, Δx, j) c * q[j] end
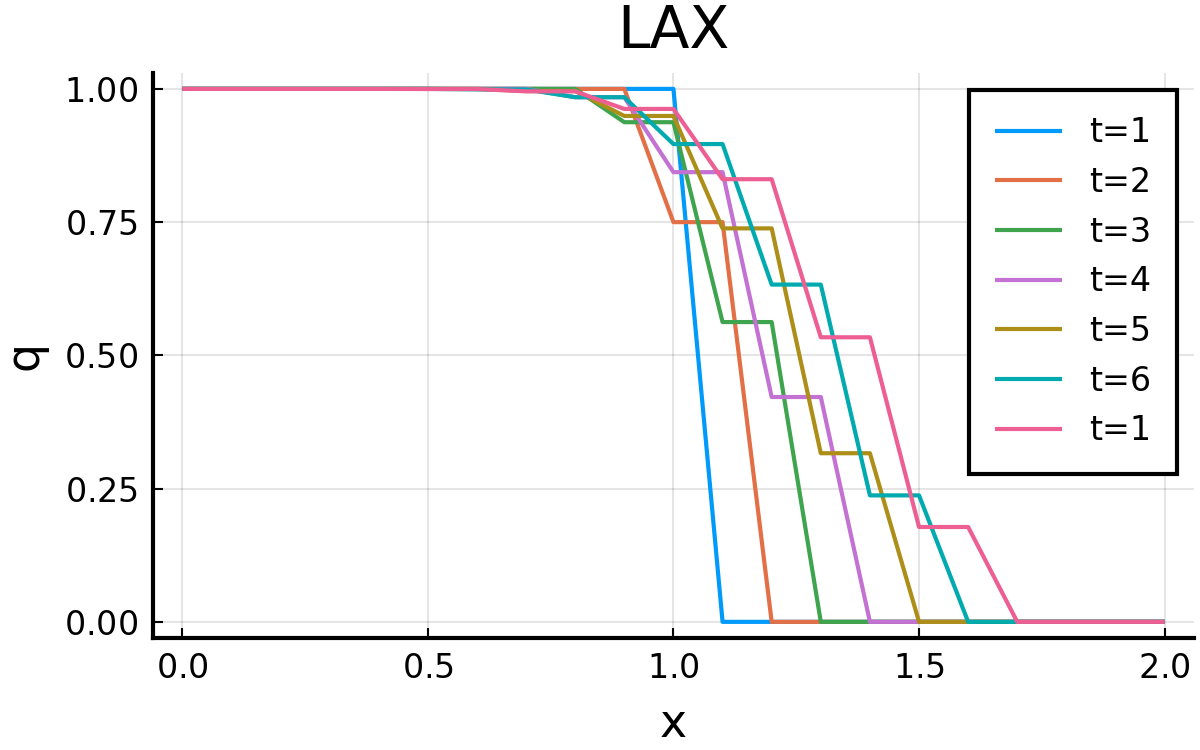
LAX法
\begin{align}
\tilde{f}_{j+1/2}^{\,n}
= \frac{c}{2}
\left[
\left(1 - \frac{1}{\nu}\right) q_{j+1}^{\,n}+
\left(1 + \frac{1}{\nu}\right) q_{j}^{\,n}
\right]
\end{align}
where,
\begin{align}
\nu = c \frac{\Delta t}{\Delta x}
\end{align}
Julia
function LAX(q, c, Δt, Δx, j)
ν2 = 1/(c*Δt/Δx)
0.5 * c * ((1-ν2)*q[j+1] + (1+ν2)*q[j])
end
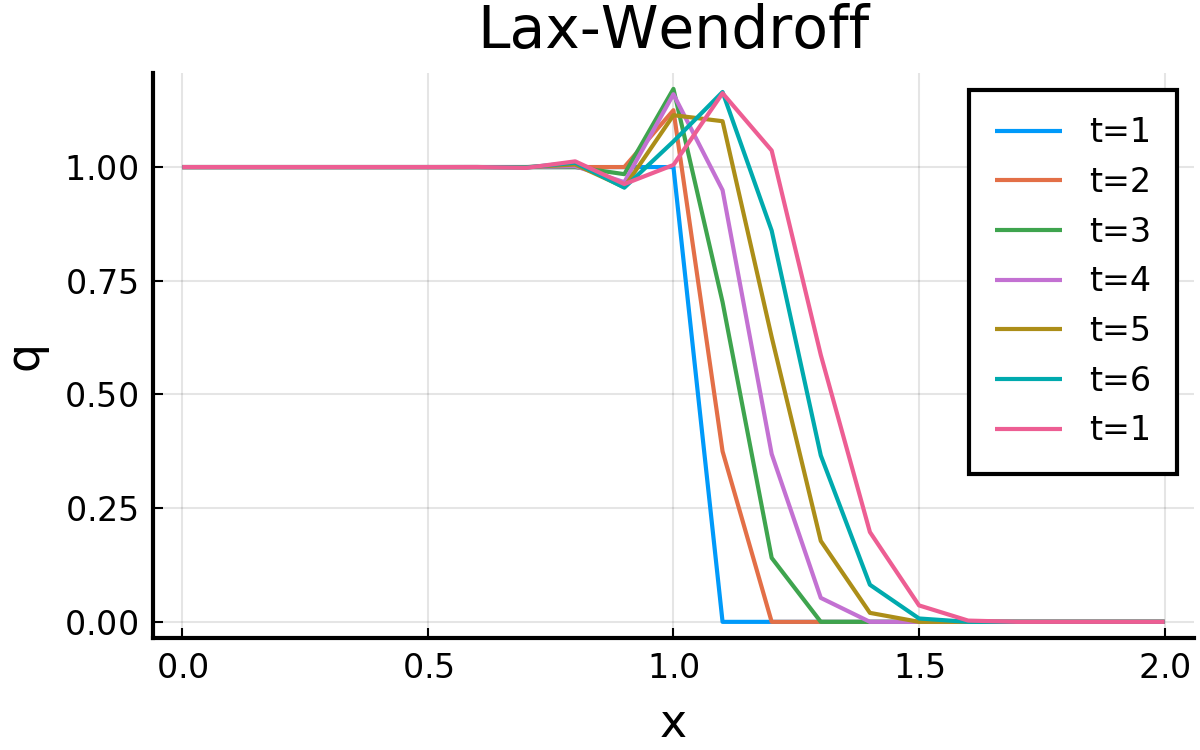
Lax-Wendroff法
\begin{align}
\tilde{f}_{j+1/2}^{\,n}
= \frac{1}{2}
\left[
c\left(1 - \nu\right) q_{j+1}^{\,n}+
c\left(1 +\nu\right) q_{j}^{\,n}
\right]
\end{align}
Julia
function LAXWEN(q, c, Δt, Δx, j)
ν = c*Δt/Δx
0.5 * c * ((1-ν)*q[j+1] + (1+ν)*q[j])
end
メインパートのプログラム
輸送速度, 時間, 空間方向の刻み幅を格納する構造体.
Julia
struct Params
c::Float64
Δt::Float64
Δx::Float64
end
メインプログラム. 上記構造体と数値流束函数 ( ff ) を引数にもつ.
以下で示される式を解く. (教科書式(2.25))
\begin{align}
q_{j}^{n+1} =
q_{j}^{n} - \frac{\Delta t}{\Delta x}
(\tilde{f}_{j+1/2}^{\,n} - \tilde{f}_{j-1/2}^{\,n})
\end{align}
Julia
function main(p, ff)
jmax = 21 # 空間 ( x方向 ) 刻み
nmax = 6 # 時間刻み
x = collect(range(0, p.Δx*(jmax-1), length=jmax))
q = zeros(Float64, jmax)
qs = zeros(Float64, jmax, nmax+1) #結果を格納する変数
# init
if p.c>0
q[1:div(jmax, 2)+1] .= 1.0 #前半分を0にする
else
q[div(jmax, 2)+1:end] .= 1.0 #後半分を0にする
end
qs[:, 1] = q
for n in 1:nmax
qold = q[:]
for j in 2:jmax-1
ff1 = ff(qold, p.c, p.Δt, p.Δx, j)
ff2 = ff(qold, p.c, p.Δt, p.Δx, j-1)
q[j] = qold[j] - (ff1-ff2)*p.Δt/p.Δx
end
qs[:, n+1] .= q
end
return x, qs
end
実行
以上の函数たちを用いて, 例えばFTCSなら以下のようにして実行できる.
Julia
p = Params(1.0, 0.05, 0.1) x, qs = main(p, FTCS)
こうして求めた結果が以下. Chapter2−2の結果と一緒になっているとおもう. ( それぞれ7本目がt=1となっているのはミス )