『pythonで学ぶ流体力学の数値計算法』 Chapter 2-3をJuliaで
最終更新:2020/11/21
『pythonで学ぶ流体力学の数値計算法』 Chapter 2-3のコードを, 練習を兼ねてJuliaで書いてみました. 詳細なことを書くと著作権的にだめな気もするので, 詳しい解説などはありません.
Julia Version 1.5.0
輸送速度符号が不明な線形問題
以下の移流方程式を離散化してとく.
\begin{align}
\frac{\partial q}{\partial t} + c\frac{\partial q}{\partial x} = 0\:(\color{red} {c>0とは限らない})
\end{align}
今, 以下のように\( c \)の符号によって場合わけした風上差分を行なう.
\begin{align}
q^{n+1}_{j} =
q^{n}_{j} - c \frac{\Delta t}{\Delta x}
(q^{n}_{j} - q^{n}_{j-1}) \qquad(c\geq0)
\\
q^{n+1}_{j} =
q^{n}_{j} - c \frac{\Delta t}{\Delta x}
(q^{n}_{j+1} - q^{n}_{j}) \qquad(c\lt0)
\end{align}
これを一式で表す.
\begin{align}
q^{n+1}_{j}
= q^{n}_{j} -
\Delta t
\left(
\frac{c+|c|}{2}\cdot \frac{q^{n}_{j}-q^{n}_{j-1}}{\Delta x}+
\frac{c-|c|}{2}\cdot \frac{q^{n}_{j+1}-q^{n}_{j}}{\Delta x}
\right)
\end{align}
以下では, 教科書に則って, 輸送速度が正ならば前半分が1.0 ( ほかは0.0 ) の初期状態, 負ならば後半分に1.0 ( ほかは0.0 ) の初期状態を与えている.
Julia
# 変数
struct Params
c::Float64
Δt::Float64
Δx::Float64
end
# メイン関数
function main(p)
jmax = 21 # 空間 ( x方向 ) 刻み
nmax = 6 # 時間刻み
x = collect(range(0, p.Δx*(jmax-1), length=jmax))
q = zeros(Float64, jmax)
qs = zeros(Float64, jmax, nmax+1) #結果を格納する変数
# init
if p.c>0
q[1:div(jmax, 2)+1] .= 1.0 #前半分を0にする
else
q[div(jmax, 2)+1:end] .= 1.0 #後半分を0にする
end
qs[:, 1] = q
temp1 = p.Δt*(p.c+abs(p.c))/(2*p.Δx) #FOR文の中で使う定数を事前に計算
temp2 = p.Δt*(p.c-abs(p.c))/(2*p.Δx) #FOR文の中で使う定数を事前に計算
for n in 1:nmax
qold = q[:]
for j in 2:jmax-1
q[j] = qold[j] - (temp1*(qold[j]-qold[j-1]) + temp2*(qold[j+1]-qold[j]))
end
qs[:, n+1] .= q
end
return x, qs
end
結果. 無事, \( c = 1.0 \)と\( c = -1.0 \)双方で計算ができた.
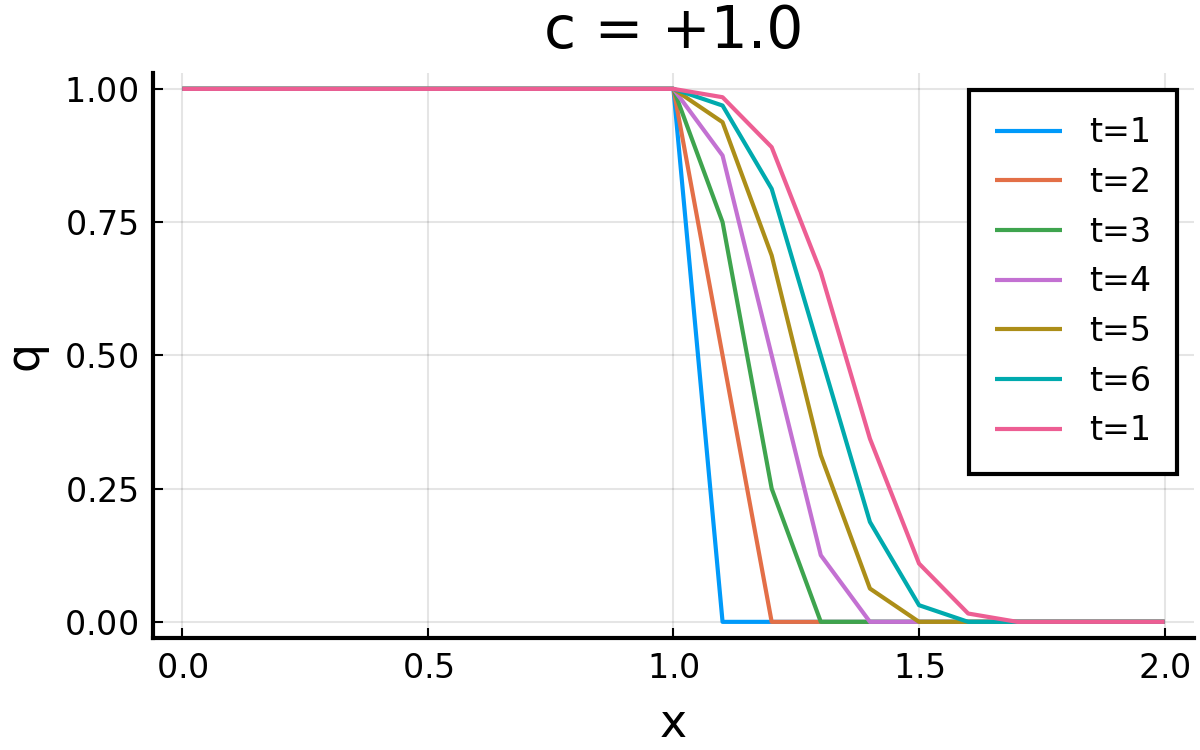
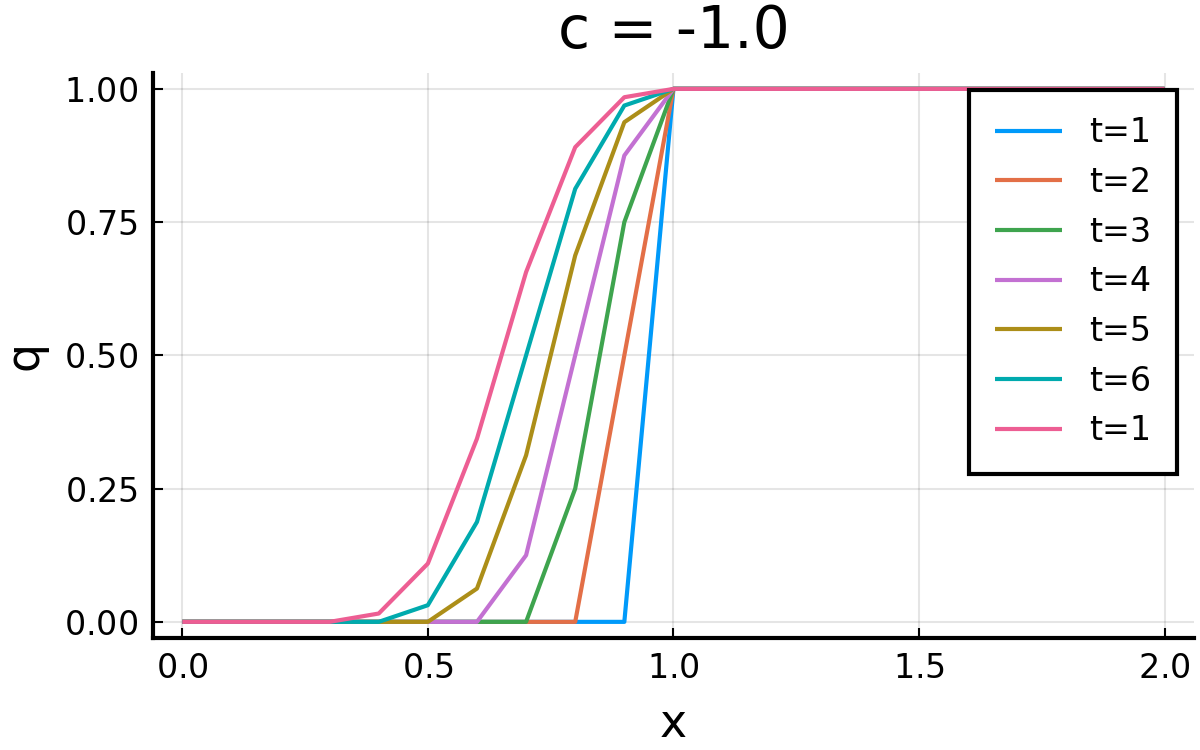
コード(click)
Julia
using Plots
# 実行 ( cは正 )
p = Params(+1.0, 0.05, 0.1)
x, qs = main(p)
# 図示
pyplot(fmt=:svg, size=(400, 250))
plot(x, qs, labels=["t=1" "t=2" "t=3" "t=4" "t=5" "t=6"])
xlabel!("x")
ylabel!("q")
title!("c = +1.0")
PyPlot.savefig("img/2_3_pos.png", dpi=300)
# 実行 ( cは負 )
p = Params(-1.0, 0.05, 0.1)
x, qs = main(p)
# 図示
pyplot(fmt=:svg, size=(400, 250))
plot(x, qs, labels=["t=1" "t=2" "t=3" "t=4" "t=5" "t=6"])
xlabel!("x")
ylabel!("q")
title!("c = -1.0")
PyPlot.savefig("img/2_3_neg.png", dpi=300)