『pythonで学ぶ流体力学の数値計算法』 Chapter 2-2をJuliaで

最終更新：2020/11/21

『pythonで学ぶ流体力学の数値計算法』 Chapter 2-2のコードを, 練習を兼ねてJuliaで書いてみました. 詳細なことを書くと著作権的にだめな気もするので, 詳しい解説などはありません.

Julia Version 1.5.0

2.2(2) FTCS法


以下の移流方程式を離散化してとく.

\begin{align} \frac{\partial q}{\partial t} + c\frac{\partial q}{\partial x} = 0\:(c>0) \end{align}
\begin{align} \mathrm{I.C.}\left\{\begin{matrix} q = 1.0\, (x \leq 1.0) \notag \\ \phantom{qq = } 0.0\, (x > 1.0) \notag \end{matrix}\right. \end{align}

今, 時間方向 ( \(x\) ) に前進差分, 空間方向 ( \(t\) ) に中心差分を用いる.

\begin{align} \frac{q^{n+1}_{j} - q^{n}_{j}}{\Delta t} + c \frac{q^{n}_{j+1} - q^{n}_{j-1}}{2 \Delta x} = 0 \end{align}
これを\( q^{n+1}_{j} \)について解いてく.
\begin{align} q^{n+1}_{j} = q^{n}_{j} - \frac{c \Delta t}{2 \Delta x} (q^{n}_{j+1}-q^{n}_{j-1}) \end{align}

Julia 

# 変数
struct Params
    c::Float64
    Δt::Float64
    Δx::Float64
end
p = Params(1.0, 0.05, 0.1)

# メイン関数
function main(p)

    jmax = 21 # 空間 ( x方向 ) 刻み
    nmax = 6  # 時間刻み

    x = collect(range(0, p.Δx*(jmax-1), length=jmax))
    q = zeros(Float64, jmax)
    qs = zeros(Float64, jmax, nmax+1) #結果を格納する変数

    # init
    q[1:div(jmax, 2)+1] .= 1.0 #前半分を0にする
    qs[:, 1] = q

    temp = p.Δt*p.c/(2*p.Δx) #FOR文の中で使う定数を事前に計算
    for n in 1:nmax
        qold = q[:]
        for j in 2:jmax-1
            q[j] = qold[j] - temp*(qold[j+1]-qold[j-1])
        end
        qs[:, n+1] .= q
    end

    return x, qs
end

# 実行
x, qs = main(p);

# 図示
using Plots
pyplot(fmt=:svg, size=(400, 250))
plot(x, qs, labels=["t=1" "t=2" "t=3" "t=4" "t=5" "t=6"])
xlabel!("x")
ylabel!("q")
PyPlot.savefig("img/2_2_1.png", dpi=300)

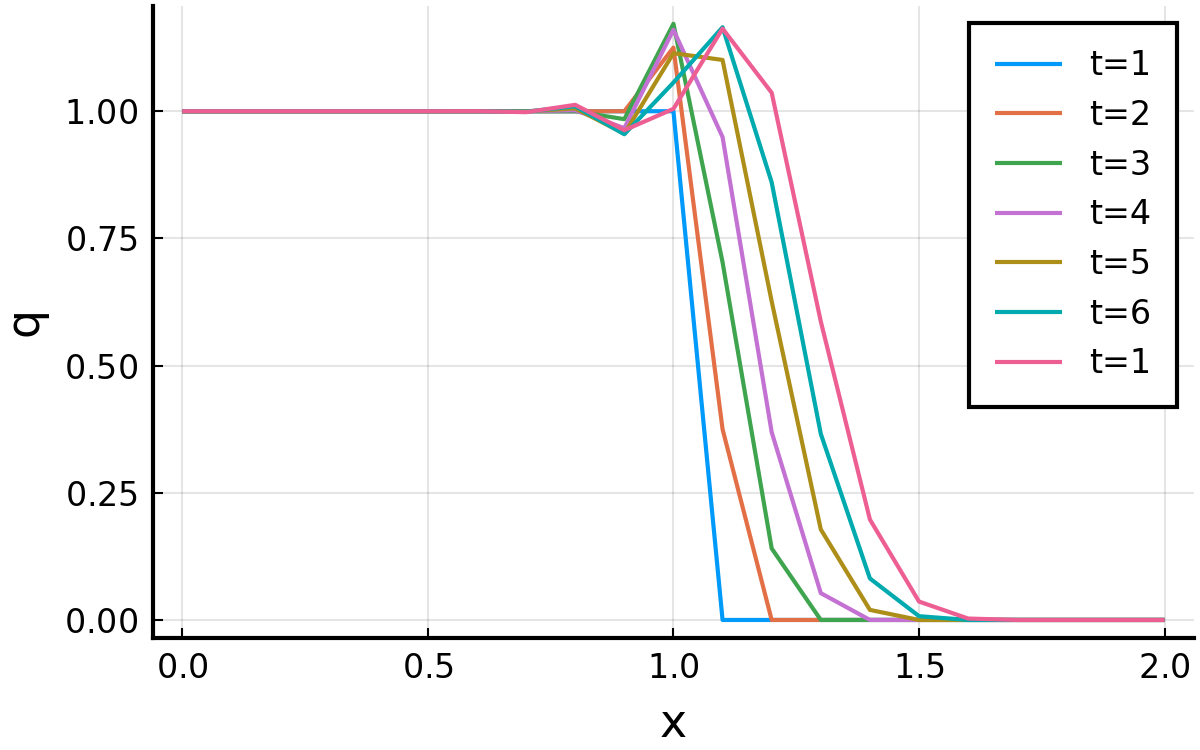
結果. 初期状態がそのまま流れていってほしいが, 振動している.

name

恥ずかしながら, qold = q[:]のところを, qold = qとしていたせいで, おかしな結果になり修正に大いに時間を使った. ココ にわかりやすい說明があるが, メモリアドレスのコピーを行っていたよう. MATLABしか使ってこなかったのであまり意識することのない現象であった.

2.2(3) 1st order UPWIND法


今度は, 空間方向に後退差分を使ってみる.

\begin{align} \frac{q^{n+1}_{j} - q^{n}_{j}}{\Delta t} + c \frac{q^{n}_{j} - q^{n}_{j-1}}{\Delta x} = 0 \end{align}
これを\( q^{n+1}_{j} \)について解く.
\begin{align} q^{n+1}_{j} = q^{n}_{j} - \frac{c \Delta t}{\Delta x} (q^{n}_{j}-q^{n}_{j-1}) \end{align}

FTCS法と比べて, for文まわりが以下のように変わるだけ.

Julia 

temp = p.Δt*p.c/p.Δx #FOR文の中で使う定数を事前に計算
for n in 1:nmax
    qold = q[:]
    for j in 2:jmax-1
        q[j] = qold[j] - temp*(qold[j]-qold[j-1])
    end
    qs[:, n+1] .= q
end

回してみます.

Julia 

# 実行
p = Params(1.0, 0.1, 0.1)
x, qs = main(p)

# 図示
pyplot(fmt=:svg, size=(400, 250))
plot(x, qs, labels=["t=1" "t=2" "t=3" "t=4" "t=5" "t=6"])
xlabel!("x")
ylabel!("q")
PyPlot.savefig("img/2_2_1.png", dpi=300)
name

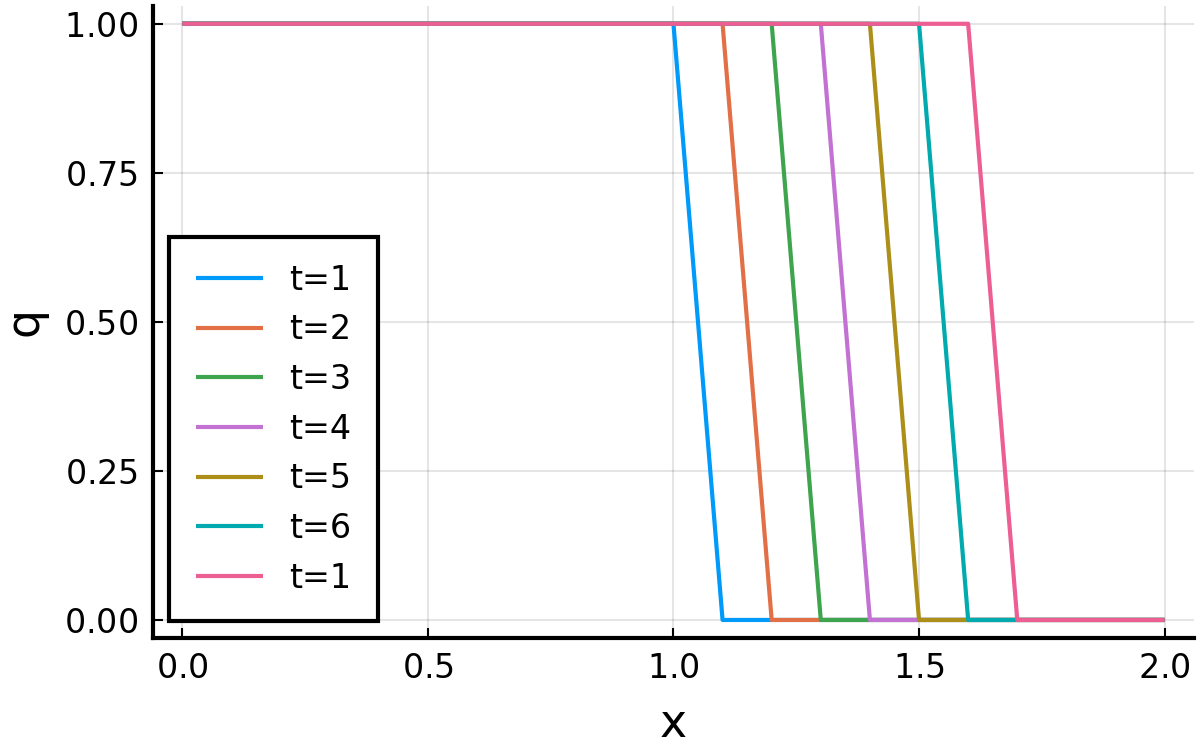
感動です. 今, \( c=1.0, \Delta t = 0.1, \Delta x = 0.1 \) なので, クーラン数は1.0.

2.2(4) 1st order DOWNWIND法


今度は, 一次精度風下差分を空間微分項に適用.

\begin{align} \frac{q^{n+1}_{j} - q^{n}_{j}}{\Delta t} + c \frac{q^{n}_{j+1} - q^{n}_{j}}{\Delta x} = 0 \end{align}
これを\( q^{n+1}_{j} \)について解く.
\begin{align} q^{n+1}_{j} = q^{n}_{j} - \frac{c \Delta t}{\Delta x} (q^{n}_{j+1}-q^{n}_{j}) \end{align}

for文まわりを以下のように変える.

Julia 

temp = p.Δt*p.c/p.Δx #FOR文の中で使う定数を事前に計算
for n in 1:nmax
    qold = q[:]
    for j in 2:jmax-1
        q[j] = qold[j] - temp*(qold[j+1]-qold[j])
    end
    qs[:, n+1] .= q
end
name

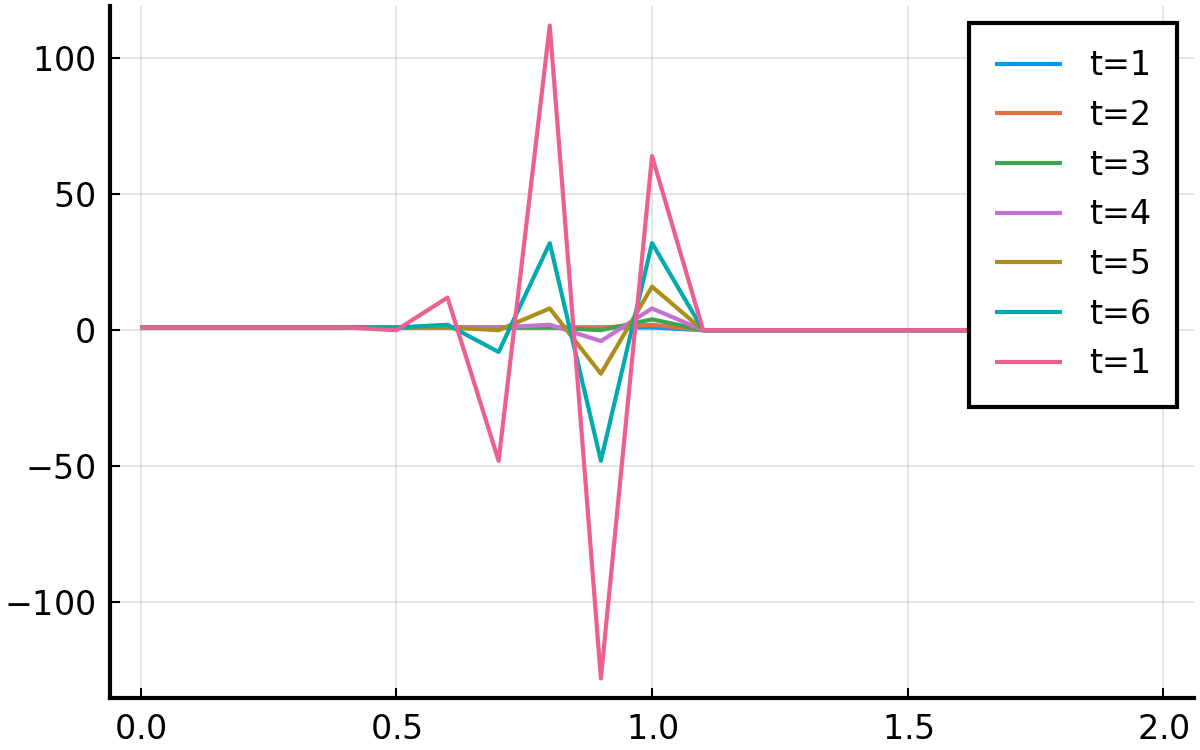
確かに全然だめ. この例では, \( c=1.0, \Delta t = 0.1, \Delta x = 0.1 \) .

ためしに, \( c=1.0, \Delta t = 0.01, \Delta x = 0.1 \) とした結果が以下. やはり, 計算が始まるが否や崩壊している.

name

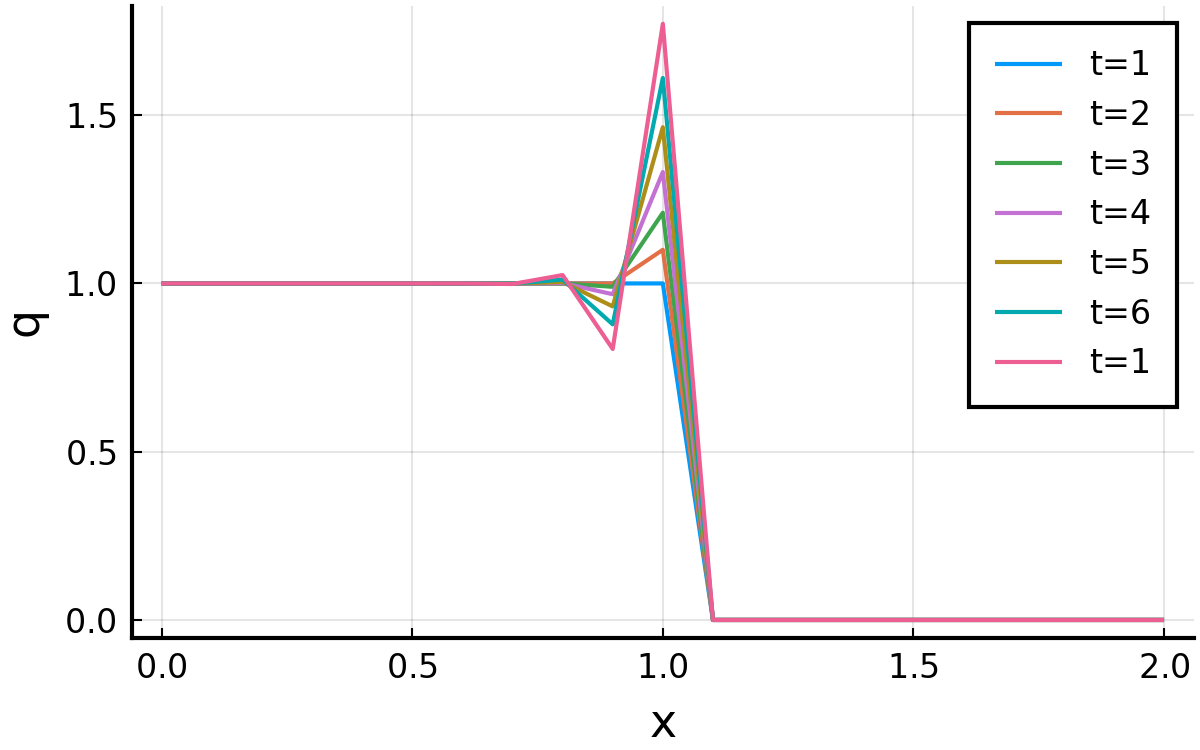
2.2(4) Lax法


Lax法は以下で示される.

\begin{align} q^{n+1}_{j} = \frac{1}{2}(q^{n}_{j+1}+q^{n}_{j-1}) - \frac{c \Delta t}{2 \Delta x}(q^{n}_{j+1}-q^{n}_{j-1}) \end{align}

for文まわりを以下のように変えて, \( c=1.0, \Delta t = 0.05, \Delta x = 0.1 \) で 計算してみる.

Julia 

temp = p.Δt*p.c/(2*p.Δx) #FOR文の中で使う定数を事前に計算
for n in 1:nmax
    qold = q[:]
    for j in 2:jmax-1
        q[j] = 0.5*(qold[j+1]+qold[j-1]) - temp*(qold[j+1]-qold[j-1])
    end
    qs[:, n+1] .= q
end
name

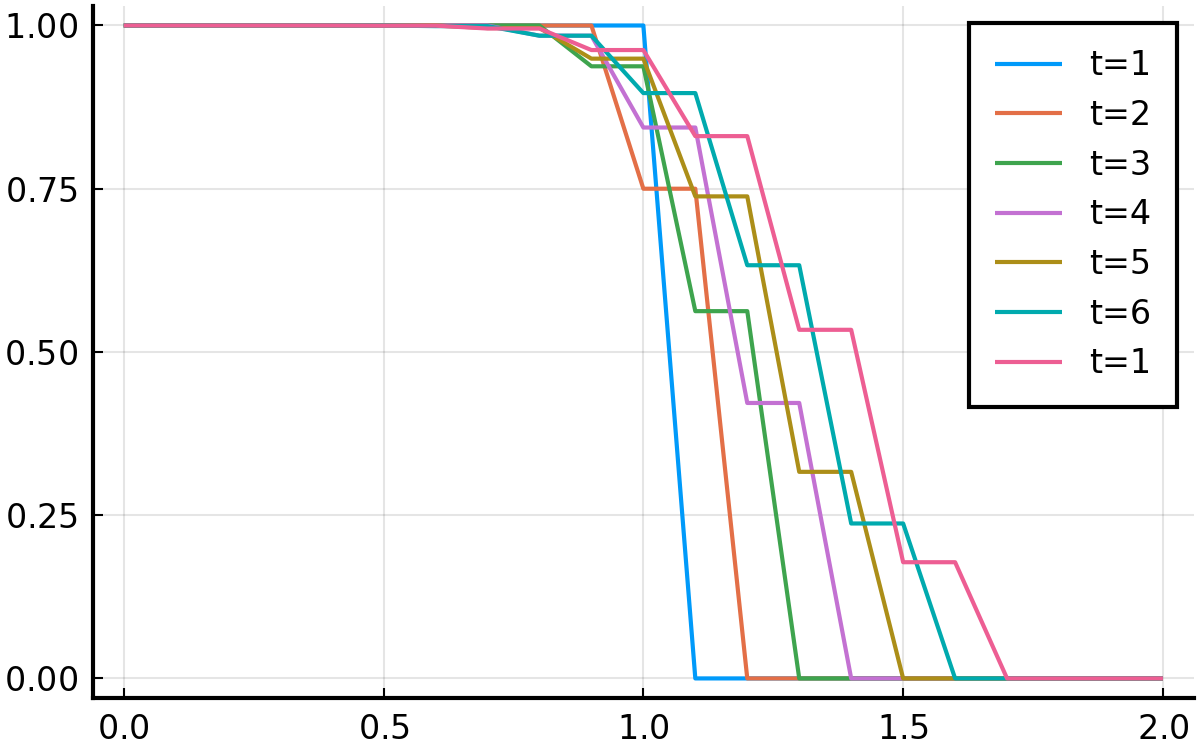
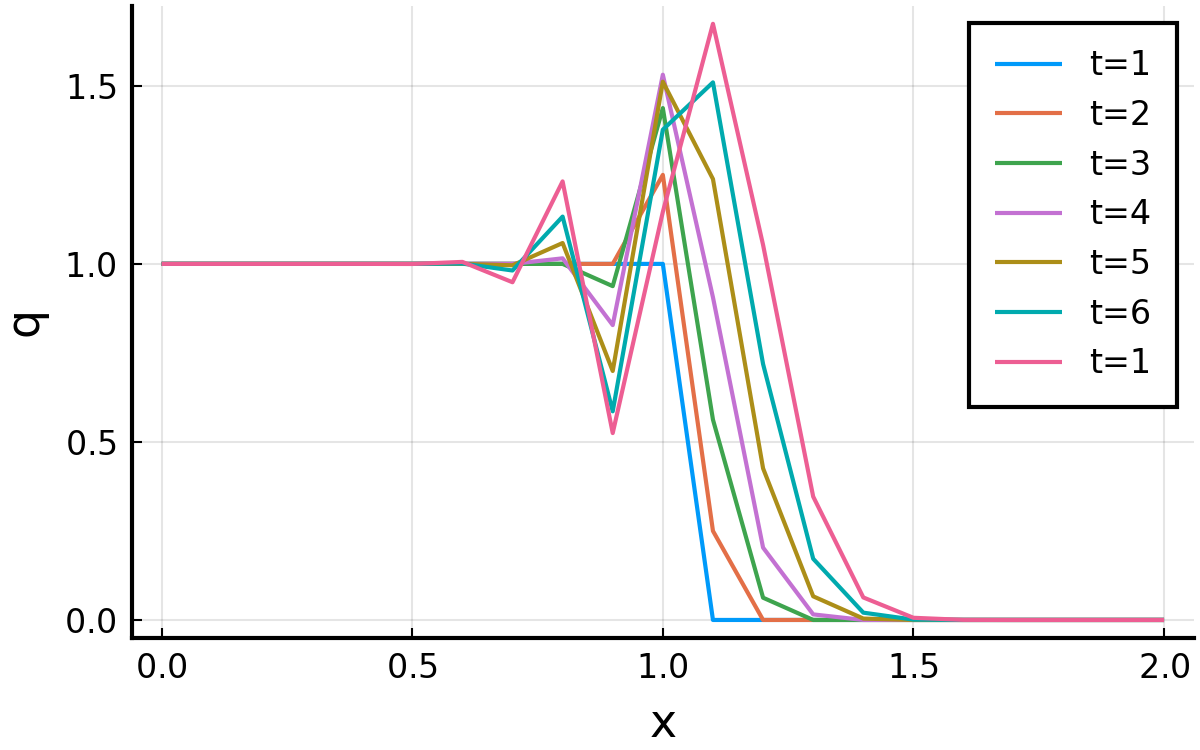
ついでに, \( c=1.0, \Delta t = 0.2, \Delta x = 0.1 \)とすることで, クーラン数を2.0にしてみる. もちろん崩れる.

name

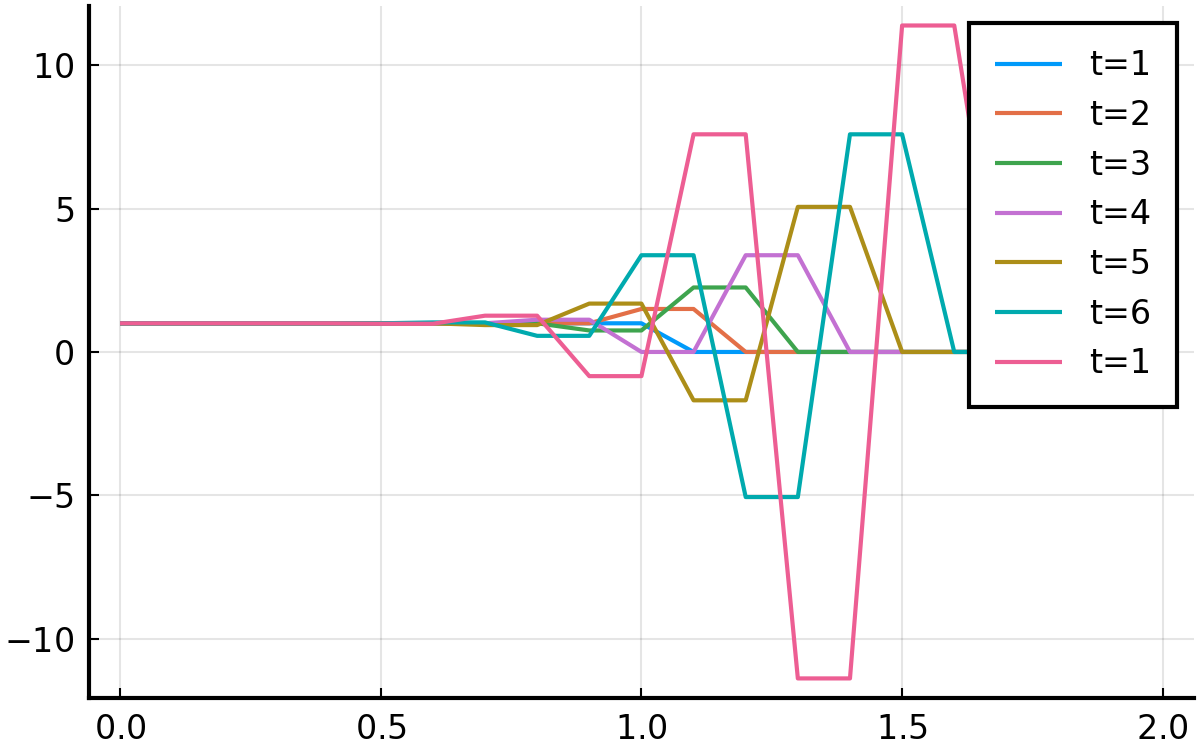
2.2(4) Lax-Wendroff法


Lax-Wendroff法は以下で示される.

\begin{align} q^{n+1}_{j} = q^{n}_{j} - \frac{c \Delta t}{2 \Delta x}(q^{n}_{j+1}-q^{n}_{j-1}) + \frac{c^2}{2}\left(\frac{\Delta t}{\Delta x}\right)^2(q^{n}_{j+1}-2q^{n}_{j} +q^{n}_{j-1}) \end{align}

for文まわりを以下のように変えて, \( c=1.0, \Delta t = 0.05, \Delta x = 0.1 \) で 計算してみる.

Julia 

temp1 = p.Δt*p.c/(2*p.Δx) #FOR文の中で使う定数を事前に計算
temp2 = 0.5*(p.Δt*p.c/p.Δx)^2 #FOR文の中で使う定数を事前に計算
for n in 1:nmax
    qold = q[:]
    for j in 2:jmax-1
        q[j] = qold[j] - temp1*(qold[j+1]-qold[j-1]) + temp2*(qold[j+1]-2*qold[j]+qold[j-1])
    end
    qs[:, n+1] .= q
end
name

この記事のTOP    BACK    TOP