伊藤『確率論』定理2.6の証明

最終更新：2021/10/31

伊藤『確率論』定理2.6の証明を詳細に追ってみる.

非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

定義

強同型

$(\Omega_1, P_1)$, $(\Omega_2, P_2)$ を確率空間とする. このとき, 全単射 $f:\Omega_1 \longrightarrow \Omega_2$ が

\begin{align}\large{ A_1 \in \cD(P_1) \Longleftrightarrow f(A_1) \in \cD(P_2) \Longrightarrow P_1(A_1) = P_2(f(A_1)) }\end{align}

をみたすとき, $f$ を$(\Omega_1, P_1)$ から $(\Omega_2, P_2)$ への強同型写像という. また, $(\Omega_1, P_1)$, $(\Omega_2, P_2)$ は強同型といい, $(\Omega_1, P_1) \approx (\Omega_2, P_2)$ と記す. 写像を明示するときは, $(\Omega_1, P_1) \approx (\Omega_2, P_2) \; (f)$ などと記す. なお, 強同型は同値関係である.

制限

確率空間 $(\Omega, P)$ の $P$ 測度 $1$ の部分集合 $\Omega^{\prime}$ をとり, $P$ の $\Omega^{\prime}$ への制限 $P' = P|_{\Omega'}$を以下で定義する.

\begin{align} \large \cD(P') &\large= \{ A' \in \cD(P) \mid A' \subset \Omega' \}, \\[5pt] \large P'(A') &\large= P(A'),\; A' \in \cD(P'). \notag \end{align}

同型

$(\Omega_i, P_i)$, $(i = 1, 2)$ の $P_i$ 測度 $1$ の部分集合 $\Omega_i^{\prime}$ が存在して, $(\Omega_1, P_1)$ の $\Omega_1^{\prime}$ への制限と, $(\Omega_2, P_2)$ の $\Omega_2^{\prime}$ への制限とが強同型であるとき, $(\Omega_1, P_1)$ と $(\Omega_2, P_2)$ とは同型であるといい, $(\Omega_1, P_1) \sim (\Omega_2, P_2)$ と記す. なお, 同型は同値関係である.

標準確率測度

$P$ を $\Omega$ 上の完備確率測度とする. $(\Omega, P) \sim (\mathbb{R}, \mu)$ であるとき, $(\Omega, P)$ を標準確率空間, $P$ を $\Omega$ 上の標準確率測度という. なお, $\mu$ は $\mathbb{R}$ 上の正則確率測度である.

像測度

$S$, $T$ を一般の集合とし, $P$ を $S$ 上の完備確率測度, $f:S \longrightarrow T$ を任意の写像とする. このとき, $T$ 上に集合函数 $Q$ を以下のように定義する.

\begin{align} \large \cD(Q) &\large= \{ B \subset T \mid f^{-1}(B) \in \cD(P) \}, \\[5pt] \large Q(B) &\large= P(f^{-1}(B)). \end{align}

このとき, $Q$ は $T$ 上の確率測度となり, $P$ の $f$ による像測度 $Pf^{-1}$, $fP$ とあらわす.

参考になるかわからないけど, $Q$ は以下の図の関係を満たすように, 集合 $T$ 上に定義されている.

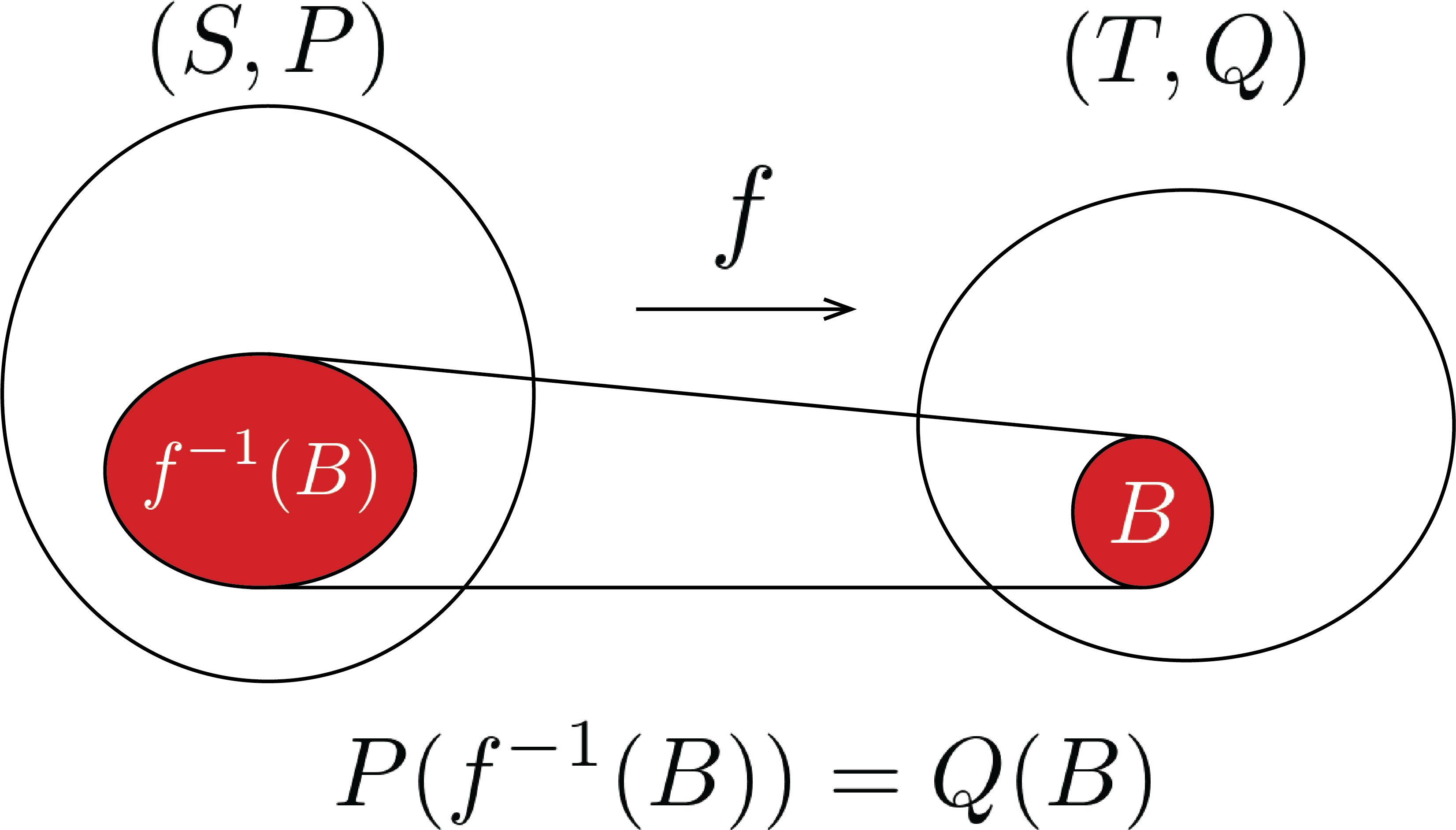
なお, $P$ が完備なら, $Q = Pf^{-1}$ も完備.

証明 ( click )

$Q(N) = 0$, $E \subset N$ で, $E$ は $Q$ 可測でないとする ( つまり, $Q(E) = 0$ が成り立たない ) . すると, $N \subset T$ なので $E \subset T$. よって $\cD(Q)$ の定義より,

\begin{align} f^{-1}(E) \notin \cD(P). \end{align}

しかしこれでは, $f^{-1}(N) \in \cD(P)$, $P(f^{-1}(N)) = 0$ なのに $f^{-1}(E) \subset f^{-1}(N)$ は $P$ 零でないことになり, $P$ の完備性に矛盾する.

$\blacksquare$

補題2.1

Statement

$P$ を完備可分距離空間 $S$ の上の正則確率測度とする. このとき, 任意の $A \in \cD(P)$, $\ve \gt 0$, に対しコンパクト集合 $K \subset A$ をとってきて, $P(A-K) \lt \ve$ とできる. この性質を $K$ 正則という.

証明

以下の順番で示す.

$A=S$ のとき, $A$ が $K$ 正則,
$A$ が一般のBorel集合のとき $A$ が $K$ 正則.

　 i 　 $A=S$ のとき
$S$ が可分 $\Rightarrow$ $S$ のなかに稠密な可算集合 $\{ a_1, a_2, \ldots \}$ がある. また, $S$ 上の距離を $\rho$ とする. 今,

\begin{align} B_{nk} = \left\{ x \in S \;\left|\; \rho(x, a_n) \leq \frac{1}{k} \right. \right\} \end{align}

とおけば, これは各 $a_n$ を中心とする半径 $1/k$ の閉球であり, $S$ は稠密なので $1/k$ がどれほど小さくても ( つまりあらゆる $k$ に対して )

\begin{align} \bigcup_{n=1}^\infty B_{nk} = S, \quad \mathrm{hence} \quad \bigcup_{n=1}^N B_{nk} \rightarrow S\; (N \rightarrow \infty) \end{align}

となる. よって各々の $k$ に対して十分大きな $N(k)$ がとれて,

\begin{align} P(S - B_k) \lt 2^{-(k+1)}\ve,\quad B_k = \bigcup_{n=1}^{N(k)} B_{nk} \end{align}

とできる. ここで, $2^{-(k+1)}\ve$ はどれだけ小さくてもいいので, この後の便宜上この値を選んでいる.

$B_k$ は閉球の合併なので閉, よって $K = \bigcap_{k=1}^\infty B_k$ も閉. また,

\begin{align} K \subset B_k = \bigcup_{n=1}^{N(k)} B_{nk}. \label{eq_i} \end{align}

$B_{nk}$ は直径 $2/k$ 以下の閉球ゆえ, $K$ は全有界. しかも, 仮定より $S$ は完備なので, 全有界かつ閉部分集合である $K$ はコンパクト ( cf: コンパクト $\Leftrightarrow$ 完備かつ全有界 ) .

さらに,

\begin{align} P(S-K) &= P \left( S - \bigcap_{k=1}^\infty B_k \right) \\[5pt] &= P\left( \bigcap_{k=1}^\infty (S-B_k) \right) \notag\\[5pt] &\leq \sum_{k=1}^\infty P(S-B_k) \lt \ve. \end{align}

　 ii 　 $A$ が一般のBorel集合のとき
方針としては, まず ${}^\forall \ve \gt 0$ に対して閉集合 $F \subset A$ と開集合 $G \supset A$ とがとれて,

\begin{align} P(G-F) \lt \ve \label{eq_ro} \end{align}

とできることを示す. そのためには, 上の性質をもつ $A$ の全体 $\cB$ が Borel集合族 $\cB(S)$ を含んでいれば十分.

ここで, まず $\cB$ が $S$ の開集合族を含む $\sigma$-加法族であることを使う.

証明 ( click )

$\sigma$-加法族の条件をひとつづつ確認していく. ただ, σ.1と開集合族を含むこととを併せて, σ.1'で示す.

　 σ.1' 　
第一に, $\cB$ は全ての開集合を含む. なぜなら, 距離空間では, 開集合は閉集合の可算和でいくらでも近似できるて, それは即ち\eqref{eq_ro}を成立させることができることを示す. よって, もちろん $S$ も $\cB$ に含まれる.

　 σ.2 　
$\cB$ の定義により, $A \in \cB \Rightarrow {}^\exists F, G,\; G \supset A \supset F$ なので, $A^c$ に対して, $G^c \subset A^c \subset F^c$. よって, $\cB$ は補演算で閉じている.

　 σ.3 　
$A_n \in \cB$, $(n = 1, 2, \ldots)$ のとき, 各$n$ に対して

\begin{align} F_n \subset A_n \subset G_n,\; P(G_n - F_n) \lt 2^{-n} \ve \end{align}

となる $F_n$, $G_n$がとれて, 当然

\begin{align} \bigcup_{n=1}^\infty F_n \subset \bigcup_{n=1}^\infty A_n \subset \bigcup_{n=1}^\infty G_n \end{align}

である. また,

\begin{align} P \left( \bigcup_{n=1}^\infty G_n - \bigcup_{n=1}^\infty F_n \right) \color{red}{\leq} \sum_{n=1}^\infty P(G_n - F_n) \lt \ve \end{align}

なので ( $\color{red}{\leq}$ は簡単な集合論の内容なので証明略 ) , $N$ を充分大きく取れば,

\begin{align} P \left( \bigcup_{n=1}^\infty G_n - \bigcup_{n=1}^N F_n \right) \lt \ve,\quad \bigcup_{n=1}^N F_n \subset \bigcup_{n=1}^\infty A_n \subset \bigcup_{n=1}^\infty G_n. \end{align}

$\bigcup_{n=1}^N F_n$ は閉, $\bigcup_{n=1}^\infty G_n$ は開より, $\bigcup_{n=1}^\infty A_n \in \cB$. よって, $\cB$ は, 可算和で閉じている.

$\square$

これが成り立つなら, 当然 $\cB \supset \cB(S)$ である ( $\cB(S)$ は全ての開集合を含む最小の $\sigma$-加法族であった ) . これで, 任意のBorel集合 $A$ が $K$ 正則であることを示す準備ができた.

いま, 任意のBorel集合 $A$, ${}^\forall \ve \gt 0$ に対して, ${}^\exists F \subset A$, $P(A-F) \lt \ve$. $P$ が正則 ( $\cD(P)$ が Borel集合族かつ完備 ) なので, これは任意の $P$ 可測集合に対して成立.

ここで, \eqref{eq_i}で定義したコンパクト集合 $K$ を使うと, $F$ は閉なので $F \cap K$ は $A$ のコンパクト集合で,

\begin{align} P(A - F \cap K) &\leq P(A-F) + P(A \setminus K) \\[5pt] &\lt \ve + \ve = 2 \ve \notag. \end{align}

$\ve$ は任意なので, $A$ が一般のBorel集合のときは $F \cap K$ というコンパクト集合をとってくることで, $A$ が $K$ 正則であると判る.

$\blacksquare$

補題2.2 ( Lusinの定理 )

Statement

$S$ : 完備可分距離空間,
$P$ : $S$ の上の正則確率測度,
$T$ : 可分距離空間,
$f: S \longrightarrow T$ を$P$ 可測 ( すなわち, 可測 $\cD(P)/\cB(T)$ ) とする.

このとき, 任意の $P$ 可測集合 $A \subset S$, ${}^\forall \ve \gt 0$ に対し, あるコンパクト集合 $K = K(A, \ve) \subset A$ をが存在し,

\begin{align}\large{ P(A-K) \lt \ve,\quad f_K := f|_K : K \longrightarrow T,\quad f_K \mathrm{\;is\;continuous}, }\end{align}

とできる.

証明

以下の順番で示す.

$P(A-K) \lt \ve$ なる $K$ の存在,
$f_K$ の連続性.

　 i 　 $P(A-K) \lt \ve$ なる $K$ の存在
$T$ 上の距離を $d_T$ とする. $T$ が可分であることより, 補題2.1 と同様に稠密な可算集合 $\{ b_1, b_2, \dots \} \subset T$ が取れて,

\begin{align} {}^\forall k \quad T = \bigcup_{n=1}^\infty B_{nk},\quad B_{nk} = \left\{ y \in T \;\left|\; d_T(y, b_n) \lt \frac{1}{k} \right. \right\}. \end{align}

今, $A_{nk} = A \cap f^{-1}(B_{nk})$ とするとこれは $P$ 可測. なぜなら, $B_{nk} \subset T$, $f$ が $\cD(P)/\cB(T)$ であることより, $f^{-1}(B_{nk}) \in \cD(P)$ で, $P$ 可測集合 ( これは $\sigma$-加法族 ) は $\cap$ 演算で閉じているから. さらに, $P$ 可測集合は差, 合併でも閉じているので, $A'_{nk} = A_{nk} \setminus \bigcup_{i \lt n} A_{ik}$ とすることで $P$ 可測かつ互いに素な $A'_{nk}$ が作れる. しかも,

\begin{align} A = A \cap S = A \cap f^{-1}(T) = \bigcup_{n=1}^\infty A \cap f^{-1}(B_{nk}) = \bigcup_{n=1}^\infty A_{nk} = \sum_{n=1}^\infty A'_{nk} \end{align}

となる.

いま, 補題2.1より, $A'_{nk} \in \cD(P)$ はコンパクト部分集合 $K_{nk} \subset A'_{nk}$ が取れて, $P(A'_{nk} - K_{nk}) \lt 2^{-n-k}$ とできる. したがって,

\begin{align} P\left(A - \sum_{n=1}^\infty K_{nk} \right) &= P \left( \sum_{n} A'_{nk} - \sum_{n} K_{nk} \right) \\[5pt] &\leq \sum_n P(A'_{nk} - K_{nk}) \notag \\[5pt] &\lt 2^{-k} \ve \notag \end{align}

となる.

$N(k)$ を十分に大きく取り, $K_k = \sum_{n=1}^{N(k)} K_{nk}$ とおくと, $K_K$ はコンパクト集合の有限和ゆえコンパクトで,

\begin{align} P(A - K_k) \lt 2^{-k} \ve. \label{eq221} \end{align}

さらに, $K = \bigcap_{k=1}^\infty K_k$ とおくとこれもコンパクトで,

\begin{align} P(A - K) \leq \sum_{k=1}^\infty P(A - K_k) \lt \ve. \end{align}

なぜなら,

\begin{align} P(A - K) &= P\left( A - \bigcap_{k=1}^\infty K_k \right) \\[5pt] &= P\left( A \cap \left( \bigcap_k K_k \right)^c \right) \notag \\[5pt] &= P\left( A \cap \bigcup_k K_k^c \right) \notag \\[5pt] &= P\left( \bigcup_k A \cap K_k^c \right) \notag \\[5pt] &= P\left( \bigcup_k (A - K_k) \right) \notag \\[5pt] &= \sum_{k=1}^\infty P(A - K_k). \notag \end{align}

これと, \eqref{eq221}からわかる.

$\square$

　 ii 　 $f_K$ の連続性
$K \subset K_k$ なので,

\begin{align} K = K \cap K_k = K \cap \sum_{n=1}^{N(k)} K_{nk} \color{#cf201f}{=} \sum_{n=1}^{N(k)} K \cap K_{nk}. \end{align}

なお, 等号 $\color{#cf201f}{=}$ は, $\sum$ が直和であることに注意すると普通の集合演算である. ここで, $K \cap K_{nk}$ の中に $\varnothing$ があれば, 和から外しておく. そして, 各 $K_{nk}$ の中から一つづつ $a_{nk}$ を任意にとり, これを固定して $g_k : K \longrightarrow T$ を

\begin{align} g_k(x) = f(a_{nk}),\; x \in K_{nk},\; n = 1, 2, \ldots , N(k) \end{align}

と定義する. $K_{nk} \subset A'_{nk}$ で $A'_{nk}$ は互いに素であったので, もちろん $K_{nk}$ も互いに素なコンパクト集合である. また, $g_k$ は $K_{nk}$ の上で一定値 $f(a_{nk})$ をとるので $g_k$ は連続. さらに, また, $x \in K \cap K_{nk}$ に対し,

\begin{align} f(a_{nk}), f(x) \in f(K_{nk}) \subset f(A_{nk}) \subset B_{nk} \end{align}

であるから,

\begin{align} d_T(g_k(x), f(x)) = d_T(f(a_{nk}), f(x)) \leq \frac{2}{k},\; n = 1, 2, \ldots , N(k). \end{align}

なおここで, $2/k$ は閉球 $B_{nk}$ の直径である.

よって, ${}^\forall x \in K$ に対し ( つまり, $f$ を $K$ に制限したとき )

\begin{align} d_T(g_k(x), f_K(x)) \lt \frac{2}{k}. \end{align}

$k$ は任意であったので, 左辺は $x$ に依存せず幾らでも小さくできる. つまり, $\{g_k\} \rightrightarrows f_K$ ( 一様収束 ) . また, $g_k$ は連続なので $f_K$ も連続だとわかる ( 参考:一様収束する函数列の連続性 ) .

$\square$

$\blacksquare$

補題2.3

Statement

$S$ : 完備可分距離空間,
$P$ : $S$ の上の正則確率測度,
$T$ : 可分距離空間,
$f: S \longrightarrow T$ を中への $P$ 可測 ( すなわち, 可測 $\cD(P)/\cB(T)$ ) 写像とする.

このとき, 像測度 $Q = Pf^{-1}$ は, $T$ 上の $K$ 正則確率測度.

証明

像測度の定義で記したように, $P$ は正則, すなわち完備なので $Q = Pf^{-1}$ も完備.

$A \in \cB(T)$ なら, $Pf^{-1}(A) \in \cD(P)$ ( これは可測 $\cD(P)/\cB(T)$ の定義そのもの ) , よって $P(f^{-1}(A)) = Q(A)$ が定義できるので, $A \in \cD(Q)$. すなわち, $\cD(Q) \supset \cB(T)$ ( これは, $K$ 正則であるための必要条件 ) .

これで, あとは「 $B \in \cD(Q)$ と ${}^\forall \ve \gt 0$ に対して, あるコンパクト集合 $K \subset B$ をとって $Q(B-K) \lt \ve$ とできる」ことを示せば証明は終わる.

$B \in \cD(Q)$ とすれば, $A = f^{-1}(B)$ が ( $f$ が $P$ 可測より ) $P$ 可測なので, 補題2.2より, あるコンパクト集合 $H \subset A$ をとってきて,

\begin{align} P(A-H) \lt \ve,\quad f_H := f|_H: H \longrightarrow T,\quad f_H \mathrm{\; is \; continuous} \end{align}

とできる. コンパクト集合の連続函数による像はコンパクトなので, $K = f_H(H) = f(H)$ はコンパクト. 集合論でよく知られたように, $f^{-1}(K) \supset H$ なので,

\begin{align} Q(B-K) = P(f^{-1}(B-K)) = P(f^{-1}(B) - f^{-1}(K)) \leq P(A-H) \lt \ve. \end{align}

$\blacksquare$

定理2.6

完備可分距離空間 $S$ の上の正則確率測度 $P$ は標準.

証明

補題2.1で使った集合 $B_{nk}$, $n, k = 1, 2, \dots$ を活用する. これらを一列に並べて $B_1, B_2, \ldots$ とし, $B_n$ の指示函数を $e_n$ とする. 今, 以下のように $S$ の上の実数函数 $f:S \longrightarrow \mathbb{R}$ を定義する.

\begin{align} f(x) = \sum_{n=1}^\infty \frac{2 e_n(x)}{3^n}. \end{align}

すると, $f(S)$ はCantor集合 $\bm{K}$ の部分集合となる. なぜなら,

\begin{align} p \in f(S) = \sum_{n=1}^\infty \frac{2 e_n(S)}{3^n} \notag \end{align}

のとき, $e_n(S)$ が $0$ か $1$ しか取らないことより, $2 e_n(S)$ は $0$ か $2$ しか取らない. 3進表記したときに, $0$ か $2$ しか現れないのが Cantor集合の性質であったので, $p \in \bm{K}$ であるとわかる. よって, $f(S) \subset \bm{K}$. また, これより $f$ は $P$ 可測 ( 可測$\cD(P)/\cB(\mathbb{R})$ ) であるとわかる.

$Q = Pf^{-1}$ とすると, $\mathbb{R}$ は可分距離空間なので, $Q$ は $\mathbb{R}$ 上の正則確率測度 ( 補題2.3 ) . これで, あとは $(S, P) \sim (\mathbb{R}, Q)$ を示せば証明終である.

$x, y \in S$, $x \neq y$ とすると, $n$ をうまく選んで $x \in B_n$, $y \notin B_n$ とできるので $e_n(x) \neq e_n(y)$, 即ち $f(x) \neq f(y)$ とできる. よって, $f$ は単射である. さらに, $f$ の値域を $T = f(S) \subset \mathbb{R}$ と制限することで全単射 $f' : S \longrightarrow T$ が得られる. $f^{-1}(T) = S$ であるから, $Q(T) = Pf^{-1}(T) = 1$. よって, $Q_T := Q|_T : T \longrightarrow \mathbb{R}$ は $T$ 上の確率測度である.

$f(A) = f'(A) \subset T$ なので ( $S \subset A$ なので )

\begin{align} A \in \cD(P) \Longleftrightarrow f'(A) \in \cD(Q_T), \end{align}

さらに,

\begin{align} A \in \cD(P) \Longrightarrow Q_T(f'(A)) = Pf^{-1}(f(A)) = P(A). \end{align}

よって,

\begin{align} A \in \cD(P) \Longleftrightarrow f'(A) \in \cD(Q_T) \Longrightarrow Q_T(f'(A)) = P(A) \end{align}

が成立し, $(S, P) \approx (T, Q_T)\;(f')$. よって, $(S, P) \sim (\mathbb{R}, Q)$ がいえた.

$\blacksquare$

感想・参考文献

感想

本記事を書くに当たって特に勉強になったのは「可分」という性質の使い方である. 集合論的な定義は知っていたが, 今ひとつ使いどこがわかっていなかった. 可分集合は, 稠密な可算集合が取れるので, 有限個の閉球でいくらでも精密に集合を近似できるというのは, 便利だなと思う.

定理2.6のステートメント自体は, そうなんだ...って感じやけど ( まだ凄さがわからない ) , その証明には多くの今まで学んできた知識が必要で勉強になった. すでに正則, 標準など多くの性質がでてきているが, 伊藤『確率論』は3章になると分離, 完全などさらなる用語がでてきて頭がちんぷんかんぷんになる. 少なくとも2章ででてくる用語については, 手にとるように分かるようになっていないと3章は太刀打ちできないと思って一連の解説記事を書き始めたが, 一段落した気持ちである.

次 ( セクション2.5 ) からは雰囲気がかわり, 一次元の分布になるとともに, いよいよ正規 ( Gauss ) 分布などがでてくる. さしあたり次の個人的なゴールは, 「中心極限定理」の厳密な証明である.

参考文献

伊藤清確率論 (岩波基礎数学選書)

この記事のTOP BACK TOP