ジョルダン標準形

この補題の内容自体は, 線型代数の内容というよりより環論の範疇だと思う. イデアルや体といったキーワードで調べるとより一般化された証明がある.

$M_i(x)\;(i = 1, \ldots, s)$ を任意の多項式とし,

なる形で表される多項式 $g(x)$ の全体を $\mathfrak{A}$ とする. これは, 以下の性質をもつ.

1. $g_1(x), g_2(x) \in \mathfrak{A} \Longrightarrow g_1(x) + g_2(x) \in \mathfrak{A},$
2. $g(x) \in \mathfrak{A},\;{}^{\forall}M(x) \Longrightarrow M(x)g(x) \in \mathfrak{A}.$

今, $\mathfrak{A}$ に属する多項式 ( $\neq 0$ ) のうち, 次数が最低のものを $g_0(x)$ とする. これで, 任意の $g(x) \in \mathfrak{A}$ をわると,

とかけて, $g(x), g_0(x) \in \mathfrak{A}$ なので, i), ii) より $h(x) \in \mathfrak{A}$. しかも, 上の多項式の割り算よりあきらかに, $h(x)$ の次数 $\lt g(x)$ の次数である. ところが, $g_0(x)$ の決め方を思い出すと, $h(x) = 0$ でしかありえない. つまり, $g(x) = M(x)g_0(x)$, 則ち $\mathfrak{A}$ は $g_0(x)$ の倍数全体の集合と一致する.

今, $f_i(x) \in \mathfrak{A}\;(i = 1, \ldots, s)$ であるから, $g_0(x)$ は $f_1(x), \ldots, f_s(x)$ の公約数である. 一方, $g_0(x) \in \mathfrak{A}$ であるから,

と表される ( 証明の一文目をみよ ) . よって, $g_1(x)$ を $f_1(x), \ldots, f_s(x)$ の任意の公約数とすれば, 上式の両辺が $g_1(x)$ で割れるということなので, $g_1(x)$ は $g_0(x)$ の約数である. すなわち, $g_0(x)$ は $f_1(x), \ldots, f_s(x)$ の最大公約数である.

さて, 仮定より $f_1(x), \ldots, f_s(x)$ の最大公約数は $1$ であるので, $g_0(x) = 1$ としてよく, \eqref{ideal} における $M_i(x)$ が求める多項式である.

$\blacksquare$

　$V^n$ が直和分解できること 　
$A$ の固有多項式 $f_A(x)$ は, $|A - xE|$ である. これを, 相異なる一次因数の冪の積に分解する.

とする. さらに, 以下のように $f_i(x)$ を定義する. これらは共通因子を持たない.

よって, 補題１により, ある $M_1(x), \ldots, M_s(x)$ があって,

となる. ここで, $x = A$ を代入して,

補題１の証明で $x$ を $A$ で置き換えて考えて, 共通因子をもたない行列多項式の最大公約数は $E$ ( 単位行列 ) だから上式がなりたつ, という考え方でよいのだろうか？ ここでさらに, $A_i = M_i(A)f_i(A)$ とおくと,

ここで,

である. なぜなら, \eqref{xxx} より, $A_iA_j \;(i \neq j)$ は必ず $f_A(A)$ を因数にもつが, Hamilton-Cayleyの定理 ( $f_A(A) = 0$ ) より, 上式がなりたつ. \eqref{yyy}, \eqref{zzz} より,

がなりたち, これは, $A_i$ が冪等行列であることを示している. 冪等行列があれば, $V^n$ は, 部分空間

の直和に分解される. 冪等行列の基本的な性質で, 証明略.

　$A_i V^n$ が $\widetilde{W}_{{\alpha}_{i}}$ と一致すること　
① $A_i V^n \subset \widetilde{W}_{{\alpha}_{i}}$ を示す.
$f_i(x)$ の定義\eqref{xxx}より,

よって, $x = A$ を代入し, Hamilton-Cayleyの定理 ( $f_A(A) = 0$ ) より,

両辺に $M_i(A)$ をかけて, $A_i = M_i(A)f_i(A)$ を思い出すと,

よって, $A_i V^n \subset \widetilde{W}_{{\alpha}_{i}}$.

② $A_i V^n \supset \widetilde{W}_{{\alpha}_{i}}$, つまり $\bm{x} \in \widetilde{W}_{{\alpha}_{i}} \Rightarrow \bm{x} \in A_i V^n$ を示す.
$\bm{x} \in \widetilde{W}_{{\alpha}_{i}}$ とすると, ある $l$ に対して $(A - \alpha_i E)^{l}\bm{x} = 0$. \eqref{www} より, $(x - \alpha_i)^{l}$ と $M_i(x)f_i(x)$ とは共通因子をもたない. ( 理由. もし共通因子をもつなら, 共通因子は $x - \alpha_i$ であるが, $f_i(x)$ の定義より $M_i(x)f_i(x)$ のなかで $x - \alpha_i$ を因子として持ちうるのは $M_i(x)$ である. しかし, もしそうだとすると, そもそも $f_j(x)\;(i \neq j)$ が $x - \alpha_i$ を因子として持つため, \eqref{www} の左辺は $x - \alpha_i$ で割り切れることになってしまう. )

よって, 補題１よりある多項式 $M(x)$, $N(x)$ があって,

即ち,

ゆえに, $\bm{x} \in A_i V^n$.

$\blacksquare$

$\dim{\widetilde{W}_{{\alpha}_{i}}} = n_i^{\prime}$ とする. そもそも, $\widetilde{W}_{{\alpha}_{i}}$ は$A$−不変であったので, 直和分解\eqref{dpdecomp}に即して底をとり, \eqref{dpdecomppre} と同じようにすることで,

となる. ここで, $A^{(i)}$ は $A$ が $\widetilde{W}_{{\alpha}_{i}}$ に引き起こす一次変換を表す $n_i^{\prime}$ 次の行列である. いま, $n_i^{\prime}$ 次単位行列を $E_{n_i^{\prime}}$ とすれば, \eqref{wideEigSpDef} により, $N_i = A^{(i)} - E_{n_i^{\prime}}$ は冪零. また, 冪零行列の固有値は, 明らかに $0$ だけであるので, $n$ 次冪零行列 $A$ の固有多項式 $f_A(x) = x^n$ となることを踏まえ,

より,

よって, \eqref{aaa} より,

よって, $n_i^{\prime} = n_i$ でなければならない.

$\blacksquare$

$N$：冪零行列, $N^{\nu - 1} \neq 0$, $N^{\nu} = 0$, つまり, $N$ を $\nu$ 回掛けるとゼロになる冪零行列とする.

とすると, もちろん全ての $\bm{x}\in V^n$ に対して $N^{\nu}\bm{x} = \bm{0}$ なので $V^n = W^{(\nu)}$で,

今, $\dim{W^{(i)}} = m_i$, $m_i - m_{i-1} = r_i\; (i = 1, \ldots ,n)$, $m_0 = 0$, とおく. つまり, 上の式になぞらえてかくと,

ここで, $W^{(i-1)}$ の任意の基底に $m_i - m_{i-1} = r_i$ 個のベクトル $\vecseq{\bm{a}}{1}{r_{\nu}}$ を付け加えて $W^{(i)}$ の基底になるようにできる. つまり,

このとき,

ゆえに $\vecseq{N\bm{a}}{1}{r_{\nu}} \in W^{(\nu-1)}$ である. ここで, 以下がなりたつ.

• $\vecseq{N\bm{a}}{1}{r_{\nu}}$は一次独立.
• $ \{\{ \vecseq{N\bm{a}}{1}{r_{\nu}} \}\} \cap W^{(\nu-2)} = \bm{0}$

なぜなら, $c_1N\bm{a}_1 + \cdots + c_{r_{\nu}}N\bm{a}_{r_{\nu}} ( \in W^{(\nu-2)} ) = \bm{0}$ とすれば,

\begin{align} 　 N^{\nu-2}(c_1N\bm{a}_1 + \cdots + c_{r_{\nu}}N\bm{a}_{r_{\nu}}) = N^{\nu-1}(c_1\bm{a}_1 + \cdots + c_{r_{\nu}}\bm{a}_{r_{\nu}}) = \bm{0}. \notag 　　\end{align}

すなわち, $c_1\bm{a}_1 + \cdots + c_{r_{\nu}}\bm{a}_{r_{\nu}} \in W^{(\nu-1)}$. ところが, \eqref{nustar}より, $c_1\bm{a}_1 + \cdots + c_{r_{\nu}}\bm{a}_{r_{\nu}}$ は, $\bm{0}$ 以外の $W^{(\nu-1)}$ の元たりえない. 今, $\vecseq{\bm{a}}{1}{r_{\nu}}$は一次独立であることを思い出すと, $c_1 = c_2 = \cdots = c_{r_{\nu}} = 0$ とわかる.

ここまでのことにより, $r_{\nu} \leq r_{\nu-1}$ である.
少しまとめるために, 今 $W^{(\nu)} \supset W^{(\nu-1)} \supset W^{(\nu-2)}$ だけに注目する. それぞれの次元の関係は, $m_{\nu} \geq m_{\nu-1} \geq m_{\nu-2}$ でその差分は, $r_{\nu}$, $r_{\nu-1}$ であった. \eqref{nustar}より, $\vecseq{\bm{a}}{1}{r_{\nu}}$ は $W^{(\nu)}$ の基底であるが $W^{(\nu-1)}$ の基底ではない $r_{\nu}$ 個のベクトルであった. では, $\vecseq{N\bm{a}}{1}{r_{\nu}}$ の $r_{\nu}$ 個のベクトルはどこに属するだろうか？ これは, $W^{(\nu-1)}$ に属するので, 再び\eqref{nustar}より $\{\{ \vecseq{\bm{a}}{1}{r_{\nu}} \}\}$ には属さないし, $ \{\{ \vecseq{N\bm{a}}{1}{r_{\nu}} \}\} \cap W^{(\nu-2)} = \bm{0}$ より $W^{(\nu-2)}$ にも属さない. 即ち, $\vecseq{\bm{a}}{r_{\nu}+1}{r_{\nu-1}}$ の $r_{\nu-1}$ 個の基底で張られる空間に属する. これから, $r_{\nu} \leq r_{\nu-1}$ がわかる.
したがって, $r_{\nu-1} - r_{\nu}$ 個のベクトル $\vecseq{\bm{a}}{r_{\nu}+1}{r_{\nu-1}}$ を適当に取れば, $W^{(\nu-2)}$ の基底に $\vecseq{N\bm{a}}{1}{r_{\nu}}, \vecseq{\bm{a}}{r_{\nu}+1}{r_{\nu-1}}$ を付け加えて $W^{(\nu-1)}$ の基底になるようにできる. このとき,

\eqref{nain}とその下の命題と同じようにして,

は一次独立かつ,

である. よって, $r_{\nu-1} \leq r_{\nu-2}$. これを繰り返して,

でありさらに,

となる. ここまででわかったことをまとめると, 以下のような図にできる.

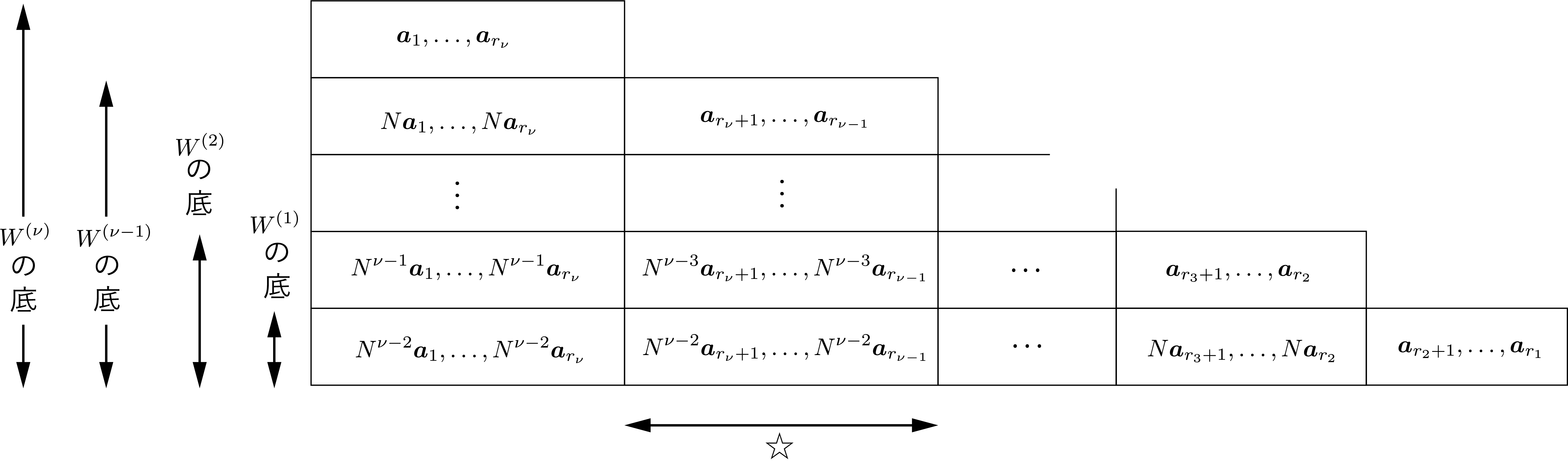
この図に入っているベクトル全体が $V^n$ の基底であるので, $V^n$ の基底全体は次のように表される.

さて, $r_{i+1} +1 \leq j \leq r_i$ に対して,

は明らかに$N$-不変な部分空間である.
ここで, 今度は上の図を縦に切ってみていることになる. 例えば, $i = r_{\nu-1}$ のときは, 上図の☆印のエリアを対象としている. このエリアには, $r_{\nu-1} - r_{\nu} (\geq 0)$ 個のベクトルが入った部屋が縦に $\nu-1$ 段並んでいるように描かれているが, 見方をかえれば, $\nu-1$ 個のベクトルが横に $j = 1, \ldots, r_{\nu-1} - r_{\nu}$ 本並んでいるようにみえる. その一本一本が張る空間を \eqref{tatetate} は示している. 例えば, $j=1$ のときに張られる空間は $\{\{ \bm{a}_{r_{\nu}+1}, N\bm{a}_{r_{\nu}+1}, \ldots, N^{\nu-2}\bm{a}_{r_{\nu}+1} \}\}$ であるので, この空間の元はこれらの一次結合で表される. それに $N$ を掛ければ, 再び元の空間に属する ( $N$-不変 ) ことは明らかだろう.
この底 ( $\{\{ \bm{a}_j, N\bm{a}_j, \ldots, N^{i-1}\bm{a}_j \}\}$ ) に関して $N$ を表せば,

となる. これは,

であることを示す. ところで, $V^n$ は ( 上の図よりもわかるように ) \eqref{tatetate}のいくつかの直和に分解されるのだった. よって $N$ は

なる形の行列をいくつか対角に並べてできる行列に相似である.

$\blacksquare$