MATLABで『時系列解析入門』８章

最終更新：2021/08/05

局所定常ARモデル.

非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

任意個の区間への自動分割

アルゴリズム

教科書に詳しいアルゴリズムはあるので, そちらを見てもらいたい. コードと地震波データ(MYE1F)に適用した結果を示す.

簡単に地震波データで説明する.

地震波データ ( 長さ2600 ) を各々長さ150の少区間 $A_1, A_2, \ldots$ に分ける.
区間 $A_1$ と $A_2$ にARモデルを適用 ( 最大次数は10とした ) し, 各々の区間の最小AICの和を分割モデルのAIC：$\mathrm{AIC}_D$ とする.
併合区間 $[ A_1, A_2 ]$ にARモデルを適用し, 最小AIC ( $\mathrm{AIC}_P$ ) を計算する.
$\mathrm{AIC}_P$ と $\mathrm{AIC}_D$ を比較し, $\mathrm{AIC}_P$のほうが小さければ区間を併合し, $\mathrm{AIC}_D$ が小さければ区間は分割したままにする.
これを繰り返す.

というアルゴリズムである.

コード

正直効率的でない部分もあるが, そんなに重い計算でもないので.

MATLAB

function [ns, span, ms, aicDP, spec, f] = lsar(d, maxArOrder, ns0, method)
% LSAR
% 
% INPUTS
% maxArOrder : ARモデルの最大次数 
% ns0        : 基本小区間の長さ
% method: 1: levinson
%         2: Leastsquare
%         3: Normal Equation
% 
% OUTPUTS
% ns   : 各局所定常スパンのデータ数
% span : 局所定常スパンの始点と終点
% ms   : 分割モデルの次数
% aicDP: 分割モデルのAICと併合モデルのAIC
% spec : 各局所定常スパンのパワースペクトル
% f    : パワースペクトルの周波数

% preprocessings
d     = d - mean(d);
L     = length(d);
span  = zeros(ceil(L/ns0), 2);
ns    = zeros(ceil(L/ns0), 1);
aicDP = zeros(floor(ceil(L/ns0))-2, 2);

% step 1
[aic, ~, ~, maic] = myAr(d(1:ns0), maxArOrder, method);
aic0       = aic(maic+1);
k          = 1;
span(1, 1) = maxArOrder + 1;
span(1, 2) = maxArOrder + ns0;
ns(1)      = ns0 - maxArOrder;

% step 2- 
count = 1;
while L - span(k, 2) + 1 > ns0
    
    % divided model
    [aic, ~, ~, maic] = myAr(d(span(k, 2):span(k, 2)+ns0), maxArOrder, method);
    aic1 = aic(maic+1);
    aicD = aic0 + aic1;
    
    % pooled model
    [aic, ~, ~, maic] = myAr(d(span(k, 1):span(k, 2)+ns0), maxArOrder, method);
    aicP = aic(maic+1);
    
    aicDP(count, :) = [aicD aicP];
    if aicD < aicP
        k          = k+1;        
        span(k, 1) = span(k-1, 2) + 1;
        span(k, 2) = span(k-1, 2) + ns0;
        ns(k)      = ns0;
        aic0       = aicD;
    else
        span(k, 2) = span(k, 2) + ns0;
        ns(k)      = ns(k) + ns0;
        aic0       = aicP;
    end
    count = count + 1;
end

span = span(span(:, 1)~=0, :);
ns   = ns(ns ~= 0);

% plot
t = tiledlayout(3, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile(1, [2, 1]);
    for I = 1:size(span, 1)
       plot(span(I, 1):span(I, 2), d(span(I, 1):span(I, 2))); hold on
    end
    temp = maxArOrder:ns0:length(d);
    xline(temp(2:end-1));
    ylabel('Data'); xticks({}); xlim([1 L]);
nexttile
    bar(temp(2:end-1), aicDP(:, 1)-aicDP(:, 2), 0.5, 'LineStyle', 'none')
    xlim([1 L]); ylabel('AIC_{D} - AIC_{P}')

% calculate local stationary spectrum
nd = length(ns);
ms = zeros(1, nd);
spec = zeros(nd, length(0:0.001:0.5));
for I = 1:nd
    [~, Arcoef, s2, maic] = arNormaleq(d(span(I, 1):span(I, 2)), maxArOrder);
    a = Arcoef.(['order', num2str(maic)]);
    [s, f] = spectrumARMA(a, 0, s2(maic+1));
    spec(I, :) = s;
    ms(I) = maic;
end
end

なお, 函数myARは, 今までに作ったYule-Walker法, Householder法, 正規方程式を用いたARモデル推定の函数をまとめたものである. Householder法, 正規方程式は最小二乗法なので結果はおなじになる. 検算用である.

MATLABコード

MATLAB

function [aic, Arcoef, s2, maic] = myAr(d, M, method)
%MYAR
%
% INPUT
% d:data
% M:maximum AR degree (lag)
% method: 1: levinson
%         2: Leastsquare
%         3: Normal Equation
% 
% OUTPUT
% aic     : AIC
% Arcoef  : AR coefficient (structure)
% s2      : sigma^2
% maic    : The order which provides the minimum AIC

switch method
    case 1
        [aic, Arcoef, s2, maic] = arLevinson(d, M);

    case 2
        [aic, Arcoef, s2, maic] = arLeastsquares(d, M);

    case 3
        [aic, Arcoef, s2, maic] = arNormaleq(d, M);

    otherwise
        warning('Unexpected method type.')
end
end

地震波へ適用

Yule-Walker法で行った結果はよく分割してくれている. $\mathrm{AIC}_D - \mathrm{AIC}_P$ は, 正の値だと併合モデルが選択されたことを示す.

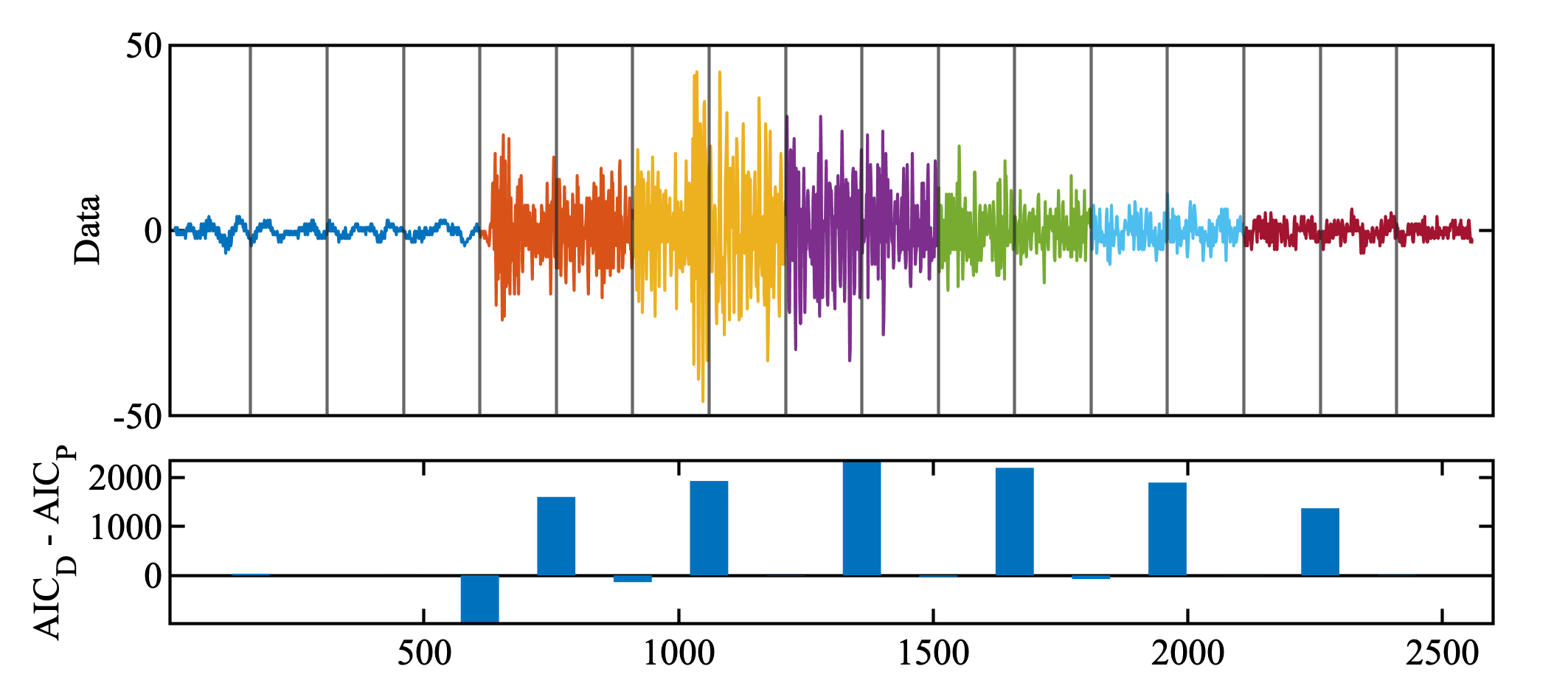
MATLABコード

MATLAB

d = mye1f;
maxArOrder = 10; 
ns0        = 150;
[ns, span, ms, aicDP, spec, f] = lsar(d, maxArOrder, ns0, 1);

各局所定常スペクトルもみておく. 横軸 $f$, 縦軸 $\log_{10}{p(f)}$ である.

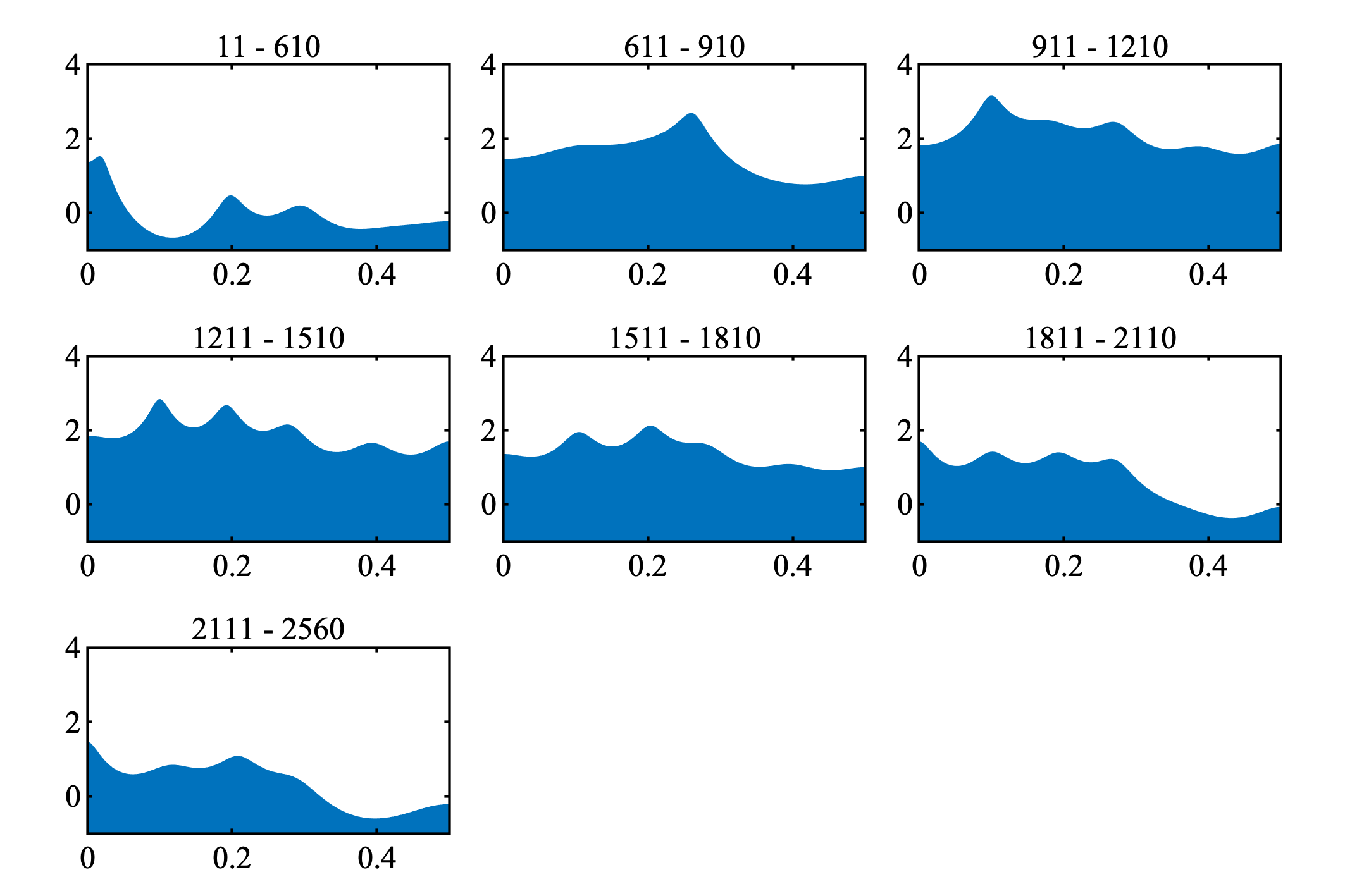
MATLABコード

MATLAB

figure;
nTile = size(spec, 1);
t = tiledlayout(ceil(sqrt(nTile)), ceil(sqrt(nTile))); t.Padding = 'compact'; t.TileSpacing = 'compact';
for I = 1:nTile
    nexttile    
    area(f, log10(spec(I, :)), 'BaseValue', -1, 'LineStyle', 'none');
    ylim([-1 4])
    xlim([0 0.5])
    title([num2str(span(I, 1)) ' - ' num2str(span(I, 2))])
end

白色雑音へ適用

このモデルを白色雑音に適用したらどうなるのだろう？ AICも確率的に動くので, 分割モデルは次数が大きい ( 罰金が大きい ) とはいえ一定の確率で分割モデルが選ばれてしまうはずである.

ほら！

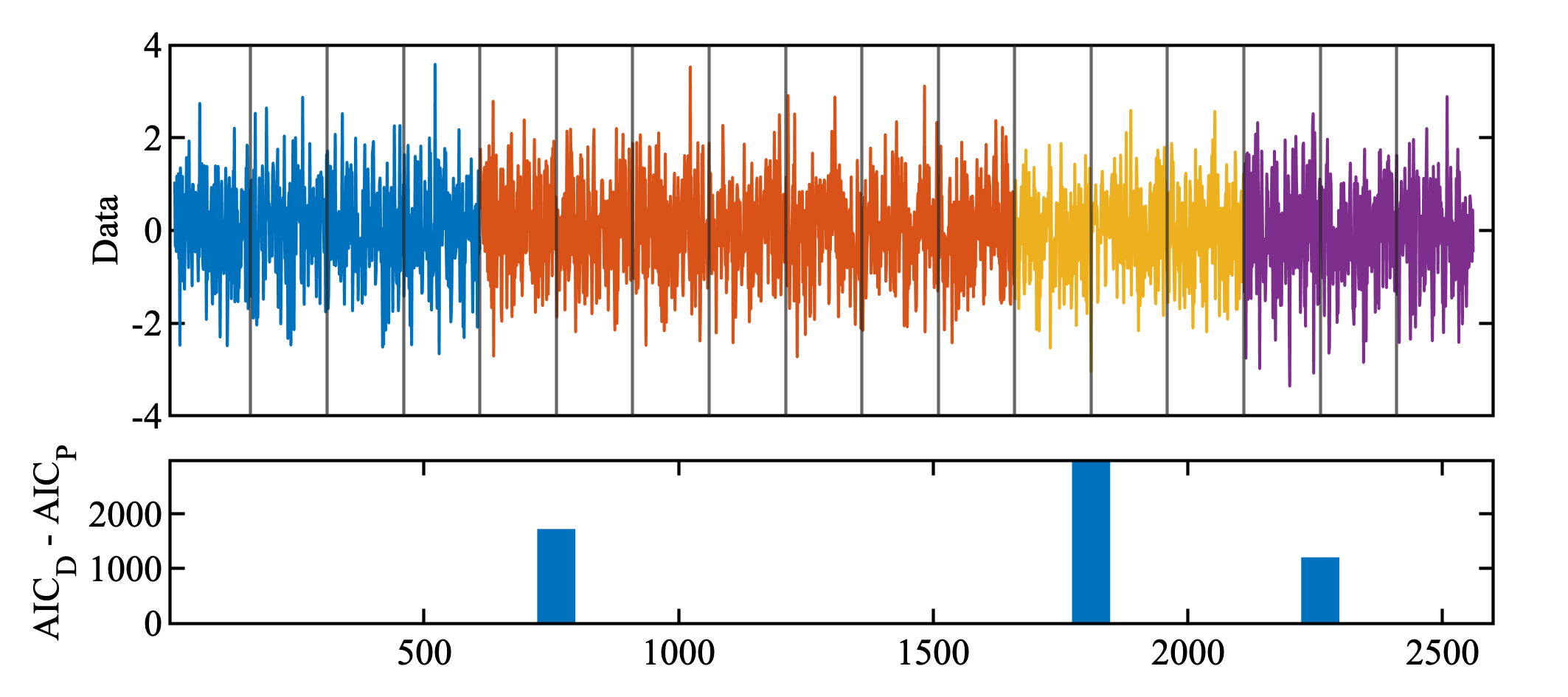
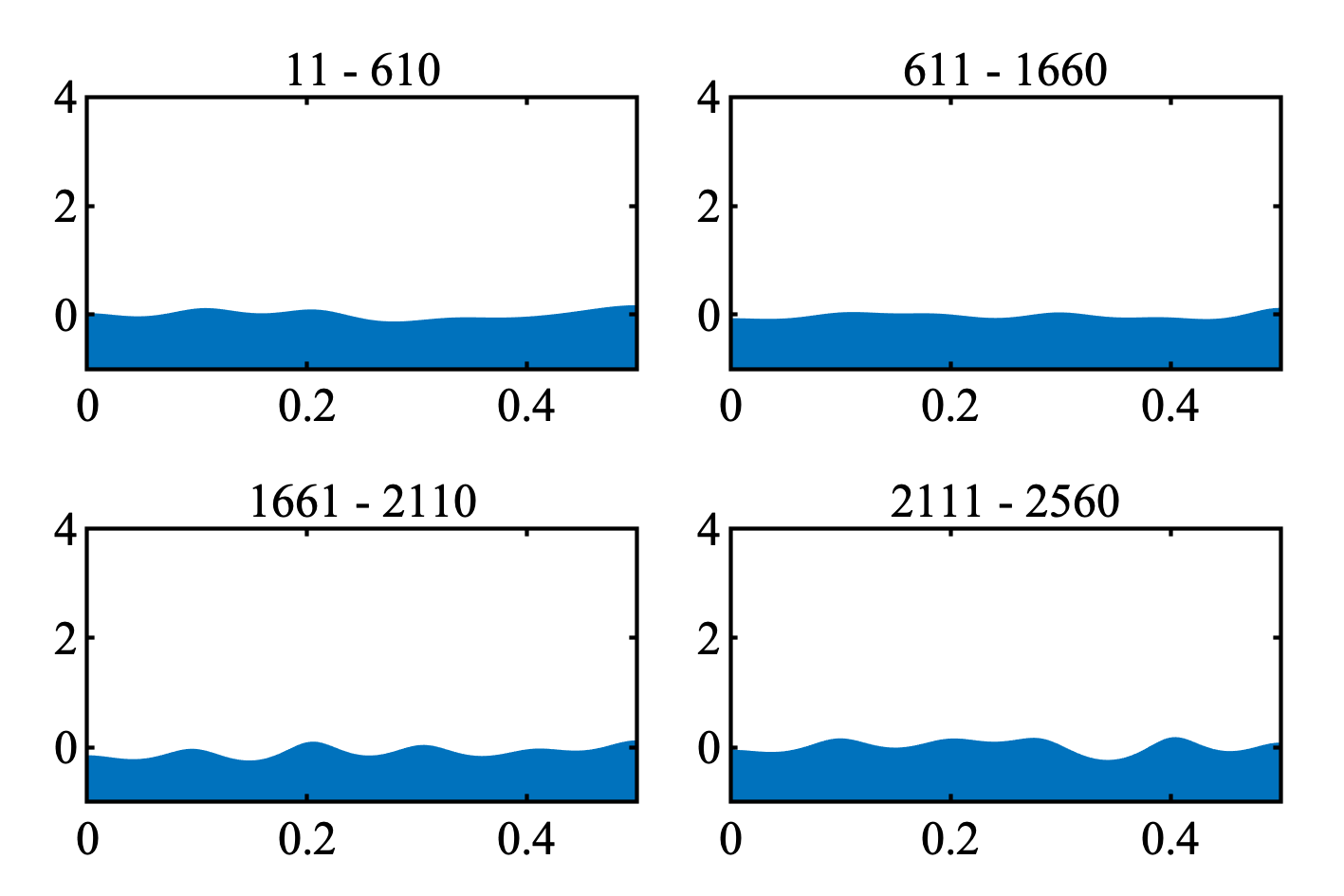
ただ, 局所定常スペクトラムをみれば, 意味のある分割かはそこそこわかると思う.

変化時点の精密な推定

アルゴリズム

理屈はシンプル. 信号を分ける点を一つずつずらしていき, 前半のAICと後半のAICの和をもとめ, それが最小になる点を変化時点とする.

ただ, 膨大な量の計算量になるので, 教科書通りハウスホルダー法で行っている. 教科書には前半にハウスホルダー法を適用するための行列 ( 式8.22 ) が載っているが, 後半に対しては載っていないのでココに記しておく. もちろん, 載せるまでもなく自明なのだが, 結構添字が複雑になるので.

まず $\vecseq{y}{n_1+1}{N}$ にARモデルを当てはめる. 前半を計算するための行列 ( 式8.22 ) に対応する後半の行列は,

\begin{align}\large{ X_0 = \begin{pmatrix} y_{n_1 + m} & y_{n_1 + m-1} & \cdots & y_{n_1 +1} & y_{n_1 + m + 1} \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ y_{N-1} & y_{N-2} & \cdots & y_{N-m} & y_{N} \\ \end{pmatrix} }\end{align}

である. $p$ 番目に上三角行列の下に追加すべき行ベクトル ( 式8.17の下段 ) は,

\begin{align}\large{ ( y_{n_1 + m - p}, y_{n_1 + m - p - 1}, \ldots, y_{n_1 - p + 1}, y_{n_1 + m - p + 1} ) }\end{align}

となる.

コード

kやcなど変な変数があるのは, 最初 $p$ を増やす間隔も設定しようと思ったから. でもめんどくさくなってやめた.

MATLAB

function [aic, aicmin, changePoint] = lsarChgpt(d, maxArOrder, subinterval, candidate)
% LSARCHGPT
% INPUTS
% d           : 1 dim. data
% maxArOrder  : ARモデルの最大次数
% subinterval : モデリングに使用するデータ区間の始点と終点 [n0, ne]
% candidate   : 変化点の候補点の最小値と最大値 [n1, n2] 十分に[n0, ne]に含まれること. 
% 
% OUTPUTS
% aic         : 区間[n1, n2]で当てはめられたARモデルのAIC
% aicmin      : 最小AIC
% changePoint : 推定された変化点

M = maxArOrder;
d = reshape(d, [], 1);
% d = d - mean(d);
d = d(subinterval(1):subinterval(2));
n0 = candidate(1) - subinterval(1) + 1;
n1 = candidate(2) - subinterval(1);
L  = candidate(2) - candidate(1) + 1;
k  = 1;
l  = floor(L/k);

p  = 1;
% Former part
XF = zeros(n0-M, M+1);
aicF = zeros(1, l);
for col = 1:M
    begin = M - col + 1;
    XF(:, col) = d(begin:n0-col);
end
XF(:, end) = d(M+1:n0);

[~, SF]     = qr(XF); % householder
SF          = SF(1:M+1, 1:M+1);
s2F         = flipud(cumsum(flipud(SF(:, end).^2))) / (n0-M);
aicFTmp     = (n0 - M) * log(s2F) + 2*((0:M)'+1);
aicF(p)     = min(aicFTmp);

% Latter part
N  = length(d);
XL = zeros(N-n1-M, M+1);
aicL = zeros(1, l);
for col = 1:M
    begin = n1 - col + M + 1;
    XL(:, col) = d(begin:N-col);
end
XL(:, end) = d(n1+M+1:N);
[~, SL]     = qr(XL); % householder
SL          = SL(1:M+1, 1:M+1);
s2L         = flipud(cumsum(flipud(SL(:, end).^2))) / (N-n1-M);
aicLTmp     = (N-n1-M) * log(s2L) + 2*((0:M)'+1);
aicL(p)     = min(aicLTmp);

for I = 1:l-1
    c = p*k;
    % Former part
    [~, SF]     = qr([SF; [d(n0+c-1:-1:n0-M+c)' d(n0+c)]]);
    SF          = SF(1:M+1, 1:M+1);
    s2F         = flipud(cumsum(flipud(SF(:, end).^2)))  / (n0-M+c);
    aicFTmp     = (n0-M+c) * log(s2F) + 2*((0:M)'+1);

    % Latter part
    [~, SL]     = qr([[d(n1+M-c:-1:n1-c+1)' d(n1+M-c+1)]; SL]);
    SL          = SL(1:M+1, 1:M+1);
    s2L         = flipud(cumsum(flipud(SL(:, end).^2)))  / (N-n1-M+c);
    aicLTmp     = (N-n1-M+c) * log(s2L) + 2*((0:M)'+1);

    p           = p + 1;
    aicF(p)     = min(aicFTmp);
    aicL(p)     = min(aicLTmp);
end

aic = fliplr(aicL) + aicF;
[aicmin, changePoint] = min(aic);
changePoint = candidate(1) + changePoint*k;
end

地震波への適用

再び地震波のデータへ適用する. これは完璧でしょう. 久々に教科書とほぼ完全に一致した. これは, 比較的変化が明確な常微動→P波への変化

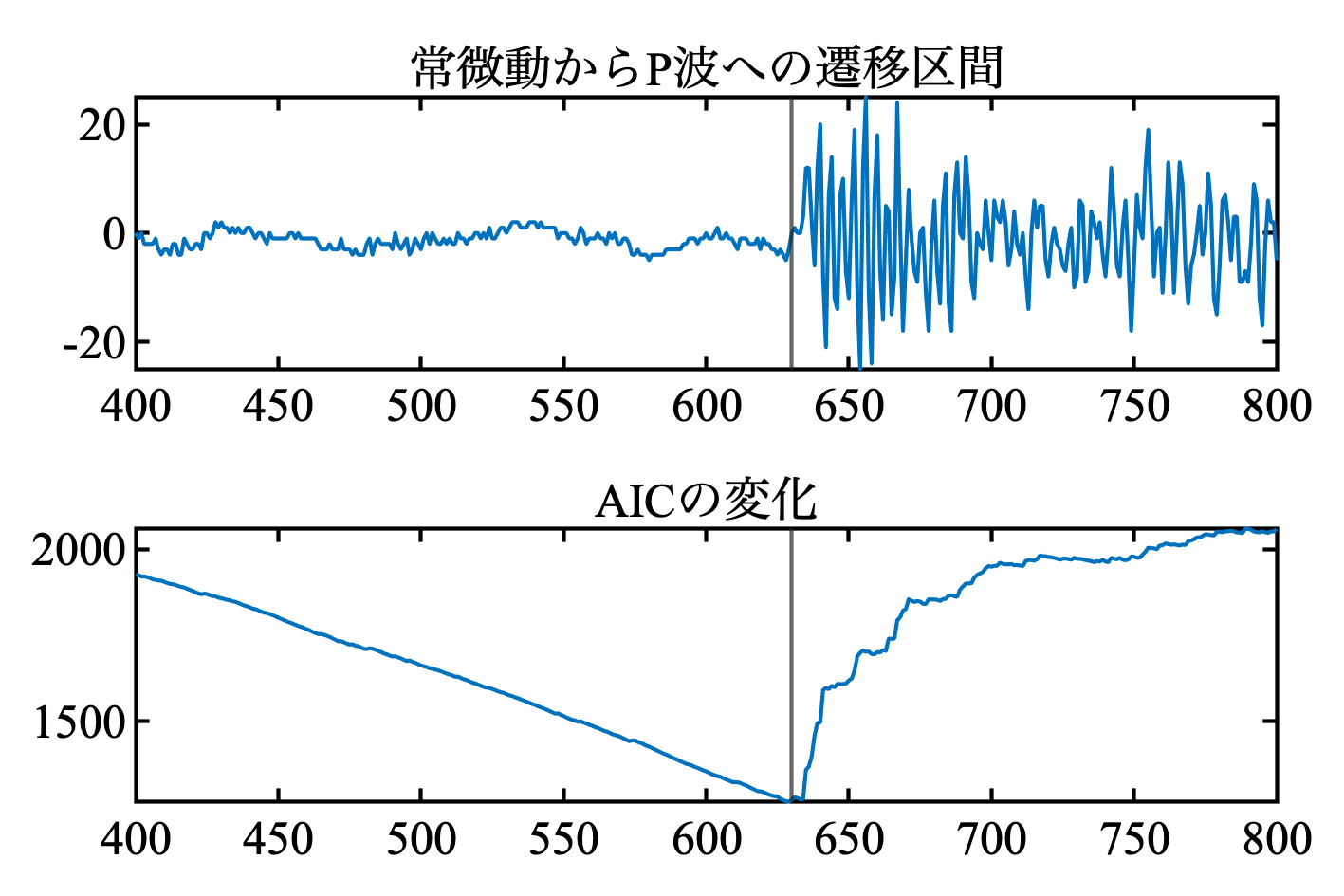
MATLABコード

MATLAB

t = tiledlayout(2, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
    plot(candidate(1):candidate(2), d(candidate(1):candidate(2)))
    title('常微動からP波への遷移区間')
    xlim([candidate(1), candidate(2)])
    xline(changePoint)
nexttile
    plot(candidate(1):candidate(2), aic)
    xline(changePoint)
    title('AICの変化')

これは, P波→S波への変化. 教科書と若干形が違うが, 変化点はおなじになった. 一点ずつ変化点をずらしながら愚直に両側のAICを計算してみても同じ形になったので, とりあえずよしとする.

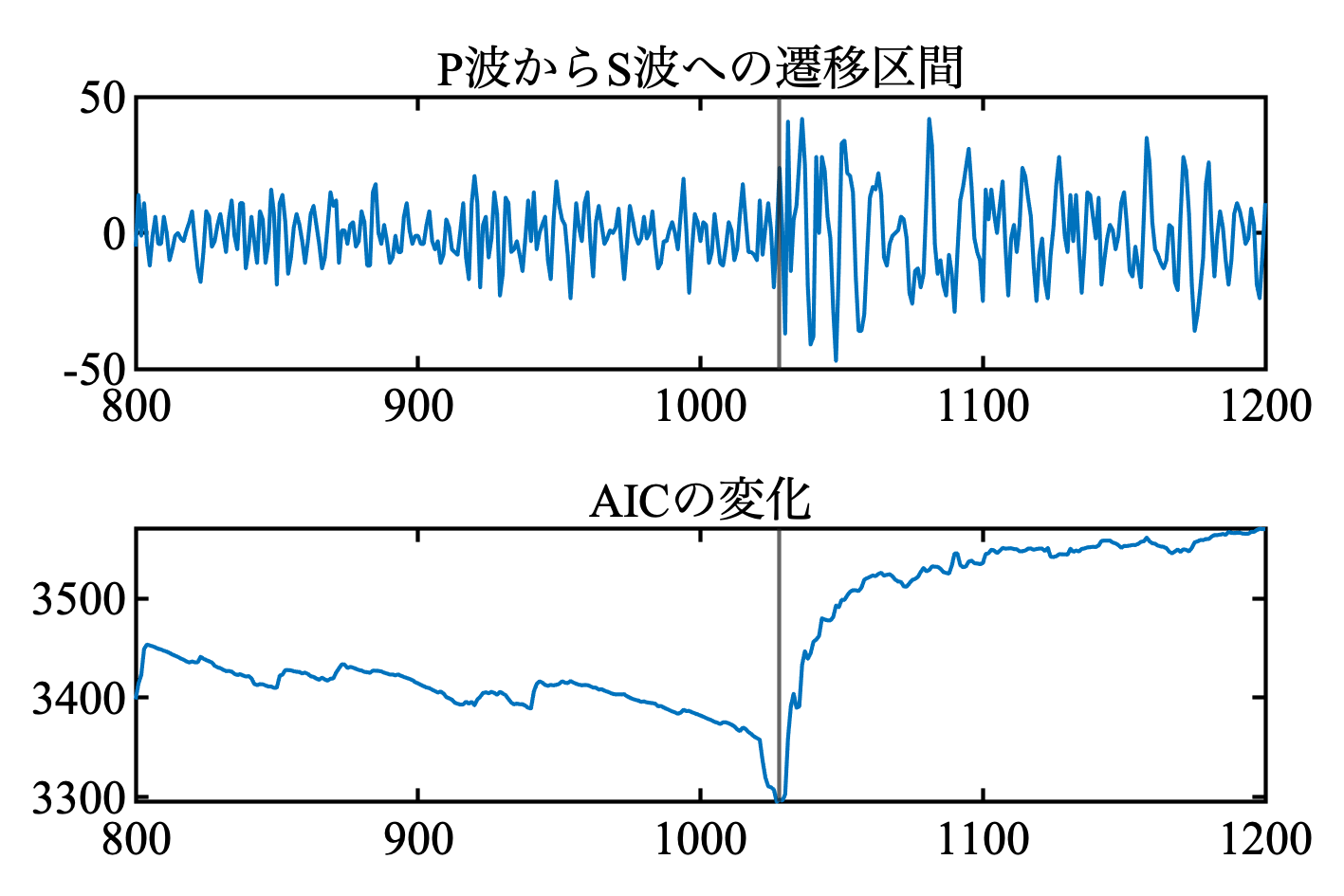
おまけ

変化点をずらしながら, 愚直に両側のAICを計算する函数を作った. 非効率なので計算速度は落ちるが, 以下を目的とした.

検算用
任意の固定変化点間隔
最小二乗法以外の適用

MATLAB

function [aic, aicmin, changePoint] = lsarChgpt2(d, maxArOrder, subinterval, candidate, interval, method)
% LSARCHGPT2
% INPUTS
% d           : 1 dim. data
% maxArOrder  : ARモデルの最大次数
% subinterval : モデリングに使用するデータ区間の始点と終点 [n0, ne]
% candidate   : 変化点の候補点の最小値と最大値 [n1, n2] 十分に[n0, ne]に含まれること. 
% interval    : 変化点候補の間隔
% method: 1: levinson
%         2: Leastsquare
%         3: Normal Equation
% 
% OUTPUTS
% aic         : 区間[n1, n2]で当てはめられたARモデルのAIC
% aicmin      : 最小AIC
% changePoint : 推定された変化点

M = maxArOrder;
chgPtCandidate = candidate(1):interval:candidate(2);
L = length(chgPtCandidate);
aic = zeros(1, L);
for I = 1:L
    
    d1 = d(subinterval(1):chgPtCandidate(I));
    d2 = d(chgPtCandidate(I)+1:subinterval(2));
   
    [aict, ~, ~, maic] = myAr(d1, M, method);
    aic1 = aict(maic+1);
    [aict, ~, ~, maic] = myAr(d2, M, method);
    aic2 = aict(maic+1);
    aic(I) = aic1+aic2;
end

[aicmin, changePoint] = min(aic);
changePoint = chgPtCandidate(changePoint);

end

変化時点の事後確率

地震波

「変化時点の精密な推定」のモデルで, AICが対数尤度と考えれば, 変化点を $j$ と考えたときの尤度は,

\begin{align}\large{ L(y \mid j) = \exp \left\{ -\frac{1}{2} \mathrm{AIC}_j \right\} }\end{align}

と考えられる. AICがバイアス補正された対数尤度という認識はあったが, AICから尤度を計算するという発想はなかった. 新鮮で面白い. よって, 事前分布として一様分布を想定すれば, 到着時刻の事後分布が,

\begin{align}\large{ p(j \mid y) \propto \exp \left\{ -\frac{1}{2} \mathrm{AIC}_j \right\} }\end{align}

をみたす. 確率密度にするならば, 正規化すればよい. 教科書の例を再現する.

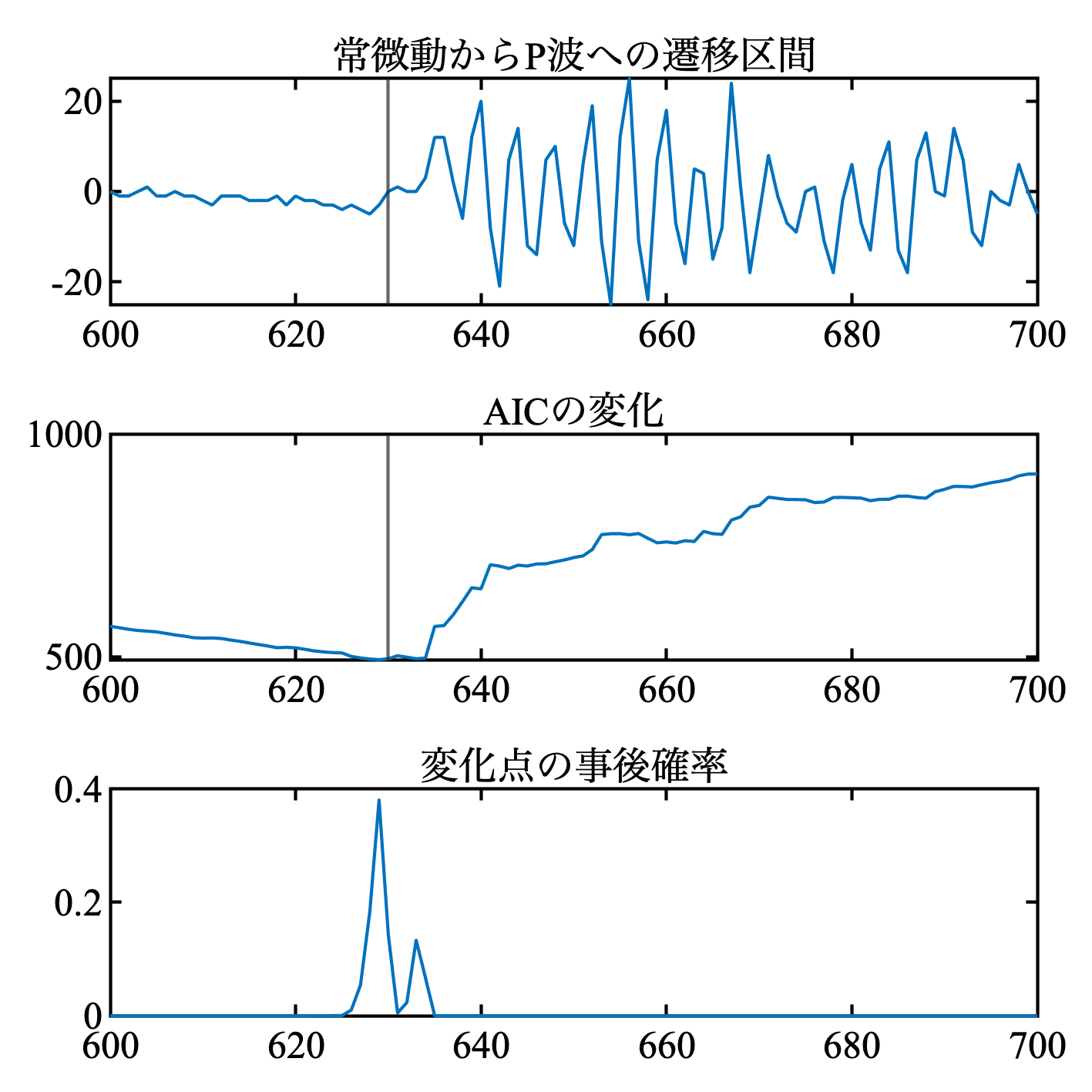
MATLABコード

MATLAB

d = mye1f;
maxArOrder = 10;
subinterval = [400, 800];
candidate = [600, 700];
[aic, aicmin, changePoint] = lsarChgpt(d, maxArOrder, subinterval, candidate);

t = tiledlayout(3, 1); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
    plot(candidate(1):candidate(2), d(candidate(1):candidate(2)))
    title('常微動からP波への遷移区間')
    xlim([candidate(1), candidate(2)])
    xline(changePoint)
nexttile
    plot(candidate(1):candidate(2), aic)
    xline(changePoint)
    title('AICの変化')
nexttile
    post = exp(-0.5 * (aic - min(aic)));
    post = post / sum(post);
    plot(post)
    title('変化点の事後確率')

主な参考文献

Rによる時系列モデリング入門

この記事のTOP BACK TOP