MATLABで『時系列解析入門』５章

最終更新：2021/06/08


非専門家が書いています. 十分に批判的に読んで頂くようお願いいたします. 間違い・疑問点などあれば, ぜひコンタクトフォームへ連絡いただけると幸いです.

Householder変換

Householder法を使って, 説明変数行列 $Z$ を上三角行列 $S$ に変換するということだが, 幸いMATLABには QR分解を行う函数があるので, そいつに頼る.

例えば, 以下の行列 $M$ を用意する. $$ M = \begin{pmatrix} 6.96 & 9.80 & 4.38 \\ 2.86 & 6.84 & 0.59 \\ 2.26 & 4.80 & 3.98 \\ 5.51 & 3.92 & 7.38 \\ 7.19 & 3.43 & 1.82 \\ 4.23 & 7.29 & 1.75 \end{pmatrix} $$

MATLABコード MATLAB 
rng(123)
M = rand(6, 3)*10;
これにQR分解を施すと,
MATLAB 
[Q,R] = qr(M);
次のように, 直交変換をあらわす行列 $Q$ と 上三角化された行列 $R$ が求まる. $$ M = QR, \\ {}\\ Q = \begin{pmatrix} -0.54 & -0.30 & 0.02 & -0.31 & -0.61 & -0.36 \\ -0.22 & -0.50 & 0.25 & 0.55 & 0.41 & -0.39 \\ -0.17 & -0.31 & -0.43 & -0.58 & 0.58 & 0.02 \\ -0.43 & 0.27 & -0.71 & 0.46 & -0.04 & 0.04 \\ -0.56 & 0.59 & 0.44 & -0.15 & 0.32 & -0.01 \\ -0.33 & -0.36 & 0.18 & 0.11 & -0.07 & 0.83 \end{pmatrix}, \\ {} \\ R = \begin{pmatrix} -12.72 & -13.82 & -8.05 \\ 0 & -7.43 & -0.37 \\ 0 & 0 & -5.58 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}. $$

最小二乗法

データとモデル

教科書に合わせて, 東京の最高気温データに, いろいろな次数の三角関数モデルをあてはめてみる.

name
\begin{align}\large{ y_n = a + \sum_{j=1}^m b_j \sin{j \omega n} + \sum_{j=1}^l c_j \cos{j \omega n} + \varepsilon_n. \notag }\end{align}
詳しくは教科書を見てほしいが, 例えば, 次数5のモデルは,
\begin{align} y_n = a + b_1 \sin{\omega n} + c_1 \cos{\omega n} + b_2 \sin{2 \omega n} + c_2 \cos{2 \omega n} + b_3 \sin{3 \omega n} + \varepsilon_n \notag \end{align}
である. 教科書に合わせて次数21までを検討する.

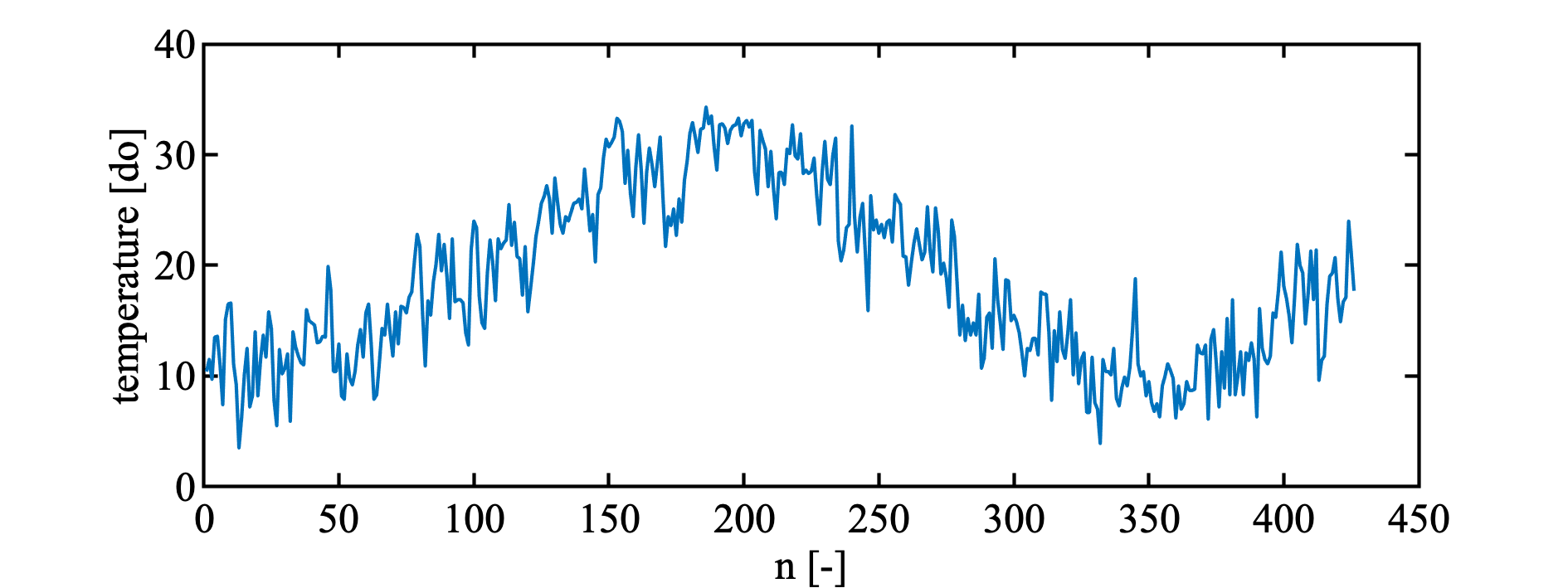
AICによる次数選択

以下のコード内で説明する. 残差分散を $\hat{\sigma}^2$ としたとき, AICは以下の式で求まる.

\begin{align}\large{ \mathrm{AIC} = N(\log(2 \pi \hat{\sigma}^2) + 1) + 2(j+1). \notag }\end{align}
ここで, $j$ はモデルの次数.

MATLAB 
d      = tokyo';       % データを縦ベクトルに
maxK   = 10;           % sin, cos 成分それぞれの ( 最大 ) 個数
om     = 2*pi/365;     % オメガの値, 教科書にならう

maxDeg = maxK*2+1;     % 最高次数
N      = length(d);    % データの長さ
n      = 1:N;          % 説明変数 ( グラフの横軸 ) 

% 式 ( 5.14 ) の右辺左側の行列Zを計算
Z = zeros(N, maxDeg);
Z(:, 1) = 1;
for k = 1:maxK
    Z(:, 2*k)   = sin(k*om*n);
    Z(:, 2*k+1) = cos(k*om*n);
end

% 式 ( 5.14 ) の右辺の行列Xを作る
X = [Z d];

% ハウスホルダー変換
[~,R] = qr(X);

% 式 ( 5.15 ) の行列
S = R(1:maxDeg+1, :);
s = S(:, end);       

% 式 ( 5.23 ) を用いて, 残差分散の推定値とAICを計算
sigma2_hat = zeros(1, maxDeg);
aic        = zeros(1, maxDeg);
for I = 1:maxDeg
    sigma2_hat(I) = sum(s(I+1:end).^2)/N;
    aic(I)        = N*(log(2*pi*sigma2_hat(I)) + 1) + 2*(I + 1);
end

結果. 選ばれたのは次数20で教科書と一緒なんやけど, どうも値が教科書の表5.1と違う. . .

name
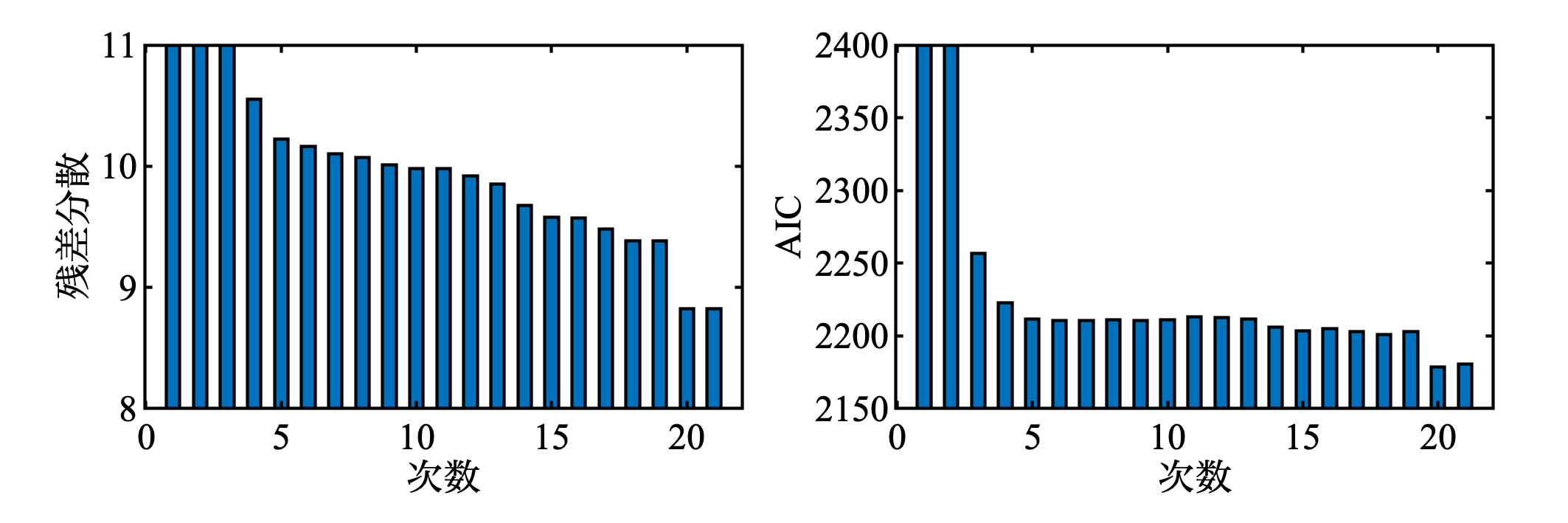
MATLABコード MATLAB 
t = tiledlayout(1, 2); t.Padding = 'compact'; t.TileSpacing = 'compact';
nexttile
bar(1:maxDeg, sigma2_hat, 0.5)
xlabel('次数')
ylabel('残差分散')
ylim([8 11])

nexttile
bar(1:maxDeg, aic, 0.5)
xlabel('次数')
ylabel('AIC')
ylim([2150 2400])

次数20の回帰曲線を描く. まあ, 合ってはいそう. しかし, 教科書とは少し形が違う.

name
MATLAB 
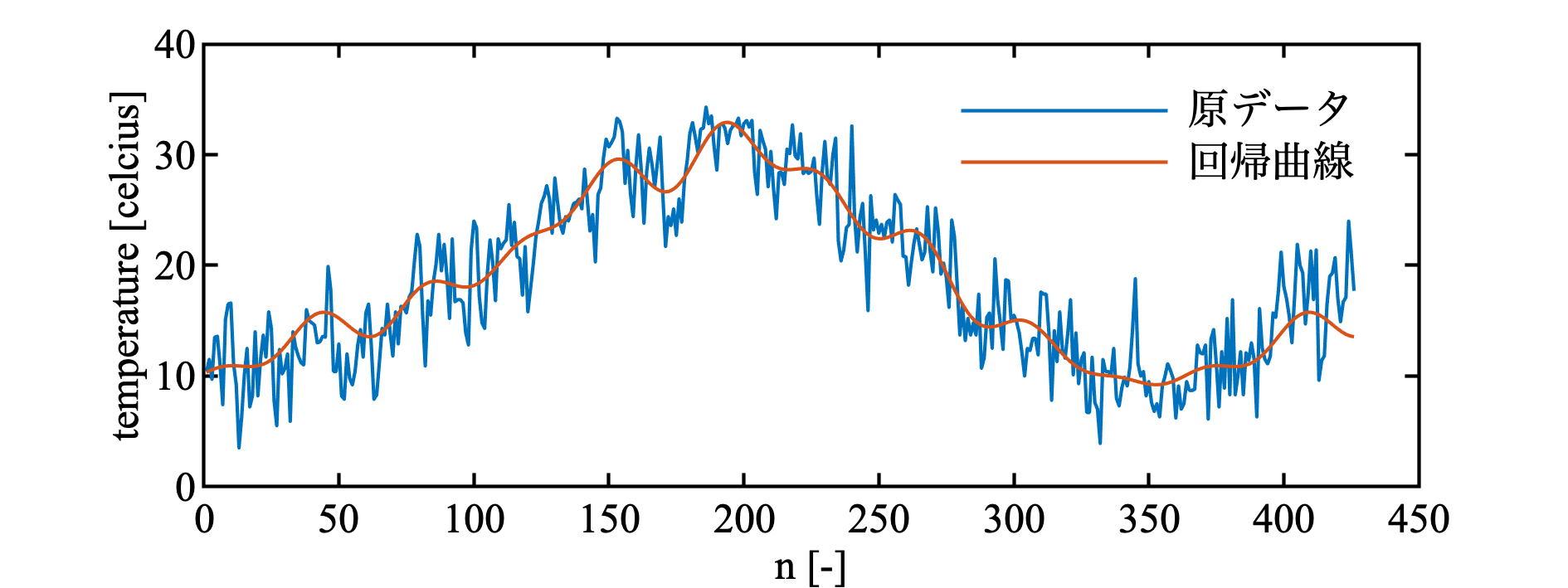
k = 20;

l = S(1:k, 1:k);
r = s(1:k);
param = l\r;
Zn     = Z(:, 1:k);
d_est = Zn * param;
plot([d_est d])

xlabel('n [-]');
ylabel('temperature [celcius]')
legend('原データ', '回帰曲線')

正規方程式を用いた検算

一応, 折角説明変数行列 $Z$ を作ったので, 正規方程式を用いて最尤推定量を求める. 正規方程式は, 僕の記事や, MATLAB公式の線形方程式のページに情報がある.

MATLAB 
k = 20;　           % 次数20を検討

Zn     = Z(:, 1:k); % 次数に合わせた説明変数行列を作る
param = Zn\d;       % 正規方程式を解く
d_est = Zn * param; 
s2    = sum((d - d_est).^2)/L
aicn  = N*(log(2*pi*s2) + 1) + 2*(k + 1)

推定分散 8.8217, AIC 2178.4 となり, ハウスホルダー法で求めた値も全くおなじになった. モデルのパラメータ推定値も全く同じになった ( よって回帰曲線も上と全く同じ ) .

主な参考文献


固有値計算と特異値計算 (計算力学レクチャーコース)

この記事のTOP    BACK    TOP